人教版七年级数学下册 5.3 平行线的性质 练习题(word版含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.3 平行线的性质 练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 12:39:00 | ||
图片预览

文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线
5.3平行线的性质 练习题
一、选择题
1.下列命题中,是假命题的是( )
A.在同一平面内,过一点有且只有一条直线与已知直线垂直
B.同旁内角互补,两直线平行
C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
D.过一点有且只有一条直线与已知直线平行
2.下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④如果两个角的两边分别平行,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
3.如果,直线,,则等于( )
A. B. C. D.
4.如图,,于点F,若,则( )
A. B. C. D.
5.如图,AB//CD,∠1+∠2=110°,则∠GEF+∠GFE的度数为( )
A.110° B.70° C.80° D.90°
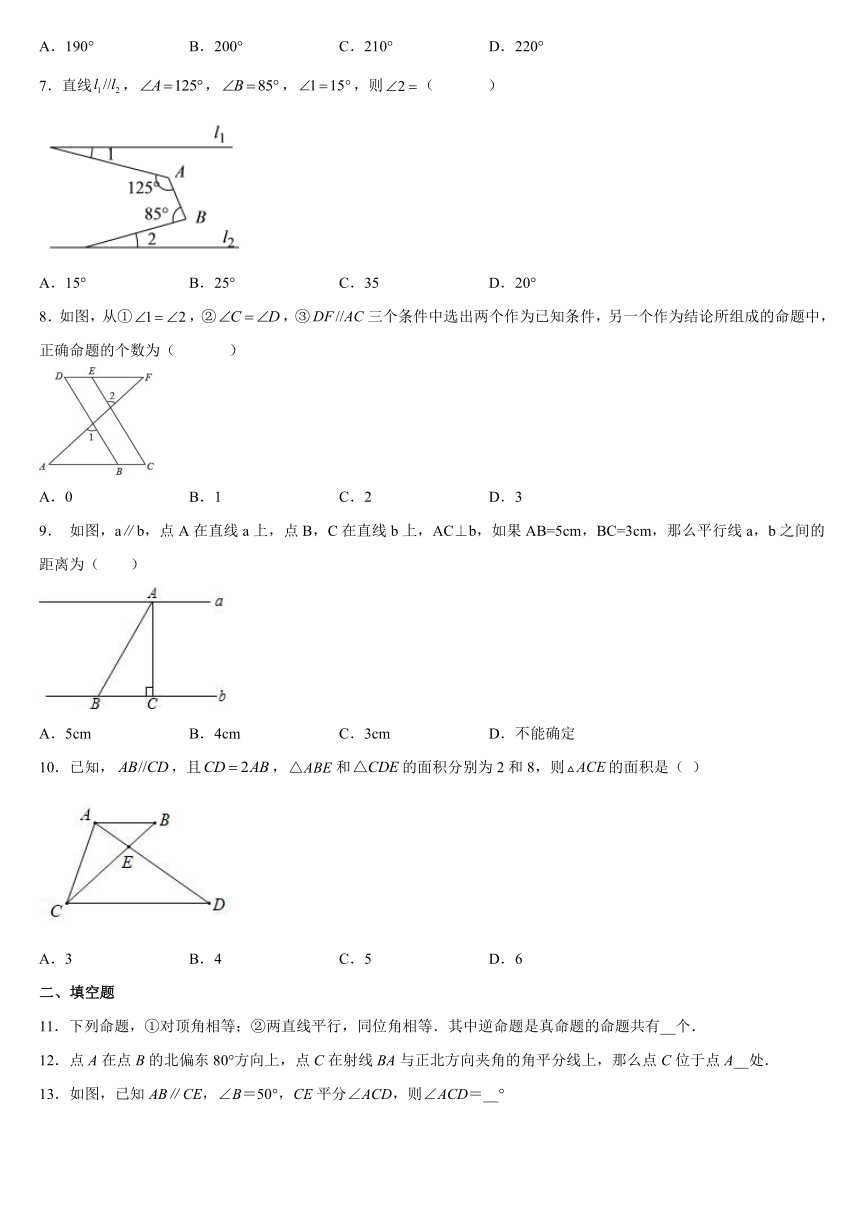
6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=( )
A.190° B.200° C.210° D.220°
7.直线,,,,则( )
A.15° B.25° C.35 D.20°
8.如图,从①,②,③三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
9. 如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
10.已知,,且,和的面积分别为2和8,则的面积是( )
A.3 B.4 C.5 D.6
二、填空题
11.下列命题,①对顶角相等;②两直线平行,同位角相等.其中逆命题是真命题的命题共有__个.
12.点A在点B的北偏东80°方向上,点C在射线BA与正北方向夹角的角平分线上,那么点C位于点A__处.
13.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD=__°
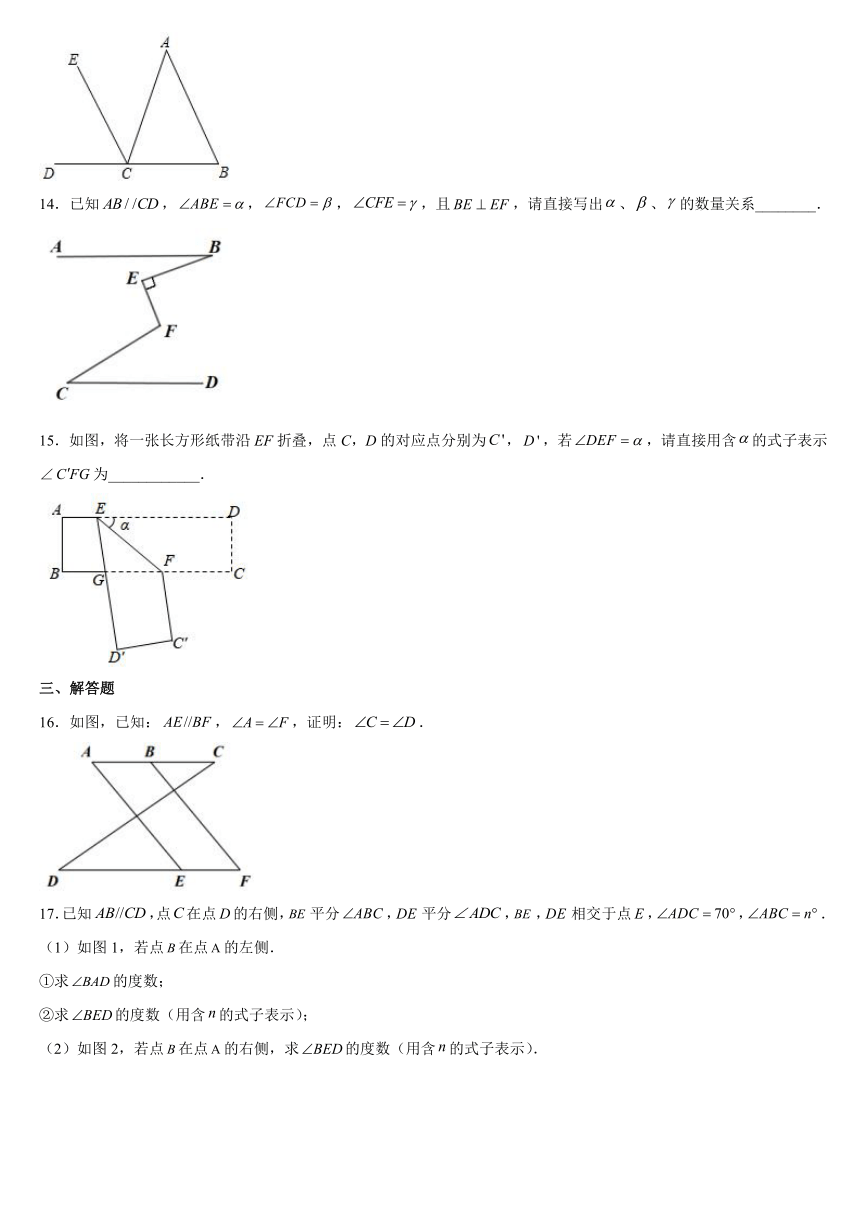
14.已知,,,,且,请直接写出、、的数量关系________.
15.如图,将一张长方形纸带沿EF折叠,点C,D的对应点分别为,,若,请直接用含的式子表示∠为____________.
三、解答题
16.如图,已知:,,证明:.
17.已知,点在点的右侧,平分,平分,,相交于点,,.
(1)如图1,若点在点的左侧.
①求的度数;
②求的度数(用含的式子表示);
(2)如图2,若点在点的右侧,求的度数(用含的式子表示).
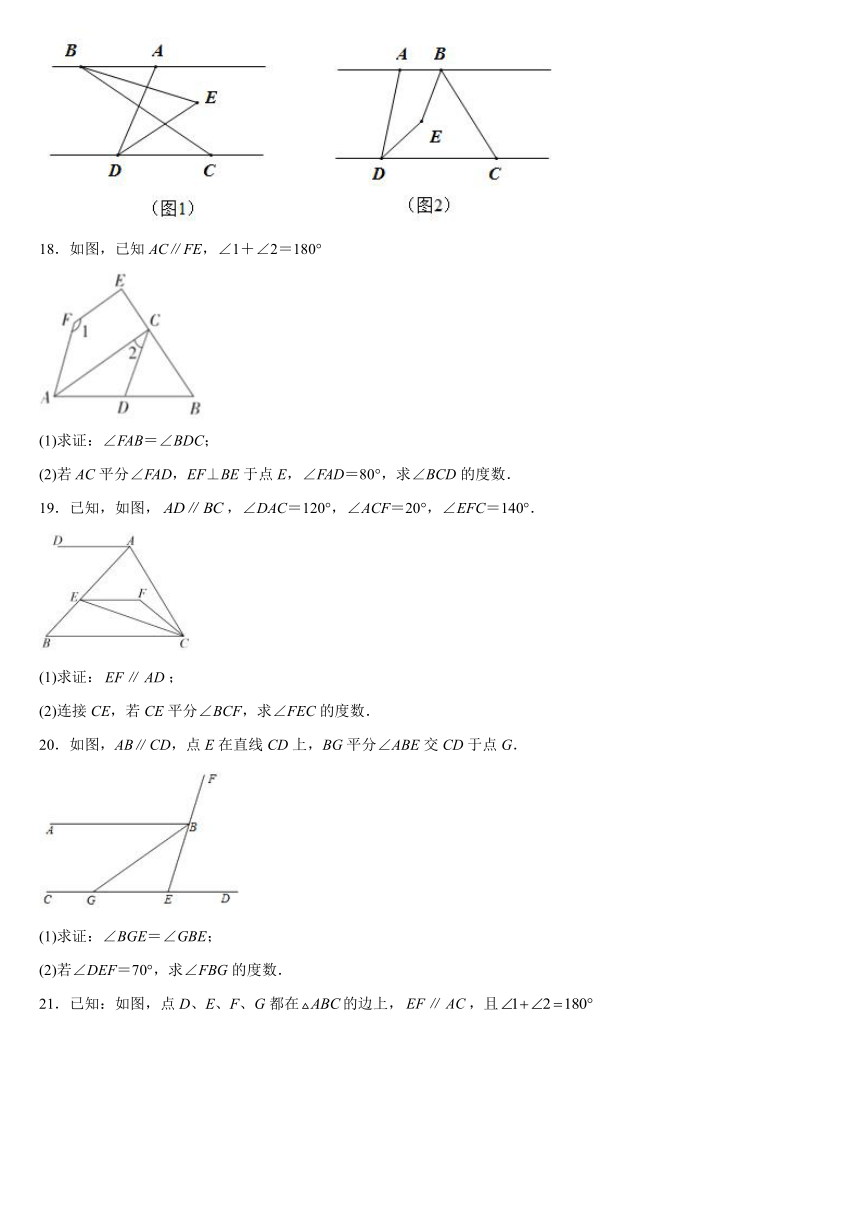
18.如图,已知AC∥FE,∠1+∠2=180°
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
19.已知,如图,,∠DAC=120°,∠ACF=20°,∠EFC=140°.
(1)求证:;
(2)连接CE,若CE平分∠BCF,求∠FEC的度数.
20.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
21.已知:如图,点D、E、F、G都在的边上,,且
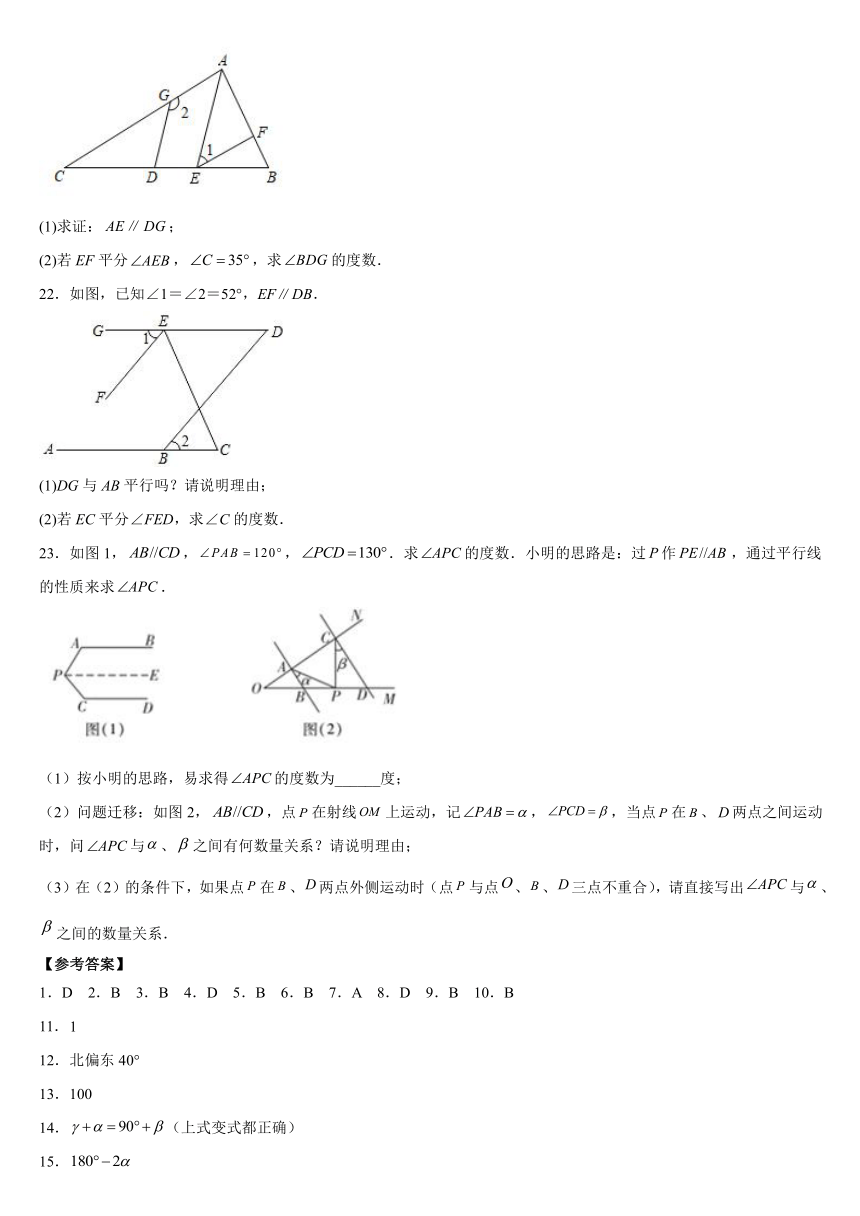
(1)求证:;
(2)若EF平分,,求的度数.
22.如图,已知∠1=∠2=52°,EFDB.
(1)DG与AB平行吗?请说明理由;
(2)若EC平分∠FED,求∠C的度数.
23.如图1,,,.求的度数.小明的思路是:过作,通过平行线的性质来求.
(1)按小明的思路,易求得的度数为______度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
【参考答案】
1.D 2.B 3.B 4.D 5.B 6.B 7.A 8.D 9.B 10.B
11.
12.北偏东40°
13.100
14.(上式变式都正确)
15.
16.证明:∵,
∴.
∵,
∴,
∴,
∴.
17.(1)①AB//CD,∠ADC=70°,
∴∠BAD=70°;
②如图1,过点E作EF//AB,
∵AB//CD,
∴AAB//CD//EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(2)如图2,过点E作EF//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB//CD,
∴AB//CD//EF,
∴∠BEF=180° ∠ABE=180° n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180° n°+35°=215° n°.
18.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°∠2=50°.
19.(1)证明:,
∠DAC+∠ACB=180°,
∠DAC=120°
∠ACB=60°,
∠ACF=20°,
∠BCF=60°-20°=40°,
∠EFC=140°,
∠BCF+∠EFC=180°,
;
(2)CE平分∠BCF,∠BCF=40°
∠BCE=∠ECF=20°
,
∠FEC=∠BCE=20°.
20.(1)证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
21.(1)解:证明:∵,
∴∠1=∠CAE,
∵∠1+∠2=180°,
∴∠2+∠CAE=180°,
∴;
(2)解:∵,∠C=35°,
∴∠BEF=∠C=35°,
∵EF平分∠AEB,
∴∠1=∠BEF=35°,
∴∠AEB=70°,
由(1)知,
∴∠BDG=∠AEB=70°.
22.(1)解: DG与AB平行.理由:
∵,
∴∠1=∠D.
∵∠1=∠2,
∴∠D=∠2.
∴.
(2)解:∵EC平分∠FED,
∴∠DEC=∠DEF.
∵∠1=50°,
∴∠DEF=180°﹣∠1=130°.
∴∠DEC=∠DEF=65°.
∵,
∴∠C=∠DEC=65°.
23.解:(1)∵AB∥CD,PE∥AB,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵,,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)
理由:过作交于,
∵,
∴
∴,,
∴;
(3)①当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
②当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
综上所述,
5.3平行线的性质 练习题
一、选择题
1.下列命题中,是假命题的是( )
A.在同一平面内,过一点有且只有一条直线与已知直线垂直
B.同旁内角互补,两直线平行
C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
D.过一点有且只有一条直线与已知直线平行
2.下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④如果两个角的两边分别平行,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
3.如果,直线,,则等于( )
A. B. C. D.
4.如图,,于点F,若,则( )
A. B. C. D.
5.如图,AB//CD,∠1+∠2=110°,则∠GEF+∠GFE的度数为( )
A.110° B.70° C.80° D.90°
6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=( )
A.190° B.200° C.210° D.220°
7.直线,,,,则( )
A.15° B.25° C.35 D.20°
8.如图,从①,②,③三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
9. 如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
10.已知,,且,和的面积分别为2和8,则的面积是( )
A.3 B.4 C.5 D.6
二、填空题
11.下列命题,①对顶角相等;②两直线平行,同位角相等.其中逆命题是真命题的命题共有__个.
12.点A在点B的北偏东80°方向上,点C在射线BA与正北方向夹角的角平分线上,那么点C位于点A__处.
13.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD=__°
14.已知,,,,且,请直接写出、、的数量关系________.
15.如图,将一张长方形纸带沿EF折叠,点C,D的对应点分别为,,若,请直接用含的式子表示∠为____________.
三、解答题
16.如图,已知:,,证明:.
17.已知,点在点的右侧,平分,平分,,相交于点,,.
(1)如图1,若点在点的左侧.
①求的度数;
②求的度数(用含的式子表示);
(2)如图2,若点在点的右侧,求的度数(用含的式子表示).
18.如图,已知AC∥FE,∠1+∠2=180°
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
19.已知,如图,,∠DAC=120°,∠ACF=20°,∠EFC=140°.
(1)求证:;
(2)连接CE,若CE平分∠BCF,求∠FEC的度数.
20.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
21.已知:如图,点D、E、F、G都在的边上,,且
(1)求证:;
(2)若EF平分,,求的度数.
22.如图,已知∠1=∠2=52°,EFDB.
(1)DG与AB平行吗?请说明理由;
(2)若EC平分∠FED,求∠C的度数.
23.如图1,,,.求的度数.小明的思路是:过作,通过平行线的性质来求.
(1)按小明的思路,易求得的度数为______度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
【参考答案】
1.D 2.B 3.B 4.D 5.B 6.B 7.A 8.D 9.B 10.B
11.
12.北偏东40°
13.100
14.(上式变式都正确)
15.
16.证明:∵,
∴.
∵,
∴,
∴,
∴.
17.(1)①AB//CD,∠ADC=70°,
∴∠BAD=70°;
②如图1,过点E作EF//AB,
∵AB//CD,
∴AAB//CD//EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(2)如图2,过点E作EF//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB//CD,
∴AB//CD//EF,
∴∠BEF=180° ∠ABE=180° n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180° n°+35°=215° n°.
18.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°∠2=50°.
19.(1)证明:,
∠DAC+∠ACB=180°,
∠DAC=120°
∠ACB=60°,
∠ACF=20°,
∠BCF=60°-20°=40°,
∠EFC=140°,
∠BCF+∠EFC=180°,
;
(2)CE平分∠BCF,∠BCF=40°
∠BCE=∠ECF=20°
,
∠FEC=∠BCE=20°.
20.(1)证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
21.(1)解:证明:∵,
∴∠1=∠CAE,
∵∠1+∠2=180°,
∴∠2+∠CAE=180°,
∴;
(2)解:∵,∠C=35°,
∴∠BEF=∠C=35°,
∵EF平分∠AEB,
∴∠1=∠BEF=35°,
∴∠AEB=70°,
由(1)知,
∴∠BDG=∠AEB=70°.
22.(1)解: DG与AB平行.理由:
∵,
∴∠1=∠D.
∵∠1=∠2,
∴∠D=∠2.
∴.
(2)解:∵EC平分∠FED,
∴∠DEC=∠DEF.
∵∠1=50°,
∴∠DEF=180°﹣∠1=130°.
∴∠DEC=∠DEF=65°.
∵,
∴∠C=∠DEC=65°.
23.解:(1)∵AB∥CD,PE∥AB,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵,,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)
理由:过作交于,
∵,
∴
∴,,
∴;
(3)①当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
②当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
综上所述,
