苏科版七年级数学下册第7章平面图形的认识(二) 单元综合达标测试题(word解析版)
文档属性
| 名称 | 苏科版七年级数学下册第7章平面图形的认识(二) 单元综合达标测试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 13:01:39 | ||
图片预览



文档简介
2021-2022学年苏科版七年级数学下册《第7章平面图形的认识(二)》
单元综合达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2.下列哪些图形是可以通过平移得到的( )
A. B.
C. D.
3.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
4.用下列多边形不能单独铺满地面的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
5.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
6.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDC=( )
A.120° B.60° C.140° D.无法确定
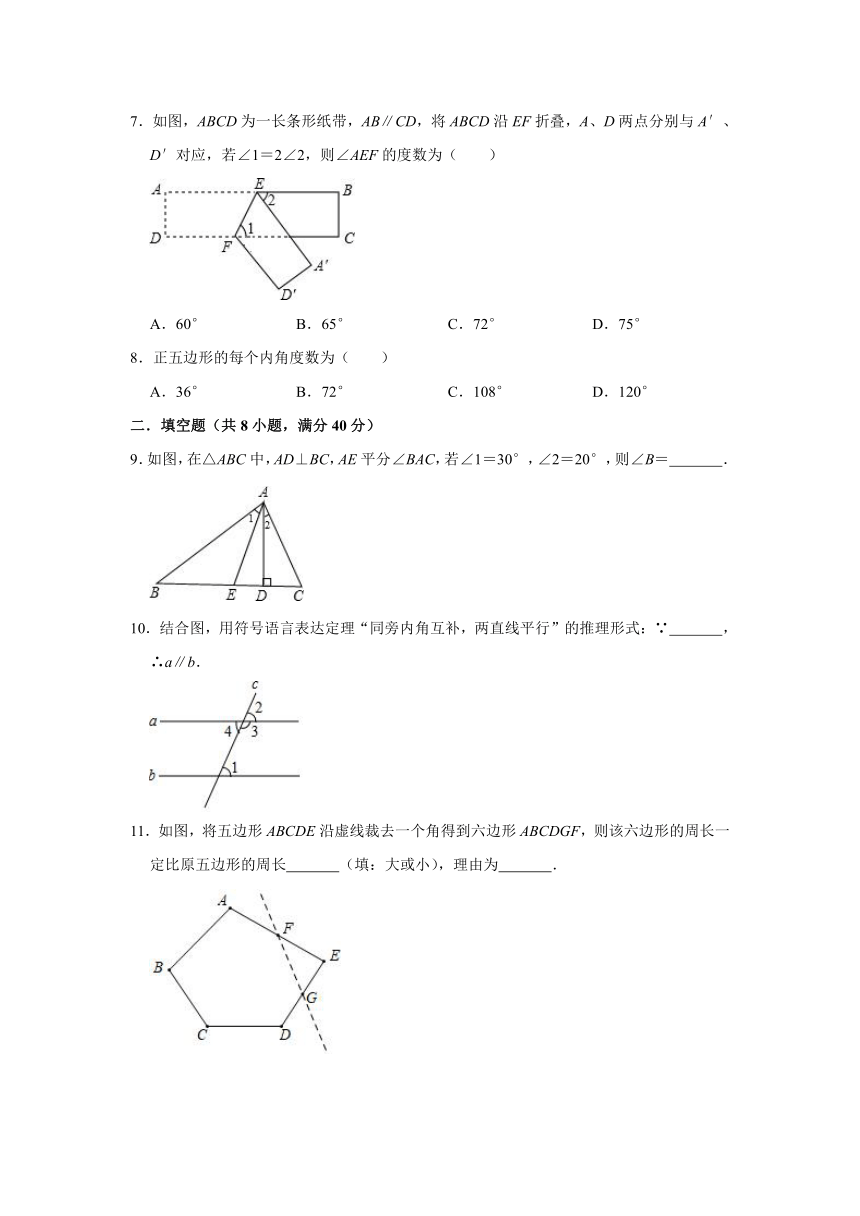
7.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60° B.65° C.72° D.75°
8.正五边形的每个内角度数为( )
A.36° B.72° C.108° D.120°
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
10.结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,∴a∥b.
11.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
12.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转.某一指令规定:机器人先向前行走1米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了 米.
13.小明家新建了一栋楼房,装修时准备在一段楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2m,其侧面如图所示,则铺设地毯至少需要 元.
14.已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .
15.如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 .
16.如图,已知∠1=∠2,∠B=35°,则∠3= .
三.解答题(共6小题,满分40分)
17.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
18.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
19.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=70°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求直线a与b的距离.
20.将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
(1)若∠DCE=45°,则∠ACB的度数为 ;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE之间存在什么数量关系?并说明理由;
(4)当∠ACE<90°且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出∠ACE的值;若不存在,请说明理由.
21.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数.
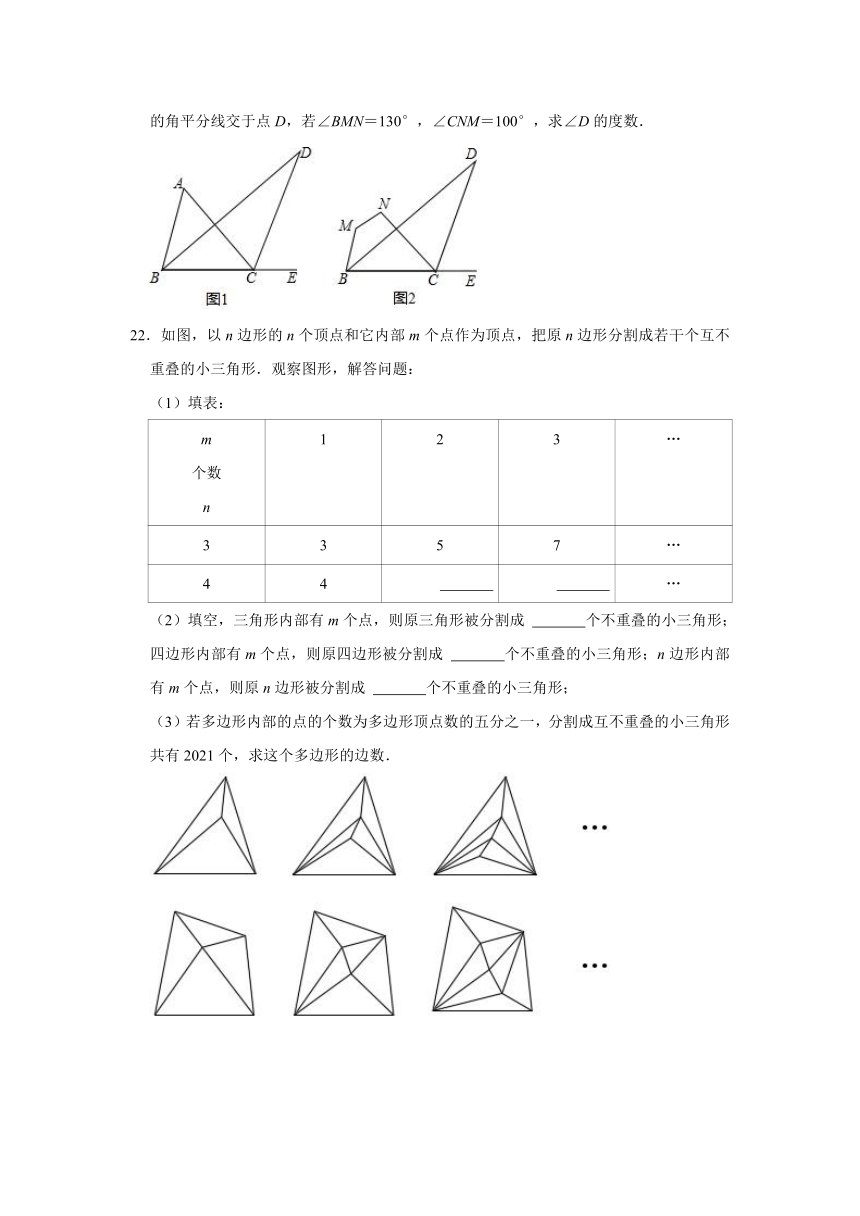
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE
的角平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
22.如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题:
(1)填表:
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 …
(2)填空,三角形内部有m个点,则原三角形被分割成 个不重叠的小三角形;四边形内部有m个点,则原四边形被分割成 个不重叠的小三角形;n边形内部有m个点,则原n边形被分割成 个不重叠的小三角形;
(3)若多边形内部的点的个数为多边形顶点数的五分之一,分割成互不重叠的小三角形共有2021个,求这个多边形的边数.
参考答案
一.选择题(共8小题,满分40分)
1.解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
2.解:A、通过旋转得到,故本选项错误;
B、通过平移得到,故本选项正确;
C、通过轴对称得到,故本选项错误;
D、通过旋转得到,故本选项错误.
故选:B.
3.解:对角线的数量m=6﹣3=3条;
分成的三角形的数量为n=6﹣2=4个.
故选:C.
4.解:A.正三角形每个内角为60°,能整除360°,所以能铺满地面;
B.正四边形每个内角为90°,能整除360°,所以能铺满地面;
C.正六边形每个内角为120°,能整除360°,所以能铺满地面;
D.正八边形每个内角为135°,不能整除360°,所以不能铺满地面;
故选:D.
5.解:根据同位角的定义可知D选项中∠1与∠2在直线的同侧,并且在第三条直线(截线)的同旁,故是同位角.
故选:D.
6.解:在△ABC中,∵∠A=120°,
∴∠ABC+∠ACB=180°﹣120°=60°,
又∵∠1=∠2=∠3,∠4=∠5=∠6,
∴∠DBC+∠DCB=×60°=40°,
∴∠BDC=180°﹣40°=140°,
故选:C.
7.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
8.解:正五边形的每个外角==72°,
∴正五边形的每个内角=180°﹣72°=108°,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
10.解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故答案为:∠1+∠3=180°.
11.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
12.解:机器人转了一周共360度,360°÷45°=8,共走了8次,机器人走了8×1=8米.
13.解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为3米,2.5米,
则地毯的长度为3+2.5=5.5(米),面积为5.5×2=11(m2),
故买地毯至少需要11×50=550(元).
故答案为:550.
14.解:∵△ABC的三边长分别是a、b、c,
∴a+b>c,b﹣a<c,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣(﹣b+a+c)=a+b﹣c+b﹣a﹣c=2b﹣2c;
故答案为:2b﹣2c
15.解:如图,
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
故答案为:140°.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠B,
∵∠B=35°,
∴∠3=35°.
故答案为35°.
三.解答题(共6小题,满分40分)
17.证明一:∵∠A=∠1,
∴AE∥BF,
∴∠2=∠E.
∵CE∥DF,
∴∠2=∠F,
∴∠E=∠F.
证明二:∵CE∥DF,
∴∠ACE=∠D,
∵∠A=∠1,
∴180°﹣∠ACE﹣∠A=180°﹣∠D﹣∠1,
又∵∠E=180°﹣∠ACE﹣∠A,∠F=180°﹣∠D﹣∠1,
∴∠E=∠F.
18.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
19.解:(1)∵a∥b,
∴∠3=∠1=70°,
∵AC⊥AB,
∴∠2+∠3=90°,
∴∠2=90°﹣70°=20°.
答:∠2的度数为20°;
(2)∵AC=3,AB=4,BC=5,
设直线a与b的距离为h,
∴S△ABC=AC×AB=BC×h,
即5h=3×4,
∴h=.
答:直线a与b的距离为.
20.解:(1)∵∠DCE=45°,∠ACD=90°
∴∠ACE=45°
∵∠BCE=90°
∴∠ACB=90°+45°=135°
故答案为:135°;
(2)∵∠ACB=140°,∠ECB=90°
∴∠ACE=140°﹣90°=50°
∴∠DCE=90°﹣∠ACE=90°﹣50°=40°;
(3)猜想:∠ACB+∠DCE=180°
理由如下:∵∠ACE=90°﹣∠DCE
又∵∠ACB=∠ACE+90°
∴∠ACB=90°﹣∠DCE+90°=180°﹣∠DCE
即∠ACB+∠DCE=180°;
(4)30°;
理由:∵∠ACD=∠ECB=90°,
∴∠ACE=∠DCB=30°,
∴∠D=∠DCB=30°,
∴CB∥AD.
21.解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴,.
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D,
∴=,即,
∴.
∵∠ABC=75°,∠ACB=45°,∠A=60°,
∴∠D=30°.
(2)如图,延长BM,CN交于点A.
∵∠BMN=∠ANM+∠A,∠CNM=∠AMN+∠A,
∴∠A=∠BMN+∠CNM﹣180°=50°,
由(1)知.
22.解:(1)观察图形,完成下表,
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 6 8 …
故答案为:6,8;
(2)三角形内部1个点时,共分割成3部分,3=3+2(1﹣1),
三角形内部2个点时,共分割成5部分,5=3+2(2﹣1),
三角形内部3个点时,共分割成7部分,7=3+2(3﹣1),
…,
所以,三角形内部有m个点时,3+2(m﹣1)=2m+1,
四边形的4个顶点和它内部的m个点,
则分割成的不重叠的三角形的个数为:4+2(m﹣1)=2m+2,
n边形内部有m个点,则原n边形被分割成n+2(m﹣1)=2m+n﹣2个不重叠的小三角形;
故答案为:(2m+1),(2m+2),(2m+n﹣2);
(3)设这个多边形的边数为n,则内部的点的个数为n,
根据题意得,2×n+n﹣2=2021,
解得:n=1445,
答:这个多边形的边数为1445.
单元综合达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2.下列哪些图形是可以通过平移得到的( )
A. B.
C. D.
3.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
4.用下列多边形不能单独铺满地面的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
5.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
6.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDC=( )
A.120° B.60° C.140° D.无法确定
7.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60° B.65° C.72° D.75°
8.正五边形的每个内角度数为( )
A.36° B.72° C.108° D.120°
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
10.结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,∴a∥b.
11.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
12.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转.某一指令规定:机器人先向前行走1米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了 米.
13.小明家新建了一栋楼房,装修时准备在一段楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2m,其侧面如图所示,则铺设地毯至少需要 元.
14.已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .
15.如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 .
16.如图,已知∠1=∠2,∠B=35°,则∠3= .
三.解答题(共6小题,满分40分)
17.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
18.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
19.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=70°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求直线a与b的距离.
20.将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
(1)若∠DCE=45°,则∠ACB的度数为 ;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE之间存在什么数量关系?并说明理由;
(4)当∠ACE<90°且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出∠ACE的值;若不存在,请说明理由.
21.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数.
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE
的角平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
22.如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题:
(1)填表:
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 …
(2)填空,三角形内部有m个点,则原三角形被分割成 个不重叠的小三角形;四边形内部有m个点,则原四边形被分割成 个不重叠的小三角形;n边形内部有m个点,则原n边形被分割成 个不重叠的小三角形;
(3)若多边形内部的点的个数为多边形顶点数的五分之一,分割成互不重叠的小三角形共有2021个,求这个多边形的边数.
参考答案
一.选择题(共8小题,满分40分)
1.解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
2.解:A、通过旋转得到,故本选项错误;
B、通过平移得到,故本选项正确;
C、通过轴对称得到,故本选项错误;
D、通过旋转得到,故本选项错误.
故选:B.
3.解:对角线的数量m=6﹣3=3条;
分成的三角形的数量为n=6﹣2=4个.
故选:C.
4.解:A.正三角形每个内角为60°,能整除360°,所以能铺满地面;
B.正四边形每个内角为90°,能整除360°,所以能铺满地面;
C.正六边形每个内角为120°,能整除360°,所以能铺满地面;
D.正八边形每个内角为135°,不能整除360°,所以不能铺满地面;
故选:D.
5.解:根据同位角的定义可知D选项中∠1与∠2在直线的同侧,并且在第三条直线(截线)的同旁,故是同位角.
故选:D.
6.解:在△ABC中,∵∠A=120°,
∴∠ABC+∠ACB=180°﹣120°=60°,
又∵∠1=∠2=∠3,∠4=∠5=∠6,
∴∠DBC+∠DCB=×60°=40°,
∴∠BDC=180°﹣40°=140°,
故选:C.
7.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
8.解:正五边形的每个外角==72°,
∴正五边形的每个内角=180°﹣72°=108°,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
10.解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故答案为:∠1+∠3=180°.
11.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
12.解:机器人转了一周共360度,360°÷45°=8,共走了8次,机器人走了8×1=8米.
13.解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为3米,2.5米,
则地毯的长度为3+2.5=5.5(米),面积为5.5×2=11(m2),
故买地毯至少需要11×50=550(元).
故答案为:550.
14.解:∵△ABC的三边长分别是a、b、c,
∴a+b>c,b﹣a<c,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣(﹣b+a+c)=a+b﹣c+b﹣a﹣c=2b﹣2c;
故答案为:2b﹣2c
15.解:如图,
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
故答案为:140°.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠B,
∵∠B=35°,
∴∠3=35°.
故答案为35°.
三.解答题(共6小题,满分40分)
17.证明一:∵∠A=∠1,
∴AE∥BF,
∴∠2=∠E.
∵CE∥DF,
∴∠2=∠F,
∴∠E=∠F.
证明二:∵CE∥DF,
∴∠ACE=∠D,
∵∠A=∠1,
∴180°﹣∠ACE﹣∠A=180°﹣∠D﹣∠1,
又∵∠E=180°﹣∠ACE﹣∠A,∠F=180°﹣∠D﹣∠1,
∴∠E=∠F.
18.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
19.解:(1)∵a∥b,
∴∠3=∠1=70°,
∵AC⊥AB,
∴∠2+∠3=90°,
∴∠2=90°﹣70°=20°.
答:∠2的度数为20°;
(2)∵AC=3,AB=4,BC=5,
设直线a与b的距离为h,
∴S△ABC=AC×AB=BC×h,
即5h=3×4,
∴h=.
答:直线a与b的距离为.
20.解:(1)∵∠DCE=45°,∠ACD=90°
∴∠ACE=45°
∵∠BCE=90°
∴∠ACB=90°+45°=135°
故答案为:135°;
(2)∵∠ACB=140°,∠ECB=90°
∴∠ACE=140°﹣90°=50°
∴∠DCE=90°﹣∠ACE=90°﹣50°=40°;
(3)猜想:∠ACB+∠DCE=180°
理由如下:∵∠ACE=90°﹣∠DCE
又∵∠ACB=∠ACE+90°
∴∠ACB=90°﹣∠DCE+90°=180°﹣∠DCE
即∠ACB+∠DCE=180°;
(4)30°;
理由:∵∠ACD=∠ECB=90°,
∴∠ACE=∠DCB=30°,
∴∠D=∠DCB=30°,
∴CB∥AD.
21.解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴,.
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D,
∴=,即,
∴.
∵∠ABC=75°,∠ACB=45°,∠A=60°,
∴∠D=30°.
(2)如图,延长BM,CN交于点A.
∵∠BMN=∠ANM+∠A,∠CNM=∠AMN+∠A,
∴∠A=∠BMN+∠CNM﹣180°=50°,
由(1)知.
22.解:(1)观察图形,完成下表,
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 6 8 …
故答案为:6,8;
(2)三角形内部1个点时,共分割成3部分,3=3+2(1﹣1),
三角形内部2个点时,共分割成5部分,5=3+2(2﹣1),
三角形内部3个点时,共分割成7部分,7=3+2(3﹣1),
…,
所以,三角形内部有m个点时,3+2(m﹣1)=2m+1,
四边形的4个顶点和它内部的m个点,
则分割成的不重叠的三角形的个数为:4+2(m﹣1)=2m+2,
n边形内部有m个点,则原n边形被分割成n+2(m﹣1)=2m+n﹣2个不重叠的小三角形;
故答案为:(2m+1),(2m+2),(2m+n﹣2);
(3)设这个多边形的边数为n,则内部的点的个数为n,
根据题意得,2×n+n﹣2=2021,
解得:n=1445,
答:这个多边形的边数为1445.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
