福建省三明市富兴中学2013届高三第三次月考数学(文)试题
文档属性
| 名称 | 福建省三明市富兴中学2013届高三第三次月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-29 00:00:00 | ||
图片预览



文档简介
三明市富兴中学2013届高三第三次月考试题
数学文科试卷
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个项符合题目要求,请把正确选项的代号填在答题卷相应的位置上)
1.已知全集U=R,集合A={x|},B={x|},则?CR等于( )
A. B.
C. D.
2.i是虚数单位,若iR),则ab的值是 … ( )
A.-15 B.-3 C.3 D.15
3. 函数的定义域为( )
A. B. C. D.
4.设是平面内两条不同的直线,是平面外的一条直线,则“,”是“”的( )
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
5.为了了解某校高三400名学生的数学学业水平测试成绩,
制成样本频率分布直方图如图1,规定不低于60分为及格,
不低于80分为优秀,则及格率与优秀人数分别是( )
A.60%,60 B.60%,80 C.80%,80 D.80%,60
图1
6.在独立性检验中,统计量有两个临界值:3.841和6.635;当>3.841时,有95%的把握说明两个事件有关,当>6.635时,有99%的把握说明两个事件有关,当3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的=20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
A.有95%的把握认为两者有关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
7.由代数式的乘法法则类比推导向量的数量积的运算法则?:
①“mn=nm”类比得到“ab=ba”;
②“(m+n)t=mt+nt”类比得到“(a+b) c=ac+bc”;
③“”类比得到“(ab)c=a(bc)”;
④“”类比得到“p0, a p=xpa=x”;
⑤“||=|m||n|”类比得到“| ab |=|a||b|?”;
以上式子中,类比得到的结论正确的个数是( )
A.1 B.2
C.3 D.4
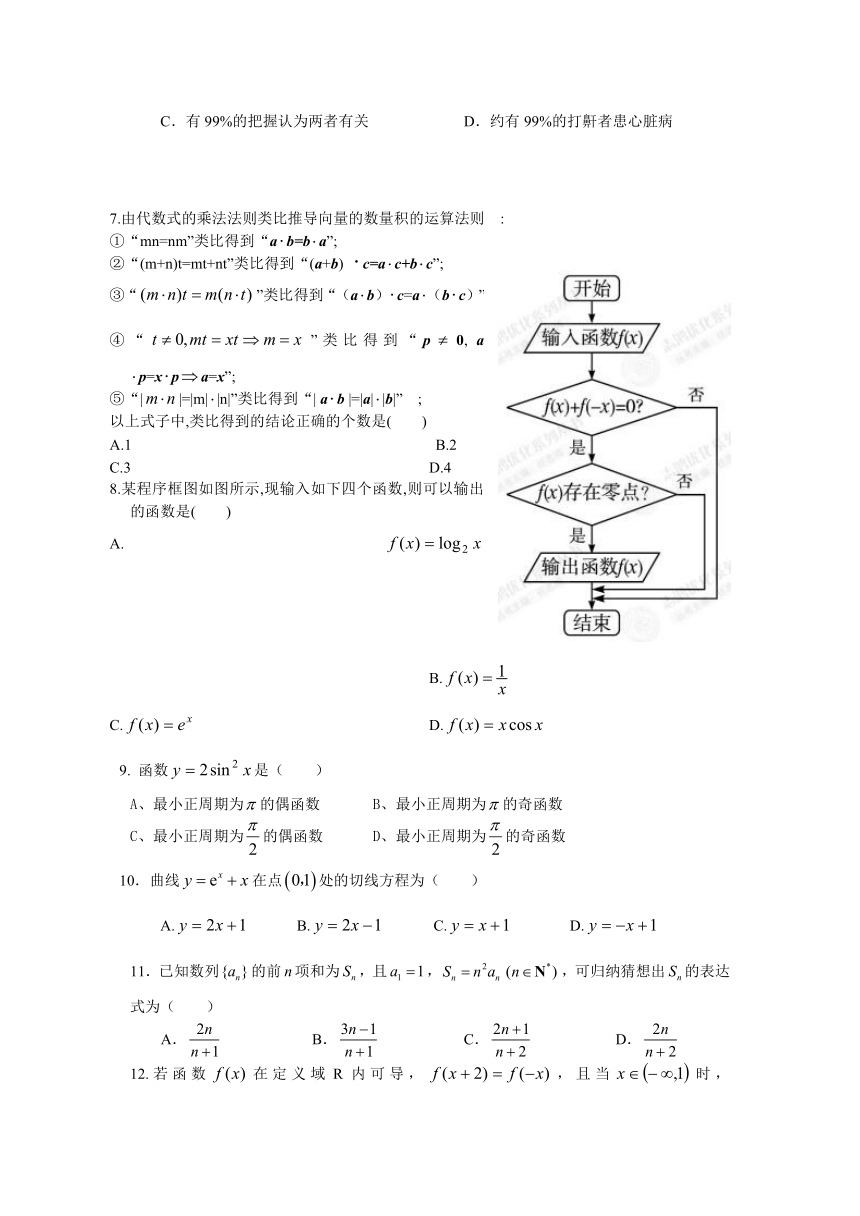
8.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. B.
C. D.
9. 函数是( )
A、最小正周期为的偶函数 B、最小正周期为的奇函数
C、最小正周期为的偶函数 D、最小正周期为的奇函数
10.曲线在点处的切线方程为( )
A. B. C. D.
11.已知数列的前项和为,且,,可归纳猜想出的表达式为( )
A. B. C. D.
12.若函数在定义域R内可导,,且当时,,设则( )
A. B. C. D.
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分.把正确答案直接写在答题卷相应位置上)
13. 某小卖部为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯
数与当天气温,并制作了对照表:
由表中数据算得线性回归方程中的预测当气温为-5 ℃时,热茶销售量
为 杯.
14.已知函数是的导函数,且是偶函数,则的递增区间是
15.已知,若有两个元素,则的取值范围是
16.在平面直角坐标系中,的顶点、分别是离心率为的圆锥曲线的焦点,顶点在该曲线上.一同学已正确地推得:当时,有.类似地,当、时,有 .
三、解答题(本大题共6题,共74分.解答应写出文字说明,证明推理过程或演算步骤)
17.(本小题满分12分)
设数列的前项和为,且满足.
(Ⅰ)求,,,的值并猜想其通项公式;
(Ⅱ)用三段论证明数列是等比数列.
18. (本小题满分12分)已知△的内角的对边分别为,其中,向量m,n,m·n=1.(1)若,求的值;(2)若,求△的面积.
19.(本小题满分12分)
已知关于的一元二次函数
(Ⅰ)设集合和,分别从集合和中随机取一个数作为和,求函数在区间[上是增函数的概率;
(Ⅱ)设点是区域内的随机点,
记有两个零点,其中一个大于,另一个小于,求事件发生的概率.
20. (本小题满分12分)如图,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
21.(本小题满分12分)
设函数为实数。
(Ⅰ)已知函数在处取得极值,求的值;
(Ⅱ)已知不等式对任意都成立,求实数的取值范围。
22.(本小题满分14分)已知椭圆的一个焦点为,与两坐标轴正半轴分别交于A,B两点(如图),向量与向量m共线.
(1)求椭圆的方程;
(2)若斜率为k的直线过点C(0,2),且与椭圆交于P,Q两点,求△POC与△QOC面积之比的取值范围.
2012-2013学年第一学期第三次月考
高三数学文科试卷答案
19
则事件包含基本事件的个数是1+2+2=5,∴……6分
(Ⅱ)依条件可知试验的全部结果所构成的区域为,
其面积 ……………………………………8分
事件构成的区域:
由,得交点坐标为………………………………10分
,∴事件发生的概率为 ……12分
20【解】(1)取CD的中点G,连接MG,NG. …………1分
设正方形ABCD,DCEF的边长为2,
则. …………2分
因为平面平面DCEF,
所以平面DCEF. …………3分
可得是MN与平面DCEF所成的角. …………4分
因为
所以sin…………5分
即MN与平面DCEF所成角的正弦值为. …………6分
(2)证明:假设直线ME与BN共面, …………7分
则平面MBEN,且平面MBEN与平面DCEF交于EN.
由已知,两正方形不共面,故平面DCEF.
又AB∥CD,所以AB∥平面DCEF. …………9分
而EN为平面MBEN与平面DCEF的交线,所以AB∥EN. …………10分
又AB∥CD∥EF,所以EN∥EF,这与矛盾,故假设不成立. …………11分
所以直线ME与BN不共面,即它们是异面直线. …………12分
22【解】(1)由向量与向量m共线,可得
又所以.
所以椭圆方程为. …………4分
(2)设且.
PQ方程为y=kx+2,代入椭圆方程并消去y,
得 …………5分
所以 ①
数学文科试卷
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个项符合题目要求,请把正确选项的代号填在答题卷相应的位置上)
1.已知全集U=R,集合A={x|},B={x|},则?CR等于( )
A. B.
C. D.
2.i是虚数单位,若iR),则ab的值是 … ( )
A.-15 B.-3 C.3 D.15
3. 函数的定义域为( )
A. B. C. D.
4.设是平面内两条不同的直线,是平面外的一条直线,则“,”是“”的( )
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
5.为了了解某校高三400名学生的数学学业水平测试成绩,
制成样本频率分布直方图如图1,规定不低于60分为及格,
不低于80分为优秀,则及格率与优秀人数分别是( )
A.60%,60 B.60%,80 C.80%,80 D.80%,60
图1
6.在独立性检验中,统计量有两个临界值:3.841和6.635;当>3.841时,有95%的把握说明两个事件有关,当>6.635时,有99%的把握说明两个事件有关,当3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的=20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
A.有95%的把握认为两者有关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
7.由代数式的乘法法则类比推导向量的数量积的运算法则?:
①“mn=nm”类比得到“ab=ba”;
②“(m+n)t=mt+nt”类比得到“(a+b) c=ac+bc”;
③“”类比得到“(ab)c=a(bc)”;
④“”类比得到“p0, a p=xpa=x”;
⑤“||=|m||n|”类比得到“| ab |=|a||b|?”;
以上式子中,类比得到的结论正确的个数是( )
A.1 B.2
C.3 D.4
8.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. B.
C. D.
9. 函数是( )
A、最小正周期为的偶函数 B、最小正周期为的奇函数
C、最小正周期为的偶函数 D、最小正周期为的奇函数
10.曲线在点处的切线方程为( )
A. B. C. D.
11.已知数列的前项和为,且,,可归纳猜想出的表达式为( )
A. B. C. D.
12.若函数在定义域R内可导,,且当时,,设则( )
A. B. C. D.
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分.把正确答案直接写在答题卷相应位置上)
13. 某小卖部为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯
数与当天气温,并制作了对照表:
由表中数据算得线性回归方程中的预测当气温为-5 ℃时,热茶销售量
为 杯.
14.已知函数是的导函数,且是偶函数,则的递增区间是
15.已知,若有两个元素,则的取值范围是
16.在平面直角坐标系中,的顶点、分别是离心率为的圆锥曲线的焦点,顶点在该曲线上.一同学已正确地推得:当时,有.类似地,当、时,有 .
三、解答题(本大题共6题,共74分.解答应写出文字说明,证明推理过程或演算步骤)
17.(本小题满分12分)
设数列的前项和为,且满足.
(Ⅰ)求,,,的值并猜想其通项公式;
(Ⅱ)用三段论证明数列是等比数列.
18. (本小题满分12分)已知△的内角的对边分别为,其中,向量m,n,m·n=1.(1)若,求的值;(2)若,求△的面积.
19.(本小题满分12分)
已知关于的一元二次函数
(Ⅰ)设集合和,分别从集合和中随机取一个数作为和,求函数在区间[上是增函数的概率;
(Ⅱ)设点是区域内的随机点,
记有两个零点,其中一个大于,另一个小于,求事件发生的概率.
20. (本小题满分12分)如图,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
21.(本小题满分12分)
设函数为实数。
(Ⅰ)已知函数在处取得极值,求的值;
(Ⅱ)已知不等式对任意都成立,求实数的取值范围。
22.(本小题满分14分)已知椭圆的一个焦点为,与两坐标轴正半轴分别交于A,B两点(如图),向量与向量m共线.
(1)求椭圆的方程;
(2)若斜率为k的直线过点C(0,2),且与椭圆交于P,Q两点,求△POC与△QOC面积之比的取值范围.
2012-2013学年第一学期第三次月考
高三数学文科试卷答案
19
则事件包含基本事件的个数是1+2+2=5,∴……6分
(Ⅱ)依条件可知试验的全部结果所构成的区域为,
其面积 ……………………………………8分
事件构成的区域:
由,得交点坐标为………………………………10分
,∴事件发生的概率为 ……12分
20【解】(1)取CD的中点G,连接MG,NG. …………1分
设正方形ABCD,DCEF的边长为2,
则. …………2分
因为平面平面DCEF,
所以平面DCEF. …………3分
可得是MN与平面DCEF所成的角. …………4分
因为
所以sin…………5分
即MN与平面DCEF所成角的正弦值为. …………6分
(2)证明:假设直线ME与BN共面, …………7分
则平面MBEN,且平面MBEN与平面DCEF交于EN.
由已知,两正方形不共面,故平面DCEF.
又AB∥CD,所以AB∥平面DCEF. …………9分
而EN为平面MBEN与平面DCEF的交线,所以AB∥EN. …………10分
又AB∥CD∥EF,所以EN∥EF,这与矛盾,故假设不成立. …………11分
所以直线ME与BN不共面,即它们是异面直线. …………12分
22【解】(1)由向量与向量m共线,可得
又所以.
所以椭圆方程为. …………4分
(2)设且.
PQ方程为y=kx+2,代入椭圆方程并消去y,
得 …………5分
所以 ①
同课章节目录
