16.2 二次根式的乘法 第1课时 课件(共28张PPT)
文档属性
| 名称 | 16.2 二次根式的乘法 第1课时 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 13:05:36 | ||
图片预览





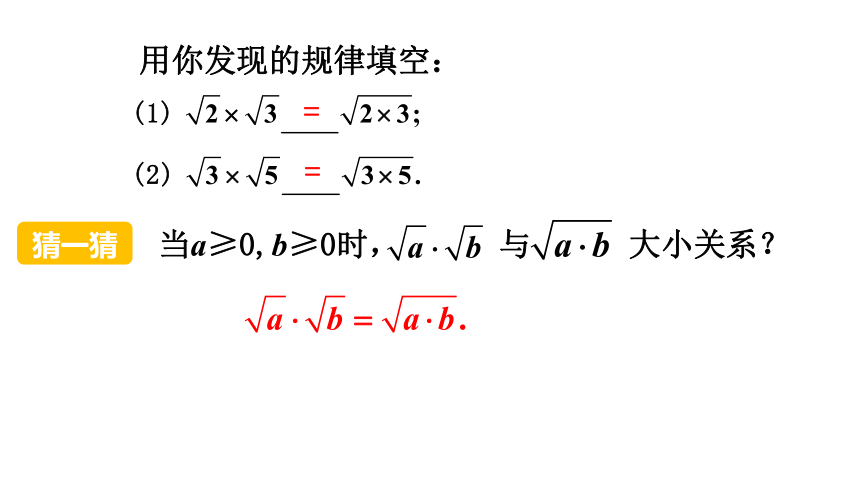


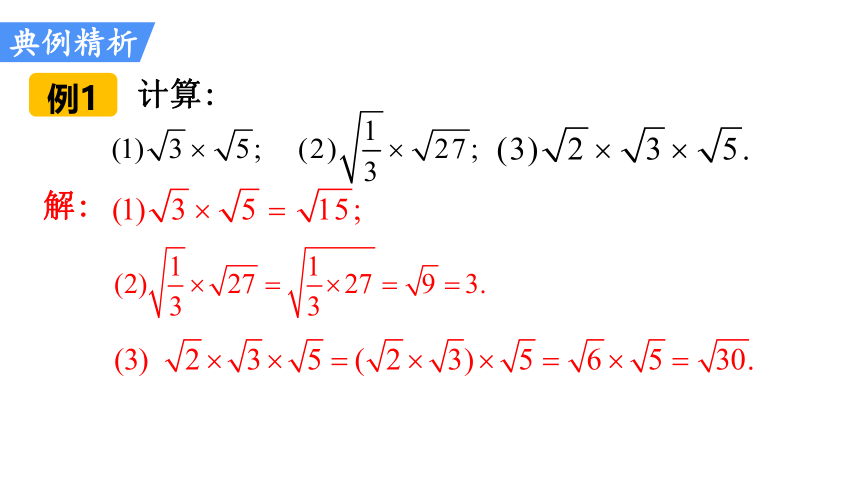
文档简介
(共28张PPT)
2022年春人教版数学
八年级下册数学精品课件
16.2 二根次式的乘除
第1课时 二次根式的乘法
第十六章 二次根式
情境引入
1.理解二次根式的乘法法则及积的算术平方根的性质.(重点)
2.合理简洁地进行二次根式的乘法运算.(难点)
学习目标
下面是意大利艺术家列奥纳多·达·芬奇所创作世界名画,请根据不同的已知条件,分别表示出它的面积.
(1)当长为2m,宽为3n,则面积S= ;
(2)当长为 , 宽为 时,则S= ;
6mn
你知道这是什么运算?又如何进行计算呢?
导入新课
二次根式的乘法
1.计算下列各式:
6
6
20
20
30
30
观察计算结果,你发现什么规律?
一
讲授新课
用你发现的规律填空:
当a≥0,b≥0时, 与 大小关系?
=
=
猜一猜
根据积的乘方法则,有
所以
就是ab算术平方根.
而 表示ab算术平方根.
即
证一证
二次根式的乘法法则
首页
文字叙述
算术平方根的乘积等于各个被开方数积的算术平方根.
a,b都必须是非负数.
归纳总结
要点提醒
计算:
解:
例1
纳
典例精析
(1)(2)属于两个二次根式的乘法,按照法则进行计算即可;(3)只需其中两个结合就可实现转化进行计算.(3)说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即 .
归纳
试回顾如何计算3a2·2a3= .
还记得单项式乘以单项式的法则吗?
如何计算呢?
6a5
解:
形如 的乘法
二
想一想
二次根式的乘法扩充法则
第一步:根号外的系数与系数相乘,积为结果的系数;
第二步:根式和根式按公式相乘.
利用它可以进行二次根式的化简.
归纳总结
积的算术平方根的性质及应用
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
在本章中,如果没有特别说明,所有的字母都表示正数.
这个性质在有的地方称之为“积的算术平方根的性质”
三
解:(1) ;
计算:
(1) ;(2) .
(2)
例2
计算:
(1) ;(2) ;(3) .
解:(1)
(2)
(3)
例3
在化简 时,小明是这样进行的:
解:
假如你是他的数学老师,你认为他做对了吗?为什么?如果不对,请改正过来!
答:不对.被开方数的两个因数是负数,不能直接套用积的算术平方根的性质.
正确解法:
议一议
在使用上述积的算术平方根的性质进行计算时,一定要注意前提条件即被开方数的每个因数都必须为非负数.对于不能直接用的,一定要先进行适当转化.
要点提醒
现在你能用上面的性质说明 吗?
抢答游戏:
将从1至100的非平方数的算术平方根的结果快速说出来.竞赛方法:1.四人一组;2.一人报数,一人评判并记录;3.两位同学抢答结果,此为第一轮比赛结果;4.胜者与第三人按同样的方法;5.最后决出本小组的冠军;6.本小组成员用掌声祝贺冠军获得者.
归纳总结
A.抢答:
B.陷阱题:
C.综合题:
当被开方数是多项式时,先要因式分解化为积的形式.
练一练
归纳
1.下列运算正确的是( )
A.
B.
C.
D.
D
当堂练习
2.填空:
2
3. 比较下列两组数的大小(在横线上填“>”“<”或“=”).
>
<
4. 若 成立,则x的取值范围是 .
5.设长方形的面积为S,相邻两边分别为 , .
(1)已知 , ,求S;
解:由题意得:
S = =
= =
=
(2)已知 , ,求S.
解:由题意得:
S = =
= =
=
6.设正方形的面积为S,边长为 .
(1)已知S=50,求 ;
解:由题意得:
= =
= =
=
(2)已知S=242,求 .
解:由题意得:
= =
= =
=
课堂小结
二次根式乘法
法则
性质
拓展法则:
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
16.2 二根次式的乘除
第1课时 二次根式的乘法
第十六章 二次根式
情境引入
1.理解二次根式的乘法法则及积的算术平方根的性质.(重点)
2.合理简洁地进行二次根式的乘法运算.(难点)
学习目标
下面是意大利艺术家列奥纳多·达·芬奇所创作世界名画,请根据不同的已知条件,分别表示出它的面积.
(1)当长为2m,宽为3n,则面积S= ;
(2)当长为 , 宽为 时,则S= ;
6mn
你知道这是什么运算?又如何进行计算呢?
导入新课
二次根式的乘法
1.计算下列各式:
6
6
20
20
30
30
观察计算结果,你发现什么规律?
一
讲授新课
用你发现的规律填空:
当a≥0,b≥0时, 与 大小关系?
=
=
猜一猜
根据积的乘方法则,有
所以
就是ab算术平方根.
而 表示ab算术平方根.
即
证一证
二次根式的乘法法则
首页
文字叙述
算术平方根的乘积等于各个被开方数积的算术平方根.
a,b都必须是非负数.
归纳总结
要点提醒
计算:
解:
例1
纳
典例精析
(1)(2)属于两个二次根式的乘法,按照法则进行计算即可;(3)只需其中两个结合就可实现转化进行计算.(3)说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即 .
归纳
试回顾如何计算3a2·2a3= .
还记得单项式乘以单项式的法则吗?
如何计算呢?
6a5
解:
形如 的乘法
二
想一想
二次根式的乘法扩充法则
第一步:根号外的系数与系数相乘,积为结果的系数;
第二步:根式和根式按公式相乘.
利用它可以进行二次根式的化简.
归纳总结
积的算术平方根的性质及应用
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
在本章中,如果没有特别说明,所有的字母都表示正数.
这个性质在有的地方称之为“积的算术平方根的性质”
三
解:(1) ;
计算:
(1) ;(2) .
(2)
例2
计算:
(1) ;(2) ;(3) .
解:(1)
(2)
(3)
例3
在化简 时,小明是这样进行的:
解:
假如你是他的数学老师,你认为他做对了吗?为什么?如果不对,请改正过来!
答:不对.被开方数的两个因数是负数,不能直接套用积的算术平方根的性质.
正确解法:
议一议
在使用上述积的算术平方根的性质进行计算时,一定要注意前提条件即被开方数的每个因数都必须为非负数.对于不能直接用的,一定要先进行适当转化.
要点提醒
现在你能用上面的性质说明 吗?
抢答游戏:
将从1至100的非平方数的算术平方根的结果快速说出来.竞赛方法:1.四人一组;2.一人报数,一人评判并记录;3.两位同学抢答结果,此为第一轮比赛结果;4.胜者与第三人按同样的方法;5.最后决出本小组的冠军;6.本小组成员用掌声祝贺冠军获得者.
归纳总结
A.抢答:
B.陷阱题:
C.综合题:
当被开方数是多项式时,先要因式分解化为积的形式.
练一练
归纳
1.下列运算正确的是( )
A.
B.
C.
D.
D
当堂练习
2.填空:
2
3. 比较下列两组数的大小(在横线上填“>”“<”或“=”).
>
<
4. 若 成立,则x的取值范围是 .
5.设长方形的面积为S,相邻两边分别为 , .
(1)已知 , ,求S;
解:由题意得:
S = =
= =
=
(2)已知 , ,求S.
解:由题意得:
S = =
= =
=
6.设正方形的面积为S,边长为 .
(1)已知S=50,求 ;
解:由题意得:
= =
= =
=
(2)已知S=242,求 .
解:由题意得:
= =
= =
=
课堂小结
二次根式乘法
法则
性质
拓展法则:
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
