10.1.2轴对称的再认识 课件(共24张PPT)
文档属性
| 名称 | 10.1.2轴对称的再认识 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 14:35:54 | ||
图片预览








文档简介
(共24张PPT)
2022年春华师大版数学
七年级下册数学精品课件
学习目标
探究轴对称现象的共同特点;轴对称图形与垂直平分线的联系.
垂直平分线及角平分线的性质与应用.
对称现象无处不在,那么线段是对称图形么?
A
B
回忆
把一个图形沿某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形.
什么是轴对称图形?
问题1
知识精讲
操作:请同学们完成课本第84页的“做一做”栏目.看看线段OA和OB是否重合?
O为AB中点
显然有线段OA和OB是重合,
所以线段是轴对称图形
D
A
B
O
C
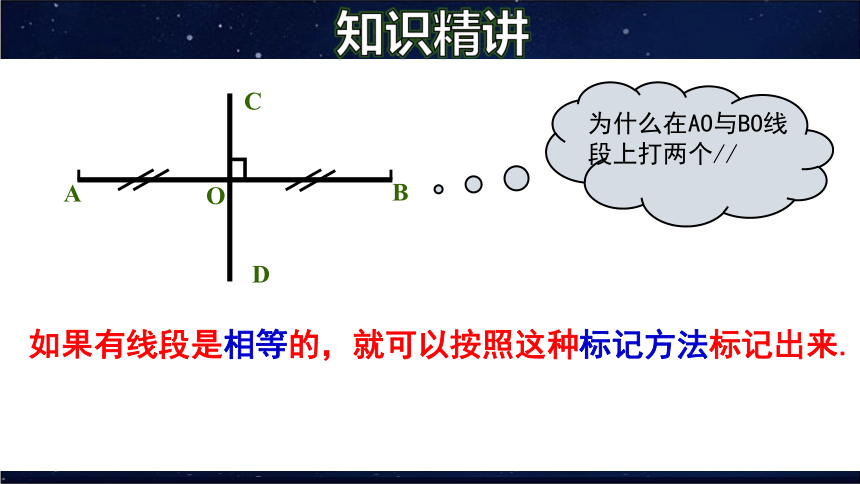
知识精讲
D
A
B
O
C
为什么在AO与BO线段上打两个//
如果有线段是相等的,就可以按照这种标记方法标记出来.
知识精讲
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。
垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线.
总结
知识精讲
O为AB中点
线段MA和MB会重合吗?
A
B
O
C
D
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合。
线段的垂直平分线上的点到这条线段两个端点的距离相等。这是线段垂直平分线的重要性质。
结论:
知识精讲
1.既垂直又平分线段的直线叫做这条线段的垂直平分线.
2.线段的垂直平分线上的点到这条线段两个端点的距离相等.
重点强调
知识精讲
问题2
什么是角?什么是角平分线?角是不是轴对称图形呢?
A
B
O
角是由两条有公共端点的射线组成的几何对象
从一个角的顶点引出一条射线(线在角内),把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线
知识精讲
试验:按以下方法试验,使同学认识角是轴对称图形.
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.
A
B
O
P
结论:角是轴对称图形
知识精讲
如图,请画出它们的对称轴.
针对练习
课本10.1.5,方格子内的两图形都是轴对称图形,我们可以凭借直觉很准确的画出两个图形的对称轴,那没有方格子,又不能折叠时,如何准确的画出图形的对称轴呢?请试着画出下列图形的对称轴.
知识精讲
如图10.1.7,点A和点A'关于某条直线成轴对称,你能画出这条直线么?
做法:
(1)连接点A和点A';
(2)作线段AA'的垂直平分线l.
则直线l为所求图形的对称轴
l
知识精讲
画轴对称图形的对称轴的方法:
先找到轴对称图形的任意一组对称点,连接对称点,得到一条线段,再画出这条线段的垂直平分线,就可以得到该图形的对称轴.
知识精讲
1.画出下列图形的对称轴
做法:
(1)连接
(2)截取;(取中点)
(3)作中垂线.
结论:如果一个图形是轴对称图形,那么连接对称点的线段的垂直平分线是该图形的对称轴.
针对练习
2.如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点.
A
B
解:已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.
作法:①作点A关于CD的对称点A’
②连结A'B交CD于点M
则点M即为所求的点.
A′
河
M
C
D
E
针对练习
M′
3.如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点.
A
B
证明:在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′
∴AM+BM=A′M+BM=A′B
在△A′M′B中
∵A′M′+BM′>A′B(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM
即AM+BM最小.
A′
河
M
C
D
E
针对练习
四、练习
一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
4.成轴对称的两个多边形,一个周长为15cm,则另一个多边形的周长为 cm.
无数
无数
1
2
补充知识:直线也是轴对称图形,有无数条对称轴射线也是轴对称图形,对称轴是自身所在的直线.
15
达标检测
下面的一些虚线,那些是图形的对称轴,那些不是?
达标检测
名称 常见的对称图形 对称轴的条数 对称轴
角 1 角平分线所在的直线
线段 2 线段垂直平分线和线段所在的直线
等腰三角形 1 等腰三角形底边上的高所在的直线
等边三角形 3 等边三角形各边上的高所在的直线
圆 无数条 过圆心的任意一条直线
正方形 4 两条对角线所在的直线以及两组对边中点所在直线
长方形 2 两组对边中点所在的直线
菱形 2 两条对角线所在直线
等腰梯形 1 上下底边中点所在直线
拓展提升
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
学习目标
探究轴对称现象的共同特点;轴对称图形与垂直平分线的联系.
垂直平分线及角平分线的性质与应用.
对称现象无处不在,那么线段是对称图形么?
A
B
回忆
把一个图形沿某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形.
什么是轴对称图形?
问题1
知识精讲
操作:请同学们完成课本第84页的“做一做”栏目.看看线段OA和OB是否重合?
O为AB中点
显然有线段OA和OB是重合,
所以线段是轴对称图形
D
A
B
O
C
知识精讲
D
A
B
O
C
为什么在AO与BO线段上打两个//
如果有线段是相等的,就可以按照这种标记方法标记出来.
知识精讲
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。
垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线.
总结
知识精讲
O为AB中点
线段MA和MB会重合吗?
A
B
O
C
D
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合。
线段的垂直平分线上的点到这条线段两个端点的距离相等。这是线段垂直平分线的重要性质。
结论:
知识精讲
1.既垂直又平分线段的直线叫做这条线段的垂直平分线.
2.线段的垂直平分线上的点到这条线段两个端点的距离相等.
重点强调
知识精讲
问题2
什么是角?什么是角平分线?角是不是轴对称图形呢?
A
B
O
角是由两条有公共端点的射线组成的几何对象
从一个角的顶点引出一条射线(线在角内),把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线
知识精讲
试验:按以下方法试验,使同学认识角是轴对称图形.
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.
A
B
O
P
结论:角是轴对称图形
知识精讲
如图,请画出它们的对称轴.
针对练习
课本10.1.5,方格子内的两图形都是轴对称图形,我们可以凭借直觉很准确的画出两个图形的对称轴,那没有方格子,又不能折叠时,如何准确的画出图形的对称轴呢?请试着画出下列图形的对称轴.
知识精讲
如图10.1.7,点A和点A'关于某条直线成轴对称,你能画出这条直线么?
做法:
(1)连接点A和点A';
(2)作线段AA'的垂直平分线l.
则直线l为所求图形的对称轴
l
知识精讲
画轴对称图形的对称轴的方法:
先找到轴对称图形的任意一组对称点,连接对称点,得到一条线段,再画出这条线段的垂直平分线,就可以得到该图形的对称轴.
知识精讲
1.画出下列图形的对称轴
做法:
(1)连接
(2)截取;(取中点)
(3)作中垂线.
结论:如果一个图形是轴对称图形,那么连接对称点的线段的垂直平分线是该图形的对称轴.
针对练习
2.如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点.
A
B
解:已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.
作法:①作点A关于CD的对称点A’
②连结A'B交CD于点M
则点M即为所求的点.
A′
河
M
C
D
E
针对练习
M′
3.如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点.
A
B
证明:在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′
∴AM+BM=A′M+BM=A′B
在△A′M′B中
∵A′M′+BM′>A′B(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM
即AM+BM最小.
A′
河
M
C
D
E
针对练习
四、练习
一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
4.成轴对称的两个多边形,一个周长为15cm,则另一个多边形的周长为 cm.
无数
无数
1
2
补充知识:直线也是轴对称图形,有无数条对称轴射线也是轴对称图形,对称轴是自身所在的直线.
15
达标检测
下面的一些虚线,那些是图形的对称轴,那些不是?
达标检测
名称 常见的对称图形 对称轴的条数 对称轴
角 1 角平分线所在的直线
线段 2 线段垂直平分线和线段所在的直线
等腰三角形 1 等腰三角形底边上的高所在的直线
等边三角形 3 等边三角形各边上的高所在的直线
圆 无数条 过圆心的任意一条直线
正方形 4 两条对角线所在的直线以及两组对边中点所在直线
长方形 2 两组对边中点所在的直线
菱形 2 两条对角线所在直线
等腰梯形 1 上下底边中点所在直线
拓展提升
https://www.21cnjy.com/help/help_extract.php
