10.2.2平移的特征 课件(共27张PPT)
文档属性
| 名称 | 10.2.2平移的特征 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 08:59:04 | ||
图片预览








文档简介
(共27张PPT)
2022年春华师大版数学
七年级下册数学精品课件
学习目标
能根据所给条件作简单的平面图形平移后的图形;运用平移进行图案设计.
探索平移的特征,准确理解平移的特征和平移的基本性质.
什么是平移?
(1)图形的________,简称为平移。它是图形的又一变换.
(2)平移是由________和________决定的.
平行移动
平移方向
平移距离
复习回顾
A
B
C
A'
B'
C'
观察右图,请回答:
1.平移后的图形与原来的图形的形状、大小有没有发变化?
2.平移后的图形与原来的图形的对应线段、对应角各有什么关系?
没有
平移后的图形与原来的图形的对应线段平行且相等,对应角相等。
注意:
在平移过程中,对应线段也可能在一条直线上,如图中的B’C’ 与BC
这就是平移的特征之一
知识精讲
动手操作,感悟规律
在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A″B″C″.△A″B″C″是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
知识精讲
归纳规律
经过几次平移后得到的图形,可以看成图形经过一次平移得到.也就是说多次平移相当于一次平移.
知识精讲
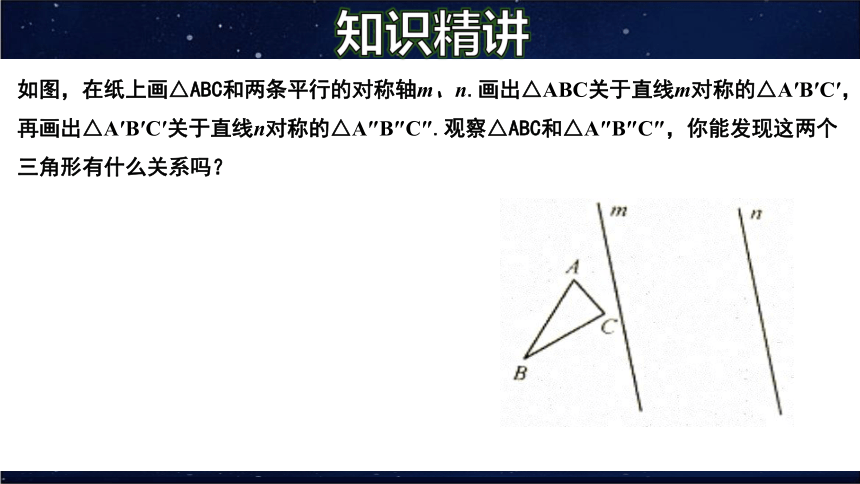
如图,在纸上画△ABC和两条平行的对称轴m、n.画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
知识精讲
经过两次翻折(对称轴互相平行)后所得到的图形,可以看成是原图形经过平移得到.
也就是说两次翻折相当于一次平移.
知识精讲
总结规律
知识精讲
观察与思考
△ABC经过平移得到△A’B’C’
平行 (在同一直线上)且相等
1.连接几组对应点(如:A与A‘,B与B’,C与C‘)观察得到的线段,它们的位置、长短有什么关系?对应线段呢?对应角呢?
对应角相等
经过平移:
1.新图形与原图形的形状、大小及方向完全相同;
2.对应点所连的线段平行(或在一条直线上)且相等;
3.对应线段平行(或在一条直线上)且相等;
4.对应角相等.
2
知识点
平移的性质
知识精讲
要点精析:
(1)连接对应点的线段的长度就是平移的距离;
(2)从原图上一点到其对应点的方向,即起始点到终止
点的方向为平移的方向.
知识精讲
例1 如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
典例解析
B
C
A
例2:如图,经过平移,三角形ABC的顶点A移到了点D,作出平移后的三角形.
E
F
D
解:如图,连接AD,过B、C点分别做线段BE、CF使得他们与线段AD平行且相等,连接 DE、DF、EF,三角形DEF就是三角形ABC平移后的图形.
典例解析
思考:有其他的方法吗?
解:如图,过点D按射线AB的方向做线段DE平行且等于线段AB;过点D按射线AC的方向做线段DF平行且等于线段AC;连接EF. 三角形DEF就是ΔABC平移后的图形.
典例解析
B
C
A
E
F
D
如图,将字母A按箭头所指的方向平移3cm,做出平移后的图形.
3cm
平移作图的步骤:
1)找关键点(一般是图形的顶点);
2)根据平移的距离和方向作出这些点经过平移后的对应点;
3)将所作对应点按原来已知图形的连接方式连接起来,所得图形即为所求.
针对练习
1m
1m
21m
15m
A
C
D
B
图 1
例3:如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
思路点拨:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
典例解析
1m
21m
15m
A
C
D
B
如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
针对练习
1.若∠A=60o,将∠A先向左平移1cm,再向下平移2cm,则∠A的大小( )
A、变小 B、变大 C、不变 D、无法确定
2.将线段AB=2cm,向右平移3cm后得到线段CD,则线段CD= cm,BD= cm.
A
B
D
C
C
2
3
达标检测
A
A'
3.将下图形如何移动可移至A'处?说一说
达标检测
P
Q
R
S
B
C
A
A’
B’
C’
A”
B”
C”
4.将图中的 △A'B'C'沿RS方向平移到△A''B''C''的位置,其平移的距离是线段RS的长度.
△
达标检测
5.如图:ΔDEF可以看作ΔABC平移得到
1)平移的方向是 ;平移的距离是 .
2)AB∥ ; ∥ .
3)若BC=5cm,CF=3cm,
则BE= cm,CE= cm,EF= cm.
4)若连结AD,与AD相等的线段是: .
DE
AC
DF
3
2
5
BE
CF
达标检测
6. 已知梯形ABCD中,AD∥BC,AB=DC=3cm,AD=2cm,∠C=60o ,求线段BC的长.
E
提示:利用平行四边形的对边相等,正三角形的三条边均相等可以得出BC的长为5cm
达标检测
7.如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
提示:根据平移的特征可以得到DF//AC,则得到∠DGB=∠C=35°∠E=∠B=105°
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
学习目标
能根据所给条件作简单的平面图形平移后的图形;运用平移进行图案设计.
探索平移的特征,准确理解平移的特征和平移的基本性质.
什么是平移?
(1)图形的________,简称为平移。它是图形的又一变换.
(2)平移是由________和________决定的.
平行移动
平移方向
平移距离
复习回顾
A
B
C
A'
B'
C'
观察右图,请回答:
1.平移后的图形与原来的图形的形状、大小有没有发变化?
2.平移后的图形与原来的图形的对应线段、对应角各有什么关系?
没有
平移后的图形与原来的图形的对应线段平行且相等,对应角相等。
注意:
在平移过程中,对应线段也可能在一条直线上,如图中的B’C’ 与BC
这就是平移的特征之一
知识精讲
动手操作,感悟规律
在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A″B″C″.△A″B″C″是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
知识精讲
归纳规律
经过几次平移后得到的图形,可以看成图形经过一次平移得到.也就是说多次平移相当于一次平移.
知识精讲
如图,在纸上画△ABC和两条平行的对称轴m、n.画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
知识精讲
经过两次翻折(对称轴互相平行)后所得到的图形,可以看成是原图形经过平移得到.
也就是说两次翻折相当于一次平移.
知识精讲
总结规律
知识精讲
观察与思考
△ABC经过平移得到△A’B’C’
平行 (在同一直线上)且相等
1.连接几组对应点(如:A与A‘,B与B’,C与C‘)观察得到的线段,它们的位置、长短有什么关系?对应线段呢?对应角呢?
对应角相等
经过平移:
1.新图形与原图形的形状、大小及方向完全相同;
2.对应点所连的线段平行(或在一条直线上)且相等;
3.对应线段平行(或在一条直线上)且相等;
4.对应角相等.
2
知识点
平移的性质
知识精讲
要点精析:
(1)连接对应点的线段的长度就是平移的距离;
(2)从原图上一点到其对应点的方向,即起始点到终止
点的方向为平移的方向.
知识精讲
例1 如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
典例解析
B
C
A
例2:如图,经过平移,三角形ABC的顶点A移到了点D,作出平移后的三角形.
E
F
D
解:如图,连接AD,过B、C点分别做线段BE、CF使得他们与线段AD平行且相等,连接 DE、DF、EF,三角形DEF就是三角形ABC平移后的图形.
典例解析
思考:有其他的方法吗?
解:如图,过点D按射线AB的方向做线段DE平行且等于线段AB;过点D按射线AC的方向做线段DF平行且等于线段AC;连接EF. 三角形DEF就是ΔABC平移后的图形.
典例解析
B
C
A
E
F
D
如图,将字母A按箭头所指的方向平移3cm,做出平移后的图形.
3cm
平移作图的步骤:
1)找关键点(一般是图形的顶点);
2)根据平移的距离和方向作出这些点经过平移后的对应点;
3)将所作对应点按原来已知图形的连接方式连接起来,所得图形即为所求.
针对练习
1m
1m
21m
15m
A
C
D
B
图 1
例3:如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
思路点拨:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
典例解析
1m
21m
15m
A
C
D
B
如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
针对练习
1.若∠A=60o,将∠A先向左平移1cm,再向下平移2cm,则∠A的大小( )
A、变小 B、变大 C、不变 D、无法确定
2.将线段AB=2cm,向右平移3cm后得到线段CD,则线段CD= cm,BD= cm.
A
B
D
C
C
2
3
达标检测
A
A'
3.将下图形如何移动可移至A'处?说一说
达标检测
P
Q
R
S
B
C
A
A’
B’
C’
A”
B”
C”
4.将图中的 △A'B'C'沿RS方向平移到△A''B''C''的位置,其平移的距离是线段RS的长度.
△
达标检测
5.如图:ΔDEF可以看作ΔABC平移得到
1)平移的方向是 ;平移的距离是 .
2)AB∥ ; ∥ .
3)若BC=5cm,CF=3cm,
则BE= cm,CE= cm,EF= cm.
4)若连结AD,与AD相等的线段是: .
DE
AC
DF
3
2
5
BE
CF
达标检测
6. 已知梯形ABCD中,AD∥BC,AB=DC=3cm,AD=2cm,∠C=60o ,求线段BC的长.
E
提示:利用平行四边形的对边相等,正三角形的三条边均相等可以得出BC的长为5cm
达标检测
7.如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
提示:根据平移的特征可以得到DF//AC,则得到∠DGB=∠C=35°∠E=∠B=105°
达标检测
https://www.21cnjy.com/help/help_extract.php
