10.4中心对称 课件(共25张PPT)
文档属性
| 名称 | 10.4中心对称 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 08:40:11 | ||
图片预览







文档简介
(共25张PPT)
2022年春华师大版数学
七年级下册数学精品课件
中心对称
学习目标
知道中心对称与中心对称图形的意义.
知道成中心对称的两个图形的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
这些图形都可以绕哪个点旋转多少度后与原来的图形重合
知识精讲
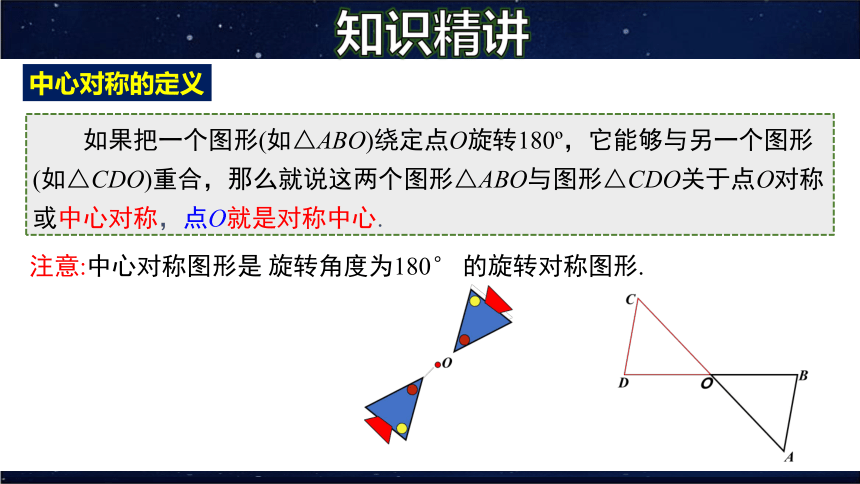
如果把一个图形(如△ABO)绕定点O旋转180 ,它能够与另一个图形(如△CDO)重合,那么就说这两个图形△ABO与图形△CDO关于点O对称或中心对称,点O就是对称中心.
中心对称的定义
知识精讲
注意:中心对称图形是 旋转角度为180° 的旋转对称图形.
中心对称和中心对称图形的区别:
中心对称是指两个图形,而中心对称图形是指一个图形.
知识精讲
观察
A’
A
B’
B
C’
C
O
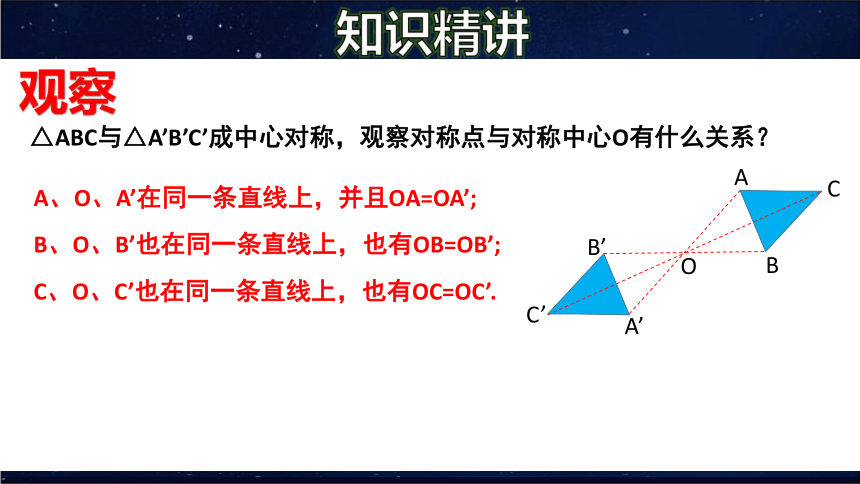
△ABC与△A’B’C’成中心对称,观察对称点与对称中心O有什么关系?
A、O、A’在同一条直线上,并且OA=OA’;
B、O、B’也在同一条直线上,也有OB=OB’;
C、O、C’也在同一条直线上,也有OC=OC’.
知识精讲
中心对称的性质:
性质1:在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
性质2:如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
知识精讲
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
对比分析
例1
如图,已知△ABC和点O,请画出△ABC关于点O成中心对称的△DEF,
A
B
C
O
解
1.作点A关于点O的对称点D;
D
2.作点B关于点O的对称点E;
E
3.作点C关于点O的对称点F;
F
4.顺次连结DE、EF、FD.
则△DEF为所求作的三角形.
典例解析
归纳
成中心对称的图形的画法:
1.分别作图形关键点关于对称中心的对称点;
2.顺次连结各对称点得到一个图形;
3.下结论:所得到的图形为所求作的图形.
总结提升
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
典例解析
例1
(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
典例解析
解
名称 中心对称 中心对称图形
定义
联系 把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形成对称中心,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
知识精讲
1.中心对称图形的概念:
把_____个图形绕着中心旋转_____后能与_______重合,我们把这种图形叫做中心对称图形,这个中心叫做___________.
一
1800
自身
对称中心
2.下列汽车标志图形哪些是中心对称图形:_______________.
①
②
③
④
⑤
②、③、⑤
达标检测
3.下列图形中,是中心对称图形的是( )
A
达标检测
4.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
A
达标检测
5.按下列要求正确画出图形:
(1)已知△ABC和直线MN,画出△ABC关于直线MN对称的图形;
(2)已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
达标检测
解:(1)过点A作AA′⊥MN且使MN垂直平分AA′,过点B作BB′⊥MN且使MN垂直平分BB′,过点C作CC′⊥MN且使MN垂直平分CC′,然后顺次连接即可;
△A′B′C′如图所示;
达标检测
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
达标检测
6.如图,在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 求对称中心E点的坐标.
分析:连接对应点AA1、CC1,根据对应点的连线经过对称中心,则交点就是对称中心E点,在坐标系内确定出其坐标.
达标检测
解:连接AA1、CC1,则交点就是对称中心E点.观察图形知E(3,-1)
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
中心对称
学习目标
知道中心对称与中心对称图形的意义.
知道成中心对称的两个图形的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
这些图形都可以绕哪个点旋转多少度后与原来的图形重合
知识精讲
如果把一个图形(如△ABO)绕定点O旋转180 ,它能够与另一个图形(如△CDO)重合,那么就说这两个图形△ABO与图形△CDO关于点O对称或中心对称,点O就是对称中心.
中心对称的定义
知识精讲
注意:中心对称图形是 旋转角度为180° 的旋转对称图形.
中心对称和中心对称图形的区别:
中心对称是指两个图形,而中心对称图形是指一个图形.
知识精讲
观察
A’
A
B’
B
C’
C
O
△ABC与△A’B’C’成中心对称,观察对称点与对称中心O有什么关系?
A、O、A’在同一条直线上,并且OA=OA’;
B、O、B’也在同一条直线上,也有OB=OB’;
C、O、C’也在同一条直线上,也有OC=OC’.
知识精讲
中心对称的性质:
性质1:在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
性质2:如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
知识精讲
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
对比分析
例1
如图,已知△ABC和点O,请画出△ABC关于点O成中心对称的△DEF,
A
B
C
O
解
1.作点A关于点O的对称点D;
D
2.作点B关于点O的对称点E;
E
3.作点C关于点O的对称点F;
F
4.顺次连结DE、EF、FD.
则△DEF为所求作的三角形.
典例解析
归纳
成中心对称的图形的画法:
1.分别作图形关键点关于对称中心的对称点;
2.顺次连结各对称点得到一个图形;
3.下结论:所得到的图形为所求作的图形.
总结提升
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
典例解析
例1
(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
典例解析
解
名称 中心对称 中心对称图形
定义
联系 把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形成对称中心,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
知识精讲
1.中心对称图形的概念:
把_____个图形绕着中心旋转_____后能与_______重合,我们把这种图形叫做中心对称图形,这个中心叫做___________.
一
1800
自身
对称中心
2.下列汽车标志图形哪些是中心对称图形:_______________.
①
②
③
④
⑤
②、③、⑤
达标检测
3.下列图形中,是中心对称图形的是( )
A
达标检测
4.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
A
达标检测
5.按下列要求正确画出图形:
(1)已知△ABC和直线MN,画出△ABC关于直线MN对称的图形;
(2)已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
达标检测
解:(1)过点A作AA′⊥MN且使MN垂直平分AA′,过点B作BB′⊥MN且使MN垂直平分BB′,过点C作CC′⊥MN且使MN垂直平分CC′,然后顺次连接即可;
△A′B′C′如图所示;
达标检测
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
达标检测
6.如图,在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 求对称中心E点的坐标.
分析:连接对应点AA1、CC1,根据对应点的连线经过对称中心,则交点就是对称中心E点,在坐标系内确定出其坐标.
达标检测
解:连接AA1、CC1,则交点就是对称中心E点.观察图形知E(3,-1)
达标检测
https://www.21cnjy.com/help/help_extract.php
