10.5图形的全等 课件(共29张PPT)
文档属性
| 名称 | 10.5图形的全等 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
2022年春华师大版数学
七年级下册数学精品课件
学习目标
知道全等图形,全等多边形,全等三角形的概念和性质.
能找出全等多边形、全等三角形的对应元素,会利用图形的全等解决一些简单问题
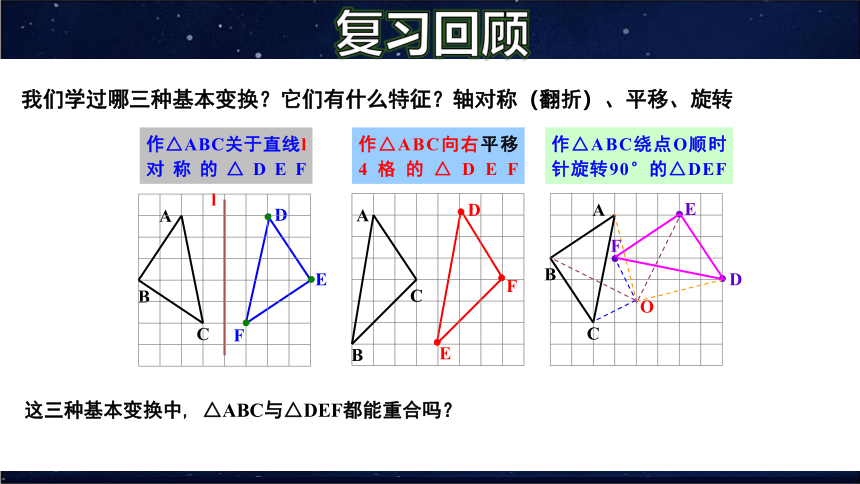
我们学过哪三种基本变换?它们有什么特征?轴对称(翻折)、平移、旋转
D
l
A
B
C
E
F
A
B
C
D
F
E
·
O
A
B
C
D
E
F
这三种基本变换中, △ABC与△DEF都能重合吗?
作△ABC关于直线l对称的△DEF
作△ABC向右平移
4格的△DEF
作△ABC绕点O顺时针旋转90°的△DEF
复习回顾
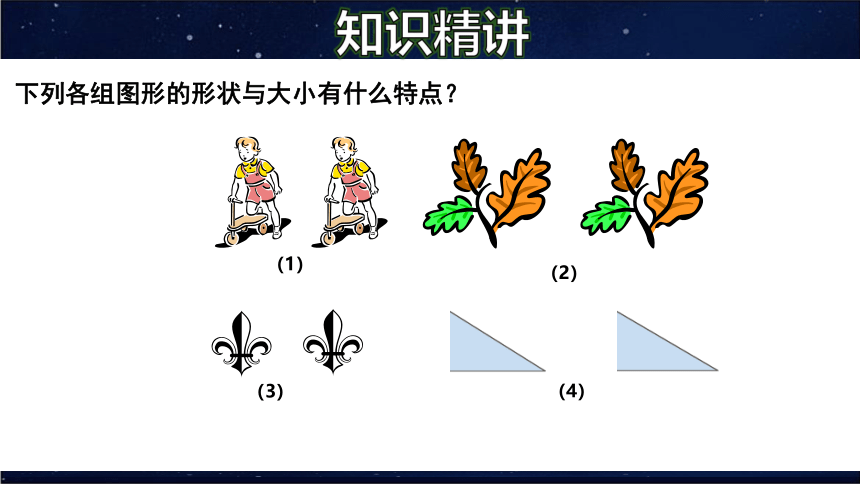
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
知识精讲
观察下面的图形:
从这组图中你看出了什么?
每组图形中的每个图形的形状、大小都一样.
知识精讲
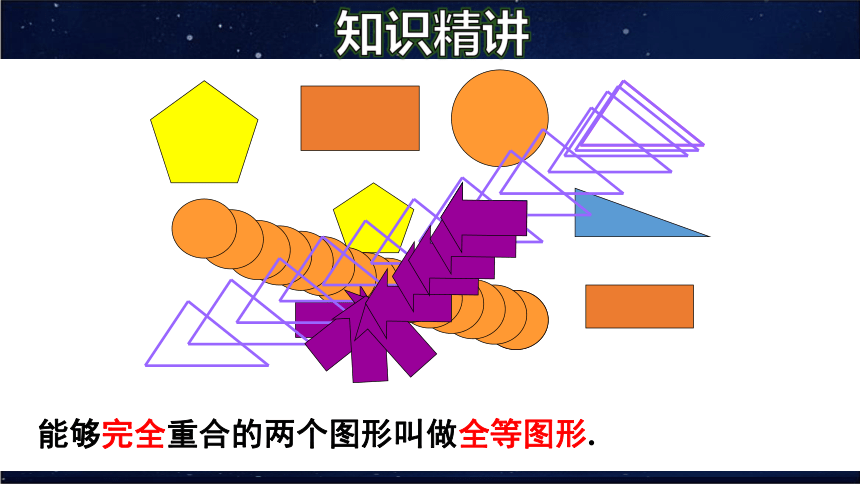
能够完全重合的两个图形叫做全等图形.
知识精讲
图形的全等
我们已经认识了图形的翻折、平移和旋转,这三种
图形基本变换,图形在变换经过中, 发生了改变,
但变换前后的图形对应线段 ,对应角 ,它们
的 并没有改变.
位置
相等
相等
形状和大小
新知讲解
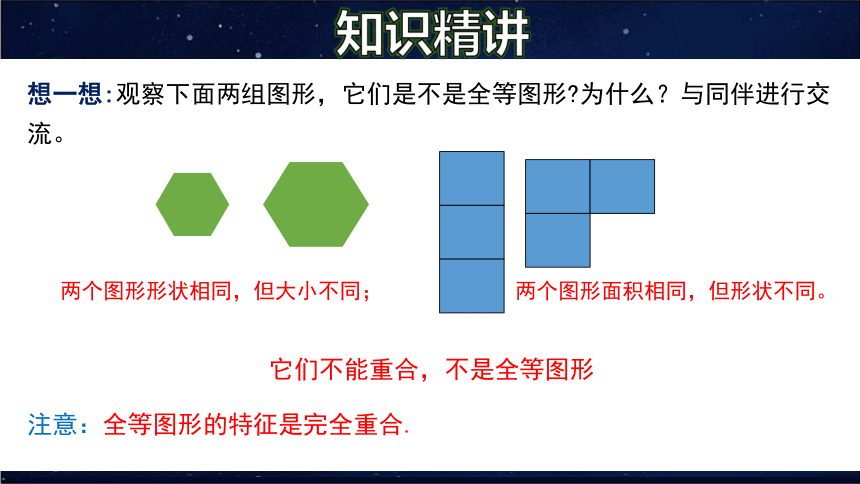
想一想:观察下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同。
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
知识精讲
13和15是由___变换得到的全等图形;
1和9是由___变换得到的全等图形;
7和12是由___变换得到的全等图形;
14和16是由___变换得到的全等图形。
请你说一说,那些是全等图形
针对练习
全等多边形
A
B
C
D
E
A′
B′
C′
D′
E′
能够完全重合的多边形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
全等的数学符号表示为:“≌” ,读作“全等于”
如图中的两个五边形是全等的,记作:
五边形ABCDE ≌ 五边形A′B′C′D′E′
全等多边形有哪些性质呢?
知识精讲
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试 找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D = ∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等图形的性质
≌
新知讲解
针对练习
D
E
F
A
B
C
能够完全重合的两个三角形叫做全等三角形.
知识精讲
D
E
F
A
B
C
如上图:△ABC 与△DEF全等
记作:△ABC≌△DEF
通常把对应的顶点字母写在对应位置上.
全等三角形
“全等”符号:“≌”
读作:△ABC全等于△DEF
表示方法:
注:符号“≌”表示全等,读作“全等于”
知识精讲
A
C
B
F
E
D
想一想
能否记作 ABC≌ DEF
应该记作: ABC≌ DFE
原因:A与D、B与F、C与E对应.
对应顶点要写在对应位置上.
知识精讲
N
M
S
O
T
D
C
O
A
B
仔细观察,再用全等符号表示下列两组全等三角形.
△AOB ≌△DOC
△OAB ≌△ODC
△MON ≌△SOT
针对练习
A
B
C
全等三角形的对应边相等,对应角相等。
∵△ABC≌△DEF
∴AB=DE、BC=EF、CA=FD
∠A=∠D、 ∠B=∠E、 ∠C=∠F
D
E
F
全等三角形性质:
知识精讲
(1)如果△ABC ≌△DEF,那么你可以得到:
(2)如果具备:
∠A=∠D,∠B=∠E,∠C=∠F。
A
B
C
D
E
F
AB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F。
那么可以得出 △ABC ≌△DEF 。
想一想
如图,
AB=DE,BC=EF,AC=DF;
知识精讲
请你找出图中全等三角形的对应边:
A
B
C
D
A
B
C
D
E
F
规律
(1)有公共边的,公共边是对应边;
(2)一对最长的边是对应边,一对最短的边是对应边.
知识精讲
请你找出图中全等三角形的对应角:
C
D
A
B
E
B
D
A
C
O
规律
(1)有公共角的,公共角是对应角;
(2)有对顶角的,对顶角是对应角;
(3)最大角与最大角,最小角与最小角是对应角.
寻找对应边、对应角的方法:
(1)在表达式上找:利用字母的对应位置来确定对应边和对应角。
(2)在图上找:特殊的边和特殊的角。
(3)对应边所对的角是对应角,对应角所对的边是对应边.
知识精讲
A
B
C
D
E
F
例1 如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°∠B=60°,求∠F的度数.
解一:
∵ ABC沿着BC的方向平移至 △DEF
∴ △ABC ≌△DEF
∴ ∠D=∠A,∠DEF= ∠B
∵ ∠A=80 °, ∠B=60 °
∴ ∠D=80 °, ∠DEF=60 °
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °-∠D-∠DEF =40°
典例解析
A
B
C
D
E
F
解二:
∵ ABC沿着BC的方向平移至 △DEF
∴ △ABC ≌△DEF
∴ ∠F=∠ACB
又∵ ∠A+∠B+∠ ACB =180°
∠A=80°, ∠B=60°
∴ ∠ACB=180 °-∠A-∠ ACB=40°
∴ ∠F= 40°
知识精讲
例1 如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°∠B=60°,求∠F的度数.
1.已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知) ∴AC=DF.(全等三角形的对应边等)
∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知)
∴ AC=40-AB-BC=14(cm),
∴ DF=14cm.
A
B
C
D
E
F
针对练习
2.如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
(2)△ABD 满足什么条件时,BD//CE?
B
C
D
A
E
针对练习
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
小结梳理
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
学习目标
知道全等图形,全等多边形,全等三角形的概念和性质.
能找出全等多边形、全等三角形的对应元素,会利用图形的全等解决一些简单问题
我们学过哪三种基本变换?它们有什么特征?轴对称(翻折)、平移、旋转
D
l
A
B
C
E
F
A
B
C
D
F
E
·
O
A
B
C
D
E
F
这三种基本变换中, △ABC与△DEF都能重合吗?
作△ABC关于直线l对称的△DEF
作△ABC向右平移
4格的△DEF
作△ABC绕点O顺时针旋转90°的△DEF
复习回顾
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
知识精讲
观察下面的图形:
从这组图中你看出了什么?
每组图形中的每个图形的形状、大小都一样.
知识精讲
能够完全重合的两个图形叫做全等图形.
知识精讲
图形的全等
我们已经认识了图形的翻折、平移和旋转,这三种
图形基本变换,图形在变换经过中, 发生了改变,
但变换前后的图形对应线段 ,对应角 ,它们
的 并没有改变.
位置
相等
相等
形状和大小
新知讲解
想一想:观察下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同。
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
知识精讲
13和15是由___变换得到的全等图形;
1和9是由___变换得到的全等图形;
7和12是由___变换得到的全等图形;
14和16是由___变换得到的全等图形。
请你说一说,那些是全等图形
针对练习
全等多边形
A
B
C
D
E
A′
B′
C′
D′
E′
能够完全重合的多边形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
全等的数学符号表示为:“≌” ,读作“全等于”
如图中的两个五边形是全等的,记作:
五边形ABCDE ≌ 五边形A′B′C′D′E′
全等多边形有哪些性质呢?
知识精讲
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试 找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D = ∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等图形的性质
≌
新知讲解
针对练习
D
E
F
A
B
C
能够完全重合的两个三角形叫做全等三角形.
知识精讲
D
E
F
A
B
C
如上图:△ABC 与△DEF全等
记作:△ABC≌△DEF
通常把对应的顶点字母写在对应位置上.
全等三角形
“全等”符号:“≌”
读作:△ABC全等于△DEF
表示方法:
注:符号“≌”表示全等,读作“全等于”
知识精讲
A
C
B
F
E
D
想一想
能否记作 ABC≌ DEF
应该记作: ABC≌ DFE
原因:A与D、B与F、C与E对应.
对应顶点要写在对应位置上.
知识精讲
N
M
S
O
T
D
C
O
A
B
仔细观察,再用全等符号表示下列两组全等三角形.
△AOB ≌△DOC
△OAB ≌△ODC
△MON ≌△SOT
针对练习
A
B
C
全等三角形的对应边相等,对应角相等。
∵△ABC≌△DEF
∴AB=DE、BC=EF、CA=FD
∠A=∠D、 ∠B=∠E、 ∠C=∠F
D
E
F
全等三角形性质:
知识精讲
(1)如果△ABC ≌△DEF,那么你可以得到:
(2)如果具备:
∠A=∠D,∠B=∠E,∠C=∠F。
A
B
C
D
E
F
AB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F。
那么可以得出 △ABC ≌△DEF 。
想一想
如图,
AB=DE,BC=EF,AC=DF;
知识精讲
请你找出图中全等三角形的对应边:
A
B
C
D
A
B
C
D
E
F
规律
(1)有公共边的,公共边是对应边;
(2)一对最长的边是对应边,一对最短的边是对应边.
知识精讲
请你找出图中全等三角形的对应角:
C
D
A
B
E
B
D
A
C
O
规律
(1)有公共角的,公共角是对应角;
(2)有对顶角的,对顶角是对应角;
(3)最大角与最大角,最小角与最小角是对应角.
寻找对应边、对应角的方法:
(1)在表达式上找:利用字母的对应位置来确定对应边和对应角。
(2)在图上找:特殊的边和特殊的角。
(3)对应边所对的角是对应角,对应角所对的边是对应边.
知识精讲
A
B
C
D
E
F
例1 如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°∠B=60°,求∠F的度数.
解一:
∵ ABC沿着BC的方向平移至 △DEF
∴ △ABC ≌△DEF
∴ ∠D=∠A,∠DEF= ∠B
∵ ∠A=80 °, ∠B=60 °
∴ ∠D=80 °, ∠DEF=60 °
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °-∠D-∠DEF =40°
典例解析
A
B
C
D
E
F
解二:
∵ ABC沿着BC的方向平移至 △DEF
∴ △ABC ≌△DEF
∴ ∠F=∠ACB
又∵ ∠A+∠B+∠ ACB =180°
∠A=80°, ∠B=60°
∴ ∠ACB=180 °-∠A-∠ ACB=40°
∴ ∠F= 40°
知识精讲
例1 如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°∠B=60°,求∠F的度数.
1.已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知) ∴AC=DF.(全等三角形的对应边等)
∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知)
∴ AC=40-AB-BC=14(cm),
∴ DF=14cm.
A
B
C
D
E
F
针对练习
2.如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
(2)△ABD 满足什么条件时,BD//CE?
B
C
D
A
E
针对练习
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
小结梳理
https://www.21cnjy.com/help/help_extract.php
