2.3.1 平行线的性质 课件(共18张PPT)
文档属性
| 名称 | 2.3.1 平行线的性质 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 19:51:44 | ||
图片预览




文档简介
(共18张PPT)
2.3 平行线的性质
北师版七(下)
第一课时
两直线平行
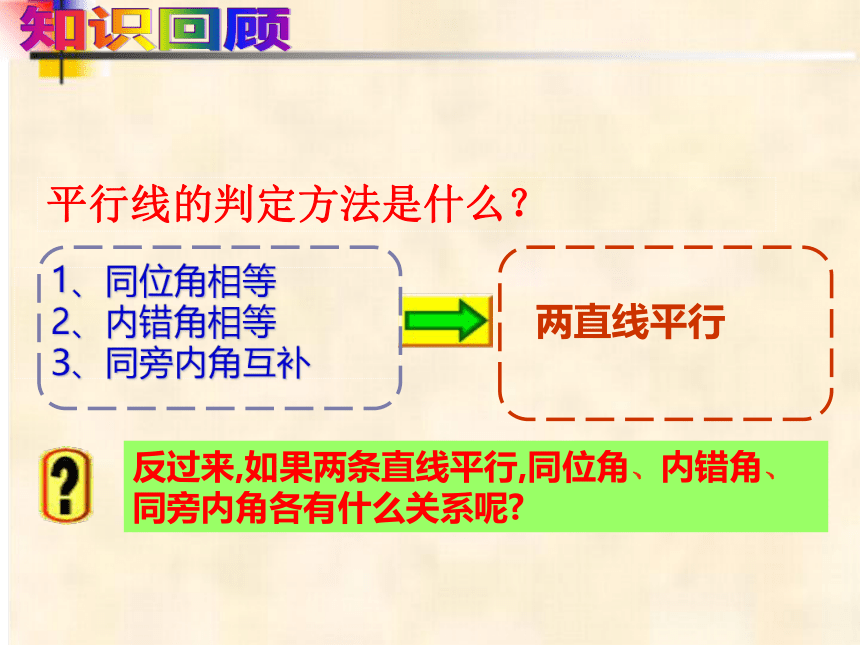
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
知识回顾
c
a
b
1
5
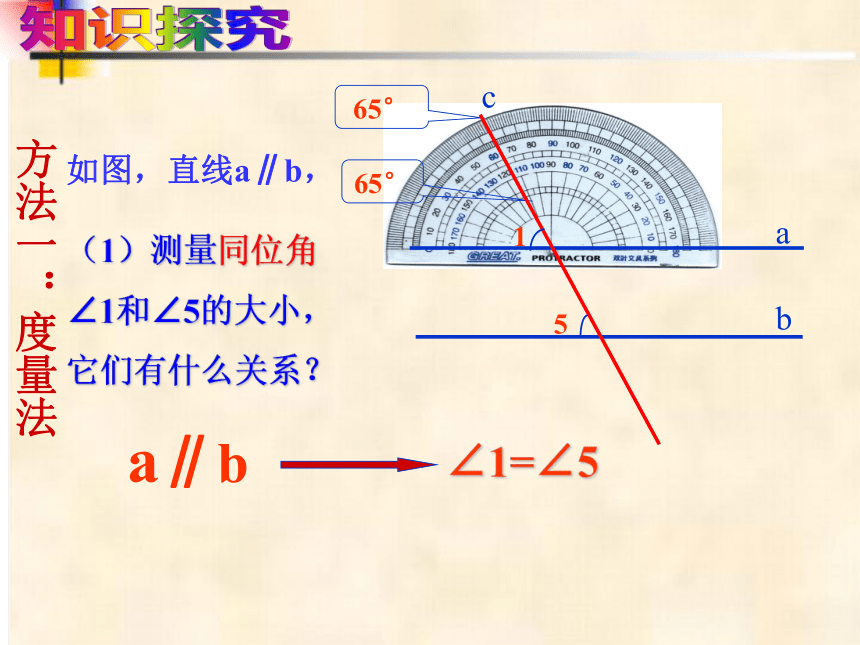
探究:两直线平行,同位角有什么关系
知识探究
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
∠1=∠5
a∥b
方法一:度量法
知识探究
b
5
a
c
1
∠1=∠5
a∥b
方法二:裁剪叠合法
知识探究
c
a
b
问题:如果直线a与b不平行,你的猜想还成立吗?
结论:“同位角相等”不一定正确.
知识探究
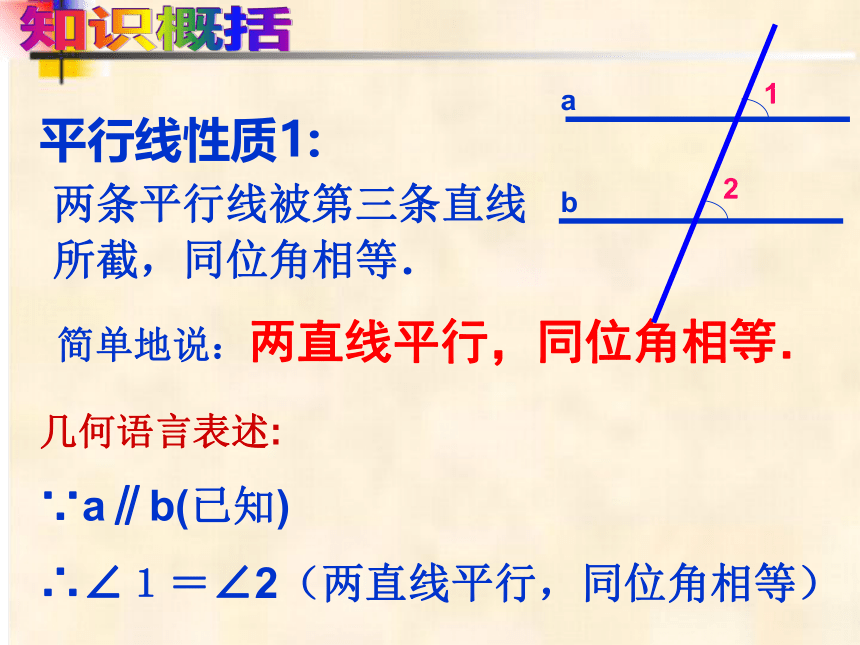
简单地说:两直线平行,同位角相等.
a
b
1
2
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
知识概括
如图,已知:a// b, 那么 3与 2有什么关系?
我们能否依据“两直线平行,同位角相等”来推理内错角和同旁内角的关系呢?
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等 )
又∵∠1=∠3(对顶角相等)
1
2
3
a
b
∴∠2=∠3(等量代换)
知识探究
简单地说:两直线平行,内错角相等.
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
两条平行线被第三条直线所截,内错角相等.
平行线性质2:
1
2
3
a
b
知识概括
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180°(邻补角定义),
∴ 2+ 4=180°(等量代换).
知识探究
简单地说:两直线平行,同旁内角互补.
几何语言表述:
∵a∥b(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
两条平行线被第三条直线所截,同旁内角互补.
平行线性质3:
b
1
2
a
c
4
知识概括
例、已知,AB∥CD, ∠1=45°, ∠D= ∠C,求∠D, ∠C, ∠B的度数。
A
C
B
1
D
典例导学
C
夯实基础
A
C
夯实基础
B
C
夯实基础
4.
5.
夯实基础
6.如图,FE∥AC,,AC平分∠BAF, 如∠B= 800,求∠C的度数。
夯实基础
7.如图,点E、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=45°, 试说明∠1= ∠2的理由。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课内反思
2.3 平行线的性质
北师版七(下)
第一课时
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
知识回顾
c
a
b
1
5
探究:两直线平行,同位角有什么关系
知识探究
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
∠1=∠5
a∥b
方法一:度量法
知识探究
b
5
a
c
1
∠1=∠5
a∥b
方法二:裁剪叠合法
知识探究
c
a
b
问题:如果直线a与b不平行,你的猜想还成立吗?
结论:“同位角相等”不一定正确.
知识探究
简单地说:两直线平行,同位角相等.
a
b
1
2
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
知识概括
如图,已知:a// b, 那么 3与 2有什么关系?
我们能否依据“两直线平行,同位角相等”来推理内错角和同旁内角的关系呢?
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等 )
又∵∠1=∠3(对顶角相等)
1
2
3
a
b
∴∠2=∠3(等量代换)
知识探究
简单地说:两直线平行,内错角相等.
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
两条平行线被第三条直线所截,内错角相等.
平行线性质2:
1
2
3
a
b
知识概括
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180°(邻补角定义),
∴ 2+ 4=180°(等量代换).
知识探究
简单地说:两直线平行,同旁内角互补.
几何语言表述:
∵a∥b(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
两条平行线被第三条直线所截,同旁内角互补.
平行线性质3:
b
1
2
a
c
4
知识概括
例、已知,AB∥CD, ∠1=45°, ∠D= ∠C,求∠D, ∠C, ∠B的度数。
A
C
B
1
D
典例导学
C
夯实基础
A
C
夯实基础
B
C
夯实基础
4.
5.
夯实基础
6.如图,FE∥AC,,AC平分∠BAF, 如∠B= 800,求∠C的度数。
夯实基础
7.如图,点E、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=45°, 试说明∠1= ∠2的理由。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课内反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
