2.3.2平行线的性质(第二课时) 课件(共10张PPT)
文档属性
| 名称 | 2.3.2平行线的性质(第二课时) 课件(共10张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 08:24:44 | ||
图片预览


文档简介
(共10张PPT)
2.3 平行线的性质
北师版七(下)
第二课时
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
知识回顾
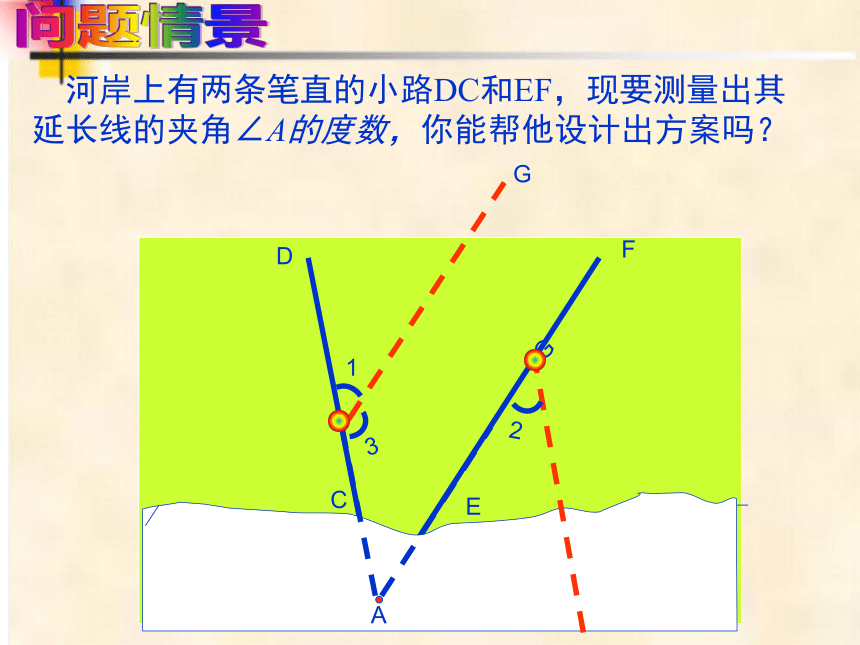
河岸上有两条笔直的小路DC和EF,现要测量出其延长线的夹角∠A的度数,你能帮他设计出方案吗?
D
C
E
F
A
A
G
G
1
2
问题情景
3
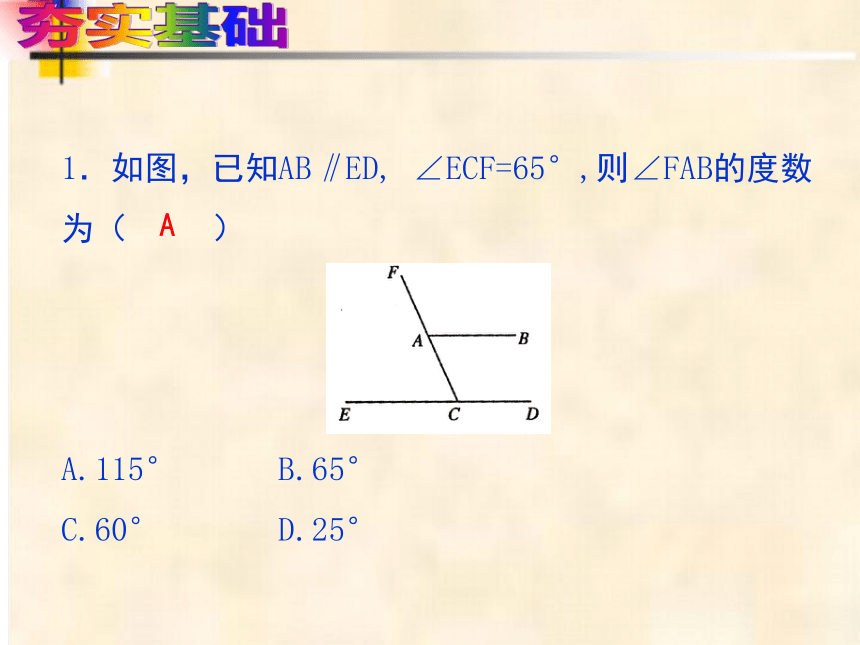
1.如图,已知AB‖ED, ∠ECF=65°,则∠FAB的度数为( )
A.115° B.65°
C.60° D.25°
A
夯实基础
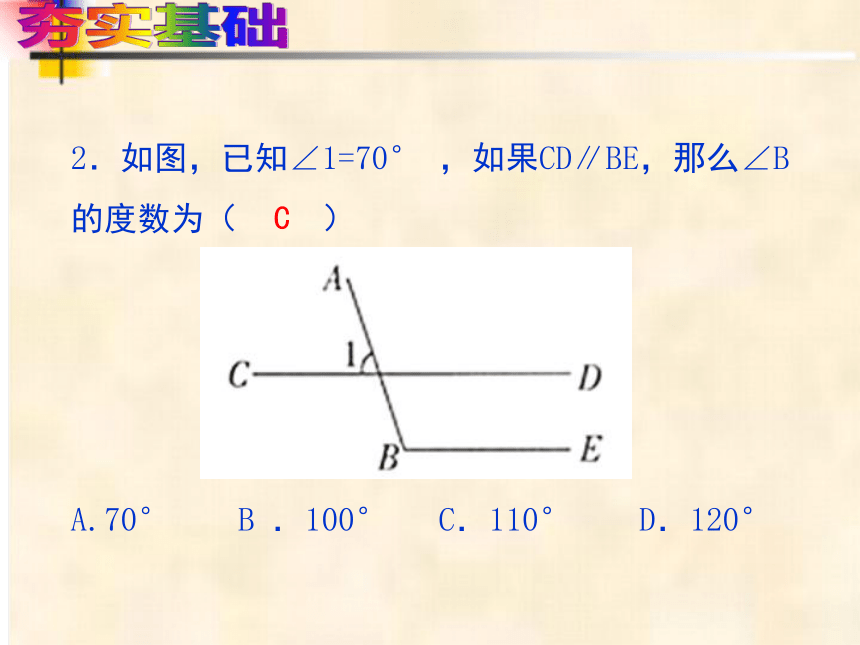
2.如图,已知∠1=70° ,如果CD∥BE,那么∠B的度数为( )
A.70° B .100° C.110° D.120°
C
夯实基础
3. 下列图形中,由AB‖CD ,能得到∠1=∠2的是( )
B
夯实基础
4.如图,已知AG‖CF,AB‖CD,∠A=40°,求∠C的度数.
F
A
B
C
D
E
G
解 ∵AG∥CF( )
∴∠A=∠BEF( )
∵AB∥CD( )
∴∠C=∠BEF( )
∴∠A=∠C=400( )
已知
两直线平行,同位角相等
已知
两直线平行,同位角相等
等量代换
夯实基础
5、如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=50°,求∠EFC的度数
解 ∵∠1=500( )
∠1+∠DED'=1800( )
∴∠DED'=1300
∴∠D'EF=∠DEF=650
∵AD∥CBD( )
∴∠DEF+∠EFC=1800( )
∴∠EFC=1800-650=1150
已知
平角的定义
已知
两直线平行,内错角互补
夯实基础
如图,若AB//CD,求∠B、
∠D与∠BED的关系。
解:
过点E作EF//AB.
∴∠B=∠BEF ( )
∵AB∥CD( )
AB∥EF( )
∴EF∥CD( )
∴∠D=∠DEF( )
∴∠B+∠D=∠BEF+∠DEF=∠BED( )
两直线平行,内错角相等
已知
辅助线
平行于同一直线的两条直线也平行
两直线平行,内错角相等
等式的性质
A
B
C
D
E
F
能力提升
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课内反思
2.3 平行线的性质
北师版七(下)
第二课时
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
知识回顾
河岸上有两条笔直的小路DC和EF,现要测量出其延长线的夹角∠A的度数,你能帮他设计出方案吗?
D
C
E
F
A
A
G
G
1
2
问题情景
3
1.如图,已知AB‖ED, ∠ECF=65°,则∠FAB的度数为( )
A.115° B.65°
C.60° D.25°
A
夯实基础
2.如图,已知∠1=70° ,如果CD∥BE,那么∠B的度数为( )
A.70° B .100° C.110° D.120°
C
夯实基础
3. 下列图形中,由AB‖CD ,能得到∠1=∠2的是( )
B
夯实基础
4.如图,已知AG‖CF,AB‖CD,∠A=40°,求∠C的度数.
F
A
B
C
D
E
G
解 ∵AG∥CF( )
∴∠A=∠BEF( )
∵AB∥CD( )
∴∠C=∠BEF( )
∴∠A=∠C=400( )
已知
两直线平行,同位角相等
已知
两直线平行,同位角相等
等量代换
夯实基础
5、如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=50°,求∠EFC的度数
解 ∵∠1=500( )
∠1+∠DED'=1800( )
∴∠DED'=1300
∴∠D'EF=∠DEF=650
∵AD∥CBD( )
∴∠DEF+∠EFC=1800( )
∴∠EFC=1800-650=1150
已知
平角的定义
已知
两直线平行,内错角互补
夯实基础
如图,若AB//CD,求∠B、
∠D与∠BED的关系。
解:
过点E作EF//AB.
∴∠B=∠BEF ( )
∵AB∥CD( )
AB∥EF( )
∴EF∥CD( )
∴∠D=∠DEF( )
∴∠B+∠D=∠BEF+∠DEF=∠BED( )
两直线平行,内错角相等
已知
辅助线
平行于同一直线的两条直线也平行
两直线平行,内错角相等
等式的性质
A
B
C
D
E
F
能力提升
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课内反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
