2.3.3平行线的性质与判定综合应用 课件(共11张PPT)
文档属性
| 名称 | 2.3.3平行线的性质与判定综合应用 课件(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 10:26:42 | ||
图片预览



文档简介
(共11张PPT)
2.3 平行线的性质与
判定综合应用
北师版七(下)
a
c
b
平行线的性质与判定的综合
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
知识回顾
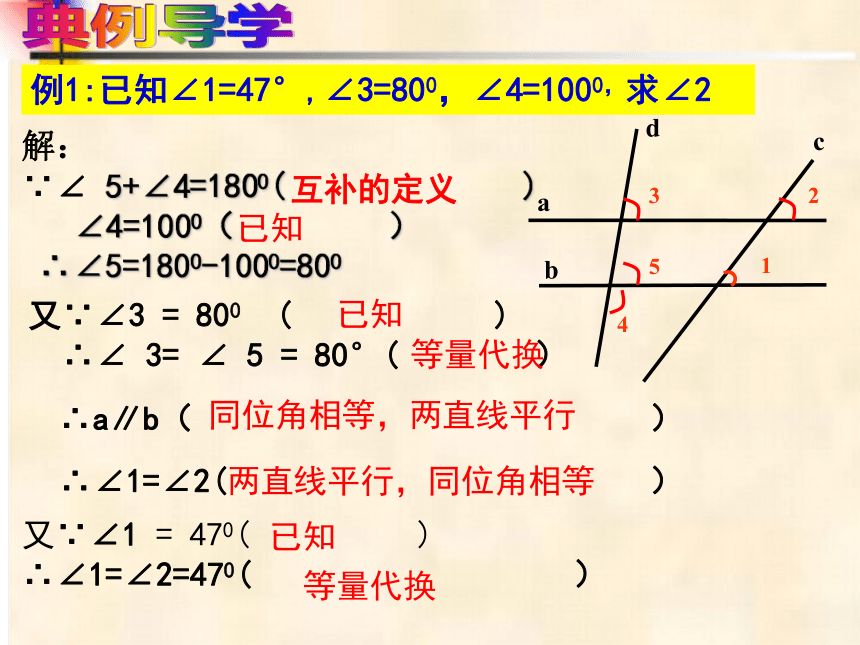
例1:已知∠1=47°,∠3=800,∠4=1000,求∠2
解:
∵∠ 5+∠4=1800( )
∠4=1000( )
∴∠5=1800-1000=800
又∵∠1 = 470( )
∴∠1=∠2=470( )
c
1
2
3
4
a
b
d
5
又∵∠3 = 800 ( )
∴∠ 3= ∠ 5 = 80°( )
∴a∥b( )
∴∠1=∠2( )
互补的定义
已知
已知
等量代换
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
典例导学
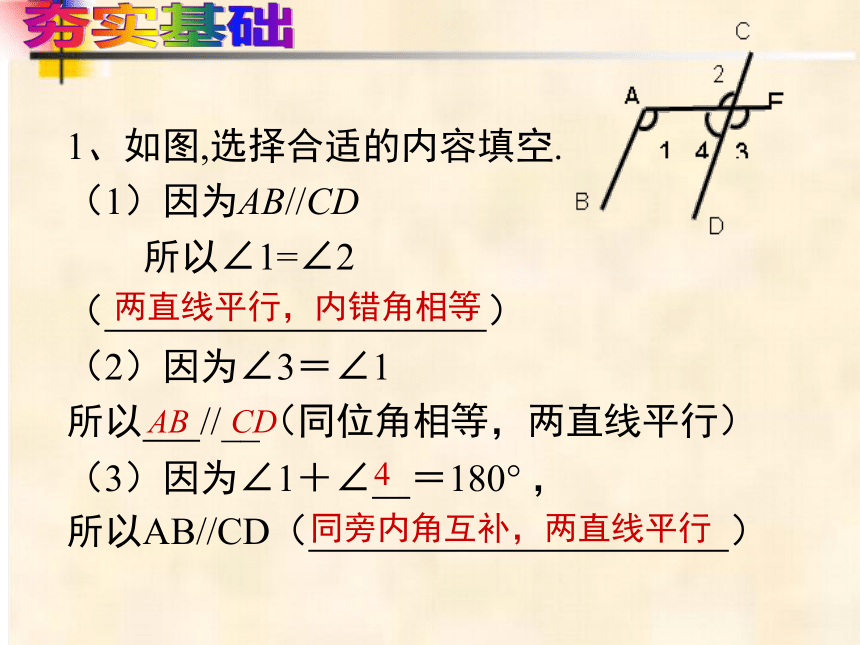
1、如图,选择合适的内容填空.
(1)因为AB//CD
所以∠1=∠2
( )
(2)因为∠3=∠1
所以 //__(同位角相等,两直线平行)
(3)因为∠1+∠ =180 ,
所以AB//CD( )
两直线平行,内错角相等
AB CD
4
同旁内角互补,两直线平行
夯实基础
2、如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线。
问:GH和MN平行吗?请说明理由。
夯实基础
解:
∵ AB∥CD( )
∴∠EGB=∠EMD( )
∵ GH平分∠EGB,MN平分∠EMD( )
∴∠EGH= ∠EGB,∠EMN= ∠EMD( )
∴∠EGH=∠EMN( )
∴GH∥MN( )
已知
两直线平行,同位角相等
已知
角平分线定义
等量代换
同位角相等,两直线平行
夯实基础
3、如图,∠AFE=∠ABC,∠1+∠2=180,
求证:BE∥AC.
证明:
∵∠AFE=∠ABC( )
∴EF∥BC( )
∴∠1=∠EBC( )
∵∠1+∠2=1800( )
∴∠EBC+∠2=1800( )
∴DC∥EB( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
已知
等量代换
同旁内角互补,两直线平行
夯实基础
1、如图,若∠B+∠D=∠BED,说明AB∥CD的理由。
解:
过点E作EF//AB.
∴∠B=∠BEF ( )
∵AB∥EF( )
∴ AB∥CD( )
∴EF∥CD( )
∴∠D=∠DEF( )
∵∠BED=∠B+∠D( )
∠BED=∠BEF+∠DEF
两直线平行,内错角相等
已知
已知
平行于同一直线的两条直线也平行
内错角相等,两直线平行
等式的性质
A
B
C
D
E
F
能力提升
2、当∠B、∠D、∠BED满足什么关系时,AB∥CD
解:∠B+∠D+∠BED=3600时,AB∥CD,理由如下:
过点E作EF//AB.
∴∠B+∠BEF=1800 ( )
∵AB∥EF( )
∴ AB∥CD( )
∴EF∥CD( )
∴∠D+∠DEF=1800( )
∵∠B+∠D+∠BED=3600( )
两直线平行,同旁内角互补
辅助线
已知
平行于同一直线的两条直线也平行
同旁内角互补,两直线平行
等式的性质
A
B
C
D
E
F
即∠B+∠D+∠BEF+∠DEF=3600
能力提升
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
课内反思
2.3 平行线的性质与
判定综合应用
北师版七(下)
a
c
b
平行线的性质与判定的综合
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
知识回顾
例1:已知∠1=47°,∠3=800,∠4=1000,求∠2
解:
∵∠ 5+∠4=1800( )
∠4=1000( )
∴∠5=1800-1000=800
又∵∠1 = 470( )
∴∠1=∠2=470( )
c
1
2
3
4
a
b
d
5
又∵∠3 = 800 ( )
∴∠ 3= ∠ 5 = 80°( )
∴a∥b( )
∴∠1=∠2( )
互补的定义
已知
已知
等量代换
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
典例导学
1、如图,选择合适的内容填空.
(1)因为AB//CD
所以∠1=∠2
( )
(2)因为∠3=∠1
所以 //__(同位角相等,两直线平行)
(3)因为∠1+∠ =180 ,
所以AB//CD( )
两直线平行,内错角相等
AB CD
4
同旁内角互补,两直线平行
夯实基础
2、如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线。
问:GH和MN平行吗?请说明理由。
夯实基础
解:
∵ AB∥CD( )
∴∠EGB=∠EMD( )
∵ GH平分∠EGB,MN平分∠EMD( )
∴∠EGH= ∠EGB,∠EMN= ∠EMD( )
∴∠EGH=∠EMN( )
∴GH∥MN( )
已知
两直线平行,同位角相等
已知
角平分线定义
等量代换
同位角相等,两直线平行
夯实基础
3、如图,∠AFE=∠ABC,∠1+∠2=180,
求证:BE∥AC.
证明:
∵∠AFE=∠ABC( )
∴EF∥BC( )
∴∠1=∠EBC( )
∵∠1+∠2=1800( )
∴∠EBC+∠2=1800( )
∴DC∥EB( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
已知
等量代换
同旁内角互补,两直线平行
夯实基础
1、如图,若∠B+∠D=∠BED,说明AB∥CD的理由。
解:
过点E作EF//AB.
∴∠B=∠BEF ( )
∵AB∥EF( )
∴ AB∥CD( )
∴EF∥CD( )
∴∠D=∠DEF( )
∵∠BED=∠B+∠D( )
∠BED=∠BEF+∠DEF
两直线平行,内错角相等
已知
已知
平行于同一直线的两条直线也平行
内错角相等,两直线平行
等式的性质
A
B
C
D
E
F
能力提升
2、当∠B、∠D、∠BED满足什么关系时,AB∥CD
解:∠B+∠D+∠BED=3600时,AB∥CD,理由如下:
过点E作EF//AB.
∴∠B+∠BEF=1800 ( )
∵AB∥EF( )
∴ AB∥CD( )
∴EF∥CD( )
∴∠D+∠DEF=1800( )
∵∠B+∠D+∠BED=3600( )
两直线平行,同旁内角互补
辅助线
已知
平行于同一直线的两条直线也平行
同旁内角互补,两直线平行
等式的性质
A
B
C
D
E
F
即∠B+∠D+∠BEF+∠DEF=3600
能力提升
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
课内反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
