2022年北师大版八年级数学下册 6.4 多边形内角和课件(18张)
文档属性
| 名称 | 2022年北师大版八年级数学下册 6.4 多边形内角和课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 14:52:40 | ||
图片预览





文档简介
(共18张PPT)
1. 小明有一个设想:2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能否实现
探索多边形的内角和
八年级下册第六章第四节
1、经历探索多边形内角和过程,进一步发展合 情推理能力。
2、掌握多边形的内角和的公式,进一步发展演绎推理能力。
3、会用内角和解决相应实际问题。
重点:多边形内角和定理的探索
难点:多边形内角和定理的应用
在平面内,由若干条不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。多边形的边、顶点、内角、内角和的含义与三角形相同。
1、什么是多边形以及什么是多边形的对角线?
在多边形中,连接不相邻的两顶
点的线段叫做多边形的对角线。
2、三角形内角和定理?
利用三角形知识探索任意四边形内角和
等于多少度?你最多能想到几种办法?
转化
思想
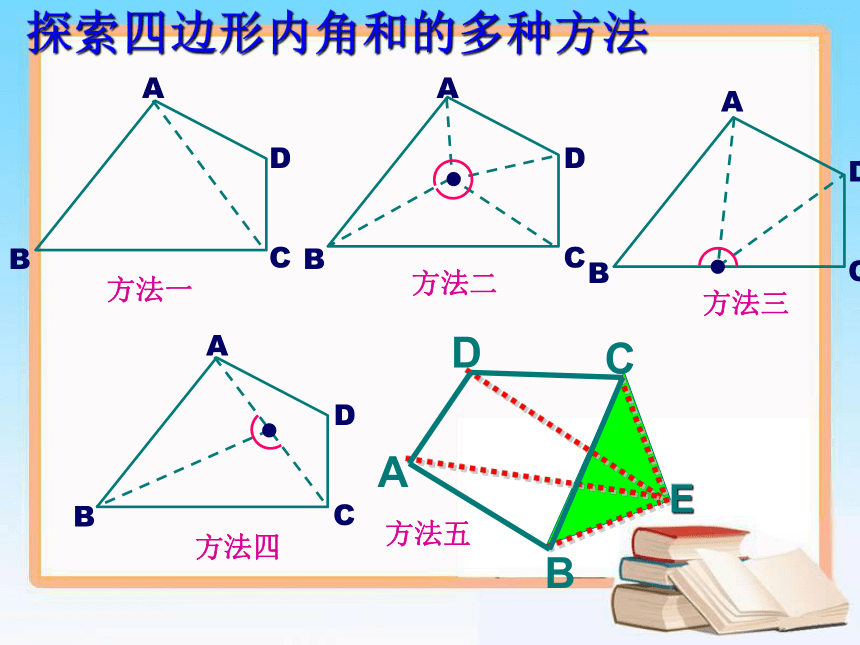
探索四边形内角和的多种方法
A
B
C
D
A
B
C
D
A
B
C
D
方法一
方法二
方法三
A
B
C
D
方法四
A
B
D
C
方法五
E
多边形边数
图形
从多边形的一个顶点引出的对角线条数
分割出三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
n-3
n-2
(n-2)·180
0
1
180
1
2
360
2
3
540
3
4
720
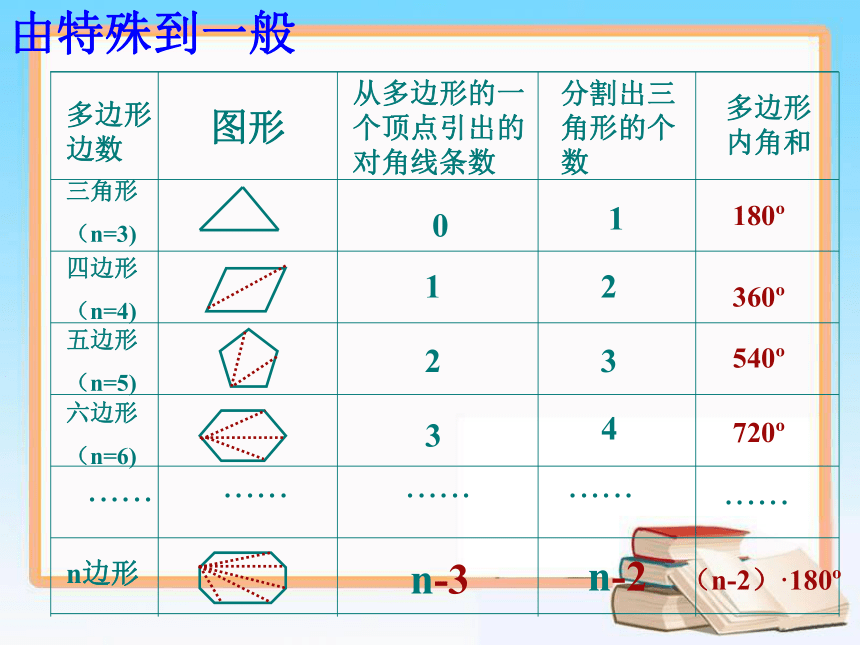
由特殊到一般
n边形的内角和等于(n-2)·180°
(n≥3)
多边形内角和定理
正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
60
90
120
108
135
正n边形的每一个内角是多少度
想一想:
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流。
议一议:
540
360
180
分类讨论思想
已知一个多边形的内角和是2340°,则这个多边形的边数是 。
15
解:设这个多边形的边数为n,根据题意,
得 (n-2) 180°= 2340°
n-2=13
n=15
方程
思想
所以,这个多边形的边数为15
1. 正十二边形的内角和______它的每一个内角是___.
2.多边形的边数增加一条,内角和就增加______。
180°
1800°
150°
3.小彬求出一个正多边形的一个内角为
145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由。
小明的想法不能实现,因为2008不能被180整除,那么多边形的边数就不是整数,而多边形的边数要求必须是大于或等于3的正整数。
1. 小明有一个设想:2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能否实现吗
1.多边形的内角和定理及其应用.
2.知道了多边形内角和的多种求解方法.
3.在探求过程中我们使用了观察、归纳、由一般到特殊的数学方法,并且运用了类比、转化和方程的数学思想。
A组:习题4.10 1、2、3 。
B组:如图,是桂林著名的日月双塔,它位于桂林市杉湖中心,两塔的每一层楼都是一个正多边形,已测得它的每一个内角为135 ,你能告诉我它的每一层楼是几边形吗
数学家华罗庚曾经说过: 宇宙之大, 粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
让我们热爱数学吧!并且学好数学,用数学创造更美好的生活.
2.如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
解:不合格.
理由:
∵五边形内角和为540°,
∴∠G= 540°-122°-155°-180°=83°≠80°
因此这个模板不合格。
1. 小明有一个设想:2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能否实现
探索多边形的内角和
八年级下册第六章第四节
1、经历探索多边形内角和过程,进一步发展合 情推理能力。
2、掌握多边形的内角和的公式,进一步发展演绎推理能力。
3、会用内角和解决相应实际问题。
重点:多边形内角和定理的探索
难点:多边形内角和定理的应用
在平面内,由若干条不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。多边形的边、顶点、内角、内角和的含义与三角形相同。
1、什么是多边形以及什么是多边形的对角线?
在多边形中,连接不相邻的两顶
点的线段叫做多边形的对角线。
2、三角形内角和定理?
利用三角形知识探索任意四边形内角和
等于多少度?你最多能想到几种办法?
转化
思想
探索四边形内角和的多种方法
A
B
C
D
A
B
C
D
A
B
C
D
方法一
方法二
方法三
A
B
C
D
方法四
A
B
D
C
方法五
E
多边形边数
图形
从多边形的一个顶点引出的对角线条数
分割出三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
n-3
n-2
(n-2)·180
0
1
180
1
2
360
2
3
540
3
4
720
由特殊到一般
n边形的内角和等于(n-2)·180°
(n≥3)
多边形内角和定理
正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
60
90
120
108
135
正n边形的每一个内角是多少度
想一想:
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流。
议一议:
540
360
180
分类讨论思想
已知一个多边形的内角和是2340°,则这个多边形的边数是 。
15
解:设这个多边形的边数为n,根据题意,
得 (n-2) 180°= 2340°
n-2=13
n=15
方程
思想
所以,这个多边形的边数为15
1. 正十二边形的内角和______它的每一个内角是___.
2.多边形的边数增加一条,内角和就增加______。
180°
1800°
150°
3.小彬求出一个正多边形的一个内角为
145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由。
小明的想法不能实现,因为2008不能被180整除,那么多边形的边数就不是整数,而多边形的边数要求必须是大于或等于3的正整数。
1. 小明有一个设想:2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能否实现吗
1.多边形的内角和定理及其应用.
2.知道了多边形内角和的多种求解方法.
3.在探求过程中我们使用了观察、归纳、由一般到特殊的数学方法,并且运用了类比、转化和方程的数学思想。
A组:习题4.10 1、2、3 。
B组:如图,是桂林著名的日月双塔,它位于桂林市杉湖中心,两塔的每一层楼都是一个正多边形,已测得它的每一个内角为135 ,你能告诉我它的每一层楼是几边形吗
数学家华罗庚曾经说过: 宇宙之大, 粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
让我们热爱数学吧!并且学好数学,用数学创造更美好的生活.
2.如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
解:不合格.
理由:
∵五边形内角和为540°,
∴∠G= 540°-122°-155°-180°=83°≠80°
因此这个模板不合格。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
