2022年北师大版八年级数学下册 1.1 等腰三角形与等边三角形的性质课件(30张)
文档属性
| 名称 | 2022年北师大版八年级数学下册 1.1 等腰三角形与等边三角形的性质课件(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
等腰三角形与等边三角形的性质(1)
八年级下
创设情景,激发兴趣
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
回顾定义,引出新知
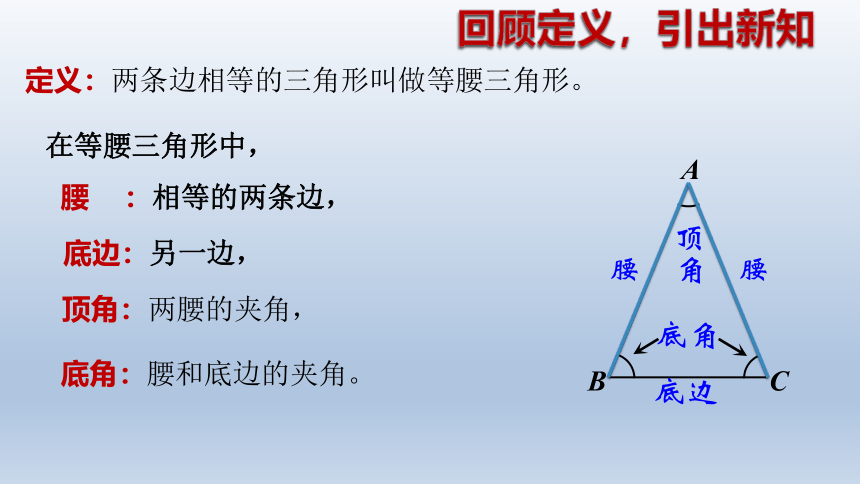
定义:两条边相等的三角形叫做等腰三角形。
底角:腰和底边的夹角。
在等腰三角形中,
腰 :相等的两条边,
底边:另一边,
顶角:两腰的夹角,
A
B
C
底边
腰
腰
顶角
底角
数学实验室
实践探索,感受特征
请拿出一张长方形的纸片,试一试,通过折叠一次,剪一条线,是否可以剪出一个等腰三角形呢?
等腰三角形是轴对称图形
A
B
C
D
实践探索,感受交流
D
A
B
C
重合的角
重合的线段
观察你所得到等腰三角形,
你发现等腰三角形具有哪些特征?
证明探索
证明两个角相等有什么常见的方法:
两个三角形全等
如何构造两个全等的三角形?
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有BD=CD
D
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌△ACD
(SSS)
∴ ∠B=∠C,
(全等三角形对应角相等)
作底边BC边上的中线AD
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有
D
在RT△ABD和RT△ACD中
AB=AC
AD=AD
(公共边)
∴ △ABD≌△ACD
(HL)
∴ ∠B=∠C,
(全等三角形对应角相等)
作AD BC于点D
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有
D
在△ABD和△ACD中
AB=AC
AD=AD
(公共边)
∴ △ABD≌△ACD
(SAS)
∴ ∠B=∠C,
(全等三角形对应角相等)
作AD平分 交BC于点D
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
创设情景,激发兴趣
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
解决问题
C
证明:
∵ ΔABC是等腰三角形,
∴ AB = AC,
∵ D为BC的中点,
∵ AD⊥地面
∴ BC平行于地面
你懂了吗?
已知:ΔABC是等腰三角形,AB=AC,D为BC的中点,
求证:BC平行于地面。
A
D
B
∴ AD⊥BC(等腰三角形三线合一)
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
等腰三角形ABC 中,AB=AC
基础训练
A
B
C
(1)若 ,则 度。
(2)若一个角为80度 ,则 度。
(3)若 ,则 度。
80
80或50
72
如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
解∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
综合训练
A
B
C
D
性质3:等边对等角
(等腰三角形的两个底角相等)
性质4:三线合一
(顶角平分线、底边上的中线、底边上的高线相互重合)
性质2:轴对称图形
性质1:两腰相等
回顾小结,整体感知
A
B
C
D
E
2:奇妙的旅行(选做)
已知:AB=AC AD=AE
求证:BD=CE
你有多少奇妙的想法?
作业布置 课后延伸
1:课本P77练习1,2,3
谢 谢!
A
B
C
D
E
证明一:
A
B
C
D
E
证明二:
A
B
C
D
E
F
证明三:
作
于F点
等腰三角形与等边三角形的性质(1)
八年级下
创设情景,激发兴趣
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
回顾定义,引出新知
定义:两条边相等的三角形叫做等腰三角形。
底角:腰和底边的夹角。
在等腰三角形中,
腰 :相等的两条边,
底边:另一边,
顶角:两腰的夹角,
A
B
C
底边
腰
腰
顶角
底角
数学实验室
实践探索,感受特征
请拿出一张长方形的纸片,试一试,通过折叠一次,剪一条线,是否可以剪出一个等腰三角形呢?
等腰三角形是轴对称图形
A
B
C
D
实践探索,感受交流
D
A
B
C
重合的角
重合的线段
观察你所得到等腰三角形,
你发现等腰三角形具有哪些特征?
证明探索
证明两个角相等有什么常见的方法:
两个三角形全等
如何构造两个全等的三角形?
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有BD=CD
D
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌△ACD
(SSS)
∴ ∠B=∠C,
(全等三角形对应角相等)
作底边BC边上的中线AD
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有
D
在RT△ABD和RT△ACD中
AB=AC
AD=AD
(公共边)
∴ △ABD≌△ACD
(HL)
∴ ∠B=∠C,
(全等三角形对应角相等)
作AD BC于点D
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
已知:△ABC中,AB=AC,求证:∠B=∠C。
证明:
A
B
C
则有
D
在△ABD和△ACD中
AB=AC
AD=AD
(公共边)
∴ △ABD≌△ACD
(SAS)
∴ ∠B=∠C,
(全等三角形对应角相等)
作AD平分 交BC于点D
∠ADB=∠ADC,∠BAD=∠CAD
∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
∴ AD⊥BC
┌
创设情景,激发兴趣
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
解决问题
C
证明:
∵ ΔABC是等腰三角形,
∴ AB = AC,
∵ D为BC的中点,
∵ AD⊥地面
∴ BC平行于地面
你懂了吗?
已知:ΔABC是等腰三角形,AB=AC,D为BC的中点,
求证:BC平行于地面。
A
D
B
∴ AD⊥BC(等腰三角形三线合一)
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗
等腰三角形ABC 中,AB=AC
基础训练
A
B
C
(1)若 ,则 度。
(2)若一个角为80度 ,则 度。
(3)若 ,则 度。
80
80或50
72
如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
解∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
综合训练
A
B
C
D
性质3:等边对等角
(等腰三角形的两个底角相等)
性质4:三线合一
(顶角平分线、底边上的中线、底边上的高线相互重合)
性质2:轴对称图形
性质1:两腰相等
回顾小结,整体感知
A
B
C
D
E
2:奇妙的旅行(选做)
已知:AB=AC AD=AE
求证:BD=CE
你有多少奇妙的想法?
作业布置 课后延伸
1:课本P77练习1,2,3
谢 谢!
A
B
C
D
E
证明一:
A
B
C
D
E
证明二:
A
B
C
D
E
F
证明三:
作
于F点
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
