1.1.2 与等腰三角形有关的线段的性质与等边三角形的性质(共24张PPT)
文档属性
| 名称 | 1.1.2 与等腰三角形有关的线段的性质与等边三角形的性质(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
1 等腰三角形
第2课时 与等腰三角形有关的线段的性质与等边三角形的性质
学习目标
1.经历“探索—发现—猜想—证明”的过程,逐步掌握综合证明的方法,发展推理能力;
2.能证明等腰(等边)三角形的性质定理.
情境引入
小故事 大智慧
推理证明很重要哦!
忆一忆
等腰三角形的性质:
两底角相等(等边对等角)
顶角的平分线、底边上高线、底边上中线互相重合(三线合一)
D
探究新知
请你在等腰三角形中画出一些线段(如角平分线、中线、高等),
你能发现其中一些相等的线段吗?
你能说明你的结论是正确的吗?
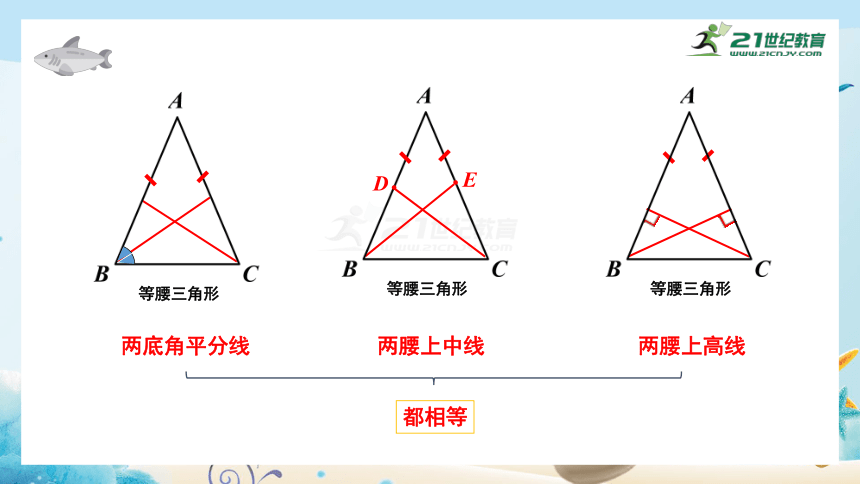
等腰三角形
两底角平分线
等腰三角形
两腰上中线
都相等
D
.
E
.
等腰三角形
两腰上高线
典型例题
例1 证明:等腰三角形两底角的平分线相等.
条件
结论
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
等腰三角形
D
E
典型例题
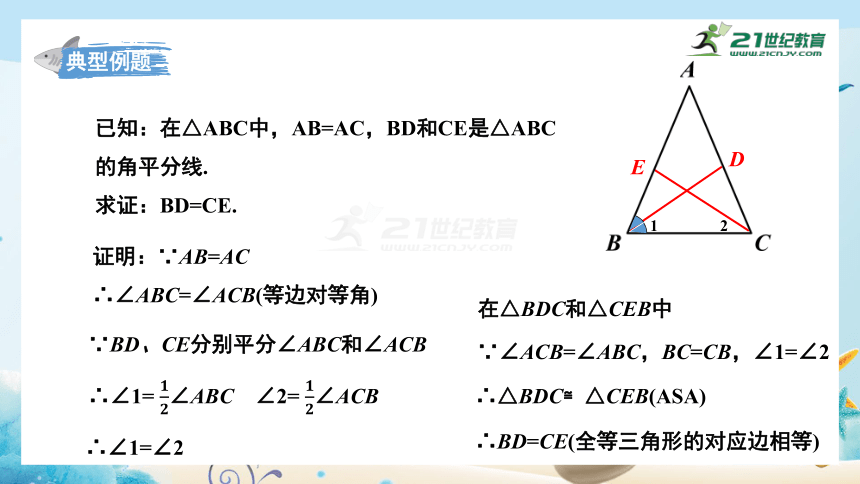
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
1
D
E
2
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB
∴∠1= ∠ABC ∠2= ∠ACB
在△BDC和△CEB中
∵∠ACB=∠ABC,BC=CB,∠1=∠2
∴∠1=∠2
∴△BDC≌△CEB(ASA)
∴BD=CE(全等三角形的对应边相等)
典型例题
证法2:∵AB=AC,∴∠ABC=∠ACB
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ,∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
3
D
E
4
一题多解
例1 证明:等腰三角形两底角的平分线相等.
条件
结论
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
D
E
找
典型例题
画
写
证
文字语言
符号语言
图形语言
拓展提升
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB, 那么BD=CE吗
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
3
D
E
4
(2)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢
那么BD=CE吗
(3)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢
那么BD=CE吗
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
拓展提升
3
D
E
4
由此,你得到什么结论?
等腰三角形两底角的对应n等分线相等
上述的研究过程你得到什么启发?
一般
特殊
思想方法
例2 证明:等腰三角形两腰上的中线相等.
已知:在△ABC中,AB=AC,BD、CE是△ABC的中线.
求证:BD=CE.
等腰三角形
D
E
证明:在△ABC中,AB=AC
∵BD、CE是△ABC的中线
∴AD= AC ,AE= AB
∴AD=AE
在△ADB和△AEC中,
∵AB=AC,∠A=∠A,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE(全等三角形的对应边相等)
类比探究
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
D
E
类比探究
如果AD= AC,AE= AB,那么BD=CE吗
如果AD= AC,AE= AB呢
由此,你能得到什么结论
等腰三角形两腰上对应n等分线相等
“等腰三角形两腰上的高线相等”这个怎么证明呢?
等边三角形作为特殊的等腰三角形,它又会有怎样的性质呢?
类比探究
三边相等
三个内角相等,每个内角都等于60°
等边三角形的三个内角都相等,并且每个角都等于60.
已知:如图所示,在△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°.
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
又∵AC=BC(已知)
∴∠A=∠B(等边对等角)
∴∠A=∠B =∠C
在△ABC中
∵∠A+∠B +∠C=180°
∴ ∠A=∠B=∠C=60°
证明:
定理
类比探究
边:三边相等
角:三个内角相等,每个内角都等于60°
重要线段:
(1):每边上“三线合一”
(2):三内角平分线、三边中线、三条高线都相等
等边三角形作为特殊的等腰三角形,它又会有怎样的性质呢?
类比探究
求等边三角形两条中线相交所成锐角的度数.
O
已知: 在△ABC中,AB=AC=BC,△ABC的中线AD、BE相交于点O.
求∠BOD的度数.
解: 在△ABC中,
∵AB=AC=BC,AD、BE是△ABC的中线
∴AD⊥BC,BE平分∠ABC
∴∠ADB=90°,∠OBD= ∠ABC=30°(三线合一)
∴∠BOD=903060
练一练
D
E
课堂小结
知识
1.等腰三角形中对应线段相等
2.等边三角形性质:边、角、重要线段
等腰三角形
方法
1.命题四步法:找、画、写、证
2.几何证明: 执果索因、由因导果
数学
思想
1.转化 “三种”语言转化”
2.“特殊”—“一般”
课后作业
1. 完成学案A组、B组习题.
2. 拓展作业:对本节课探索问题的方式方法,你印象最深的是什么?自我归纳小结,选取一种并查找相关资料,形成一份手抄报.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1 等腰三角形
第2课时 与等腰三角形有关的线段的性质与等边三角形的性质
学习目标
1.经历“探索—发现—猜想—证明”的过程,逐步掌握综合证明的方法,发展推理能力;
2.能证明等腰(等边)三角形的性质定理.
情境引入
小故事 大智慧
推理证明很重要哦!
忆一忆
等腰三角形的性质:
两底角相等(等边对等角)
顶角的平分线、底边上高线、底边上中线互相重合(三线合一)
D
探究新知
请你在等腰三角形中画出一些线段(如角平分线、中线、高等),
你能发现其中一些相等的线段吗?
你能说明你的结论是正确的吗?
等腰三角形
两底角平分线
等腰三角形
两腰上中线
都相等
D
.
E
.
等腰三角形
两腰上高线
典型例题
例1 证明:等腰三角形两底角的平分线相等.
条件
结论
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
等腰三角形
D
E
典型例题
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
1
D
E
2
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB
∴∠1= ∠ABC ∠2= ∠ACB
在△BDC和△CEB中
∵∠ACB=∠ABC,BC=CB,∠1=∠2
∴∠1=∠2
∴△BDC≌△CEB(ASA)
∴BD=CE(全等三角形的对应边相等)
典型例题
证法2:∵AB=AC,∴∠ABC=∠ACB
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ,∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
3
D
E
4
一题多解
例1 证明:等腰三角形两底角的平分线相等.
条件
结论
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE.
D
E
找
典型例题
画
写
证
文字语言
符号语言
图形语言
拓展提升
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB, 那么BD=CE吗
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
3
D
E
4
(2)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢
那么BD=CE吗
(3)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢
那么BD=CE吗
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
拓展提升
3
D
E
4
由此,你得到什么结论?
等腰三角形两底角的对应n等分线相等
上述的研究过程你得到什么启发?
一般
特殊
思想方法
例2 证明:等腰三角形两腰上的中线相等.
已知:在△ABC中,AB=AC,BD、CE是△ABC的中线.
求证:BD=CE.
等腰三角形
D
E
证明:在△ABC中,AB=AC
∵BD、CE是△ABC的中线
∴AD= AC ,AE= AB
∴AD=AE
在△ADB和△AEC中,
∵AB=AC,∠A=∠A,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE(全等三角形的对应边相等)
类比探究
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
D
E
类比探究
如果AD= AC,AE= AB,那么BD=CE吗
如果AD= AC,AE= AB呢
由此,你能得到什么结论
等腰三角形两腰上对应n等分线相等
“等腰三角形两腰上的高线相等”这个怎么证明呢?
等边三角形作为特殊的等腰三角形,它又会有怎样的性质呢?
类比探究
三边相等
三个内角相等,每个内角都等于60°
等边三角形的三个内角都相等,并且每个角都等于60.
已知:如图所示,在△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°.
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
又∵AC=BC(已知)
∴∠A=∠B(等边对等角)
∴∠A=∠B =∠C
在△ABC中
∵∠A+∠B +∠C=180°
∴ ∠A=∠B=∠C=60°
证明:
定理
类比探究
边:三边相等
角:三个内角相等,每个内角都等于60°
重要线段:
(1):每边上“三线合一”
(2):三内角平分线、三边中线、三条高线都相等
等边三角形作为特殊的等腰三角形,它又会有怎样的性质呢?
类比探究
求等边三角形两条中线相交所成锐角的度数.
O
已知: 在△ABC中,AB=AC=BC,△ABC的中线AD、BE相交于点O.
求∠BOD的度数.
解: 在△ABC中,
∵AB=AC=BC,AD、BE是△ABC的中线
∴AD⊥BC,BE平分∠ABC
∴∠ADB=90°,∠OBD= ∠ABC=30°(三线合一)
∴∠BOD=903060
练一练
D
E
课堂小结
知识
1.等腰三角形中对应线段相等
2.等边三角形性质:边、角、重要线段
等腰三角形
方法
1.命题四步法:找、画、写、证
2.几何证明: 执果索因、由因导果
数学
思想
1.转化 “三种”语言转化”
2.“特殊”—“一般”
课后作业
1. 完成学案A组、B组习题.
2. 拓展作业:对本节课探索问题的方式方法,你印象最深的是什么?自我归纳小结,选取一种并查找相关资料,形成一份手抄报.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
