3.4实际问题与一元一次方程--工程问题
文档属性
| 名称 | 3.4实际问题与一元一次方程--工程问题 |  | |
| 格式 | zip | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-29 14:34:27 | ||
图片预览





文档简介
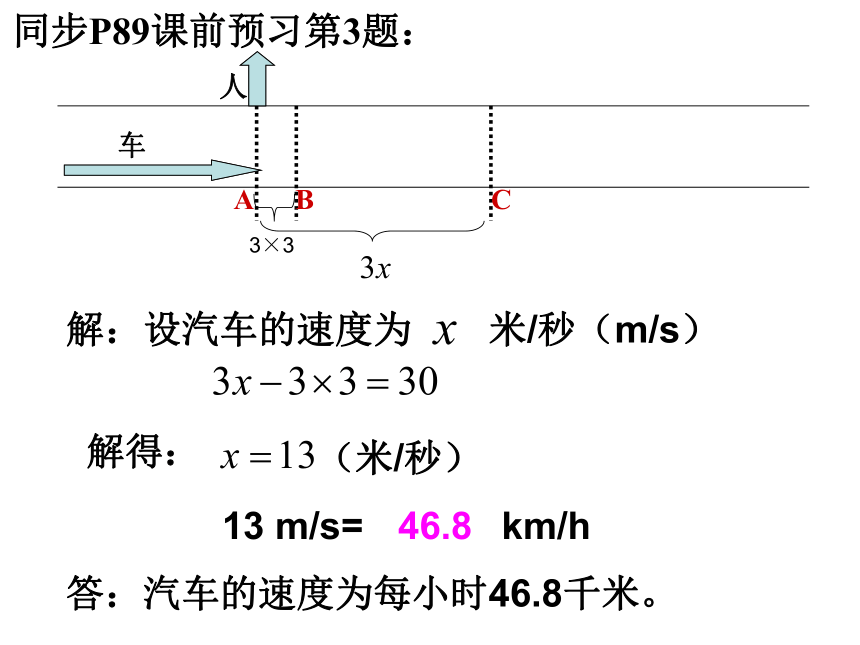
课件13张PPT。3.4实际问题与一元一次方程工程问题复习巩固上节课我们学习了什么知识?列一元一次方程解决实际问题中的分配(配套)问题解决这类问题应注意什么?1、充分理解配套的含义;2、调配前后的变化,弄清变化后的数量关系;3、恰当的设未知数,从调配后的数量关系中找等量关系。3×3解:设汽车的速度为 米/秒(m/s)解得:(米/秒)13 m/s= km/h 46.8答:汽车的速度为每小时46.8千米。同步P89课前预习第3题:A人车做某件工作,甲单独做要8时才能完成,乙单独做要12时才能完成,想一想:
①甲做1时完成全部工作量的几分之几?_____ 。
②乙做1时完成全部工作量的几分之几?_____ 。
③甲、乙合做1时完成全部工作量的几分之几?_____ 。
④甲做x时完成的工作量是_____。
⑤甲、乙合做x小时完成的工作量是___。探究:甲的工作效率乙的工作效率工作量=工作效率×工作时间思考:(1)两人合作32小时完成对吗?为什么?
(2)甲每小时完成全部工作的 ;
乙每小时完成全部工作的 ;甲x小时
完成全部工作的 ;乙x小时完成全部
工作的 。一件工作,甲单独做20小时完成,乙单独做12小时完成。那么两人合作多少小时完成?试一试(1)人均效率(一个人做一小时的工作量)是
。
(2)这项工作由8人来做,x小时完成的工作量
是 。
总结:一个工作由m个人n小时完成,那么人均效率是 。2、一项工作,12个人4个小时才能完成。若这项工作由8个人来做,要多少小时才能完成呢?回顾以上过程,可以发现:工作量=人均效率 × 人数 ×时间 这是计算工作量的常用数量关系式.例2
整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?分析:如果把总工作量设为1,
则人均效率(一个人1 h 完成的工作量)为 ,
人先做4 h 完成的工作量为 ,
这两个工作量之和应等于总工作量.例2、整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?增加2人后再做8 h 完成的工作量为 ,解:设安排 人先做4 h .根据先后两个时段的工作量之和应等于总工作
量,列出方程解方程,得答:应安排2人先做4 h .例2、整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?列方程解应用题的一般步骤 1、审题:分析题意,找出题中关键词及数量关系。
2、设元:选择一个适当的未知数用字母表示。 3、列方程:根据等量关系列出方程; 4、解方程,求出未知数的值; 小结5、检验并作答:检验求得的值是否正确、合理;写出答案。设、列、解、检、答练一练解:设两队同时施工 天可以铺好。
依题意得:课本P101练习第2题解方程,得答:两队同时施工8天可以铺好。作业:课本P106习题3.4第4、5题家庭作业(周六、周日):
同步学习P89——P90
一张数学试卷
①甲做1时完成全部工作量的几分之几?_____ 。
②乙做1时完成全部工作量的几分之几?_____ 。
③甲、乙合做1时完成全部工作量的几分之几?_____ 。
④甲做x时完成的工作量是_____。
⑤甲、乙合做x小时完成的工作量是___。探究:甲的工作效率乙的工作效率工作量=工作效率×工作时间思考:(1)两人合作32小时完成对吗?为什么?
(2)甲每小时完成全部工作的 ;
乙每小时完成全部工作的 ;甲x小时
完成全部工作的 ;乙x小时完成全部
工作的 。一件工作,甲单独做20小时完成,乙单独做12小时完成。那么两人合作多少小时完成?试一试(1)人均效率(一个人做一小时的工作量)是
。
(2)这项工作由8人来做,x小时完成的工作量
是 。
总结:一个工作由m个人n小时完成,那么人均效率是 。2、一项工作,12个人4个小时才能完成。若这项工作由8个人来做,要多少小时才能完成呢?回顾以上过程,可以发现:工作量=人均效率 × 人数 ×时间 这是计算工作量的常用数量关系式.例2
整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?分析:如果把总工作量设为1,
则人均效率(一个人1 h 完成的工作量)为 ,
人先做4 h 完成的工作量为 ,
这两个工作量之和应等于总工作量.例2、整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?增加2人后再做8 h 完成的工作量为 ,解:设安排 人先做4 h .根据先后两个时段的工作量之和应等于总工作
量,列出方程解方程,得答:应安排2人先做4 h .例2、整理一批图书,由一个人做要40 h 完成. 现计划由一部分人先做4 h ,然后增加2人与他们一起做8 h ,完成这项工作假设这些人的工作效率相同,具体应先安排多少人工作?列方程解应用题的一般步骤 1、审题:分析题意,找出题中关键词及数量关系。
2、设元:选择一个适当的未知数用字母表示。 3、列方程:根据等量关系列出方程; 4、解方程,求出未知数的值; 小结5、检验并作答:检验求得的值是否正确、合理;写出答案。设、列、解、检、答练一练解:设两队同时施工 天可以铺好。
依题意得:课本P101练习第2题解方程,得答:两队同时施工8天可以铺好。作业:课本P106习题3.4第4、5题家庭作业(周六、周日):
同步学习P89——P90
一张数学试卷
