数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质(共12张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质(共12张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 314.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 09:55:53 | ||
图片预览




文档简介
(共12张PPT)
6.3.2二项式系数的性质
一、教学目标
1.理解和掌握二项式系数的性质,并会简单的应用;
2.初步了解用赋值法是解决二项式系数问题;
3.能用函数的观点分析处理二项式系数的性质,提高分析问题和解决问题的能力 学习
一般地,对于n N*有
二项定理:
二项展开式中的二项式系数指的是那些?共有多少个?
下面我们来研究二项式系数有些什么性质?
二、问题导学
探究
用计算工具计算(a+b)n的展开式的二项式系数,并填入表6.3-1
n (a+b)n的展开式的二项式系数
1
2
3
4
5
6
通过计算、填表,你发现了什么规律?
展开式中的二项式系数,如下表所示:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
…… …… ……
二、问题导学
从表6.3.1可以发现,每一行中的系数具有对称性,除此之处还有什么规律呢?便于发现规律,上表还可以写成如下图的形式
图6.3.1
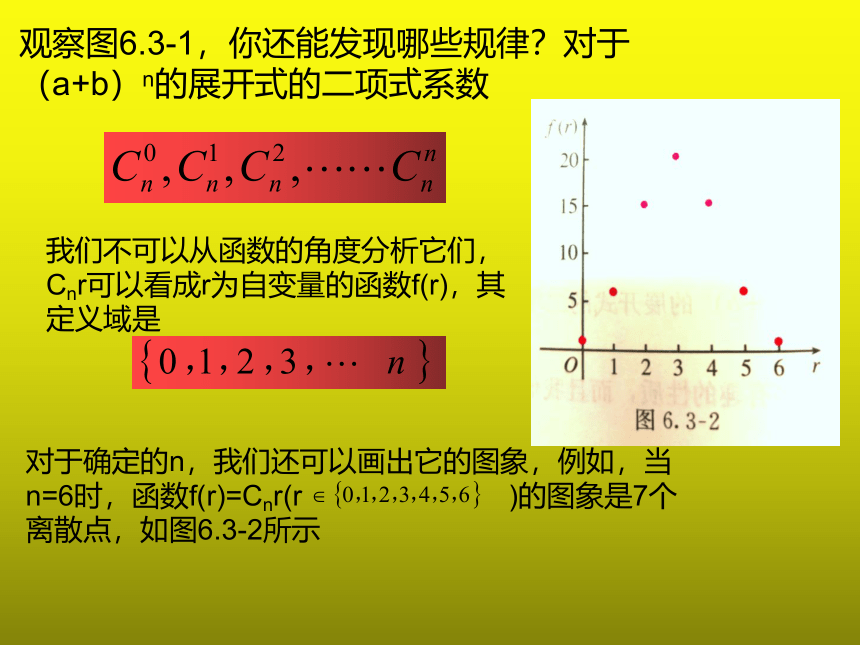
观察图6.3-1,你还能发现哪些规律?对于(a+b)n的展开式的二项式系数
我们不可以从函数的角度分析它们,Cnr可以看成r为自变量的函数f(r),其定义域是
对于确定的n,我们还可以画出它的图象,例如,当n=6时,函数f(r)=Cnr(r )的图象是7个离散点,如图6.3-2所示
探究
(1)观察6.3-2,你发现了什么规律?
(2)请你分别画出n=7,8,9时函数f(r)=Cnr的图象,比较它们的异同,你发现了什么规律?
(1)对称性:
与首末两端“等距离”的两个二项式系数相等.
(2)增减性与最大值.
增减性的实质是比较 的大小.
从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.
(3)各二项式系数的和.
课本例3:试证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
即证:
证明:在展开式 中
令a=1,b=-1得
启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。
三、点拨精讲
四、课堂小结:
1.当n 10时常用杨辉三角处理二项式系数问题;
2.利用函数图象可得二项式系数的对称性、增减性和最大值;
3.常用赋值法解决二项式系数问题.
1.(1﹣x )13 的展开式中系数最小的项是 ( ) (A)第六项 (B)第七项 (C)第八项 (D)第九项
C
2.求证:
五、当堂训练
证明:∵
倒序相加法
6.3.2二项式系数的性质
一、教学目标
1.理解和掌握二项式系数的性质,并会简单的应用;
2.初步了解用赋值法是解决二项式系数问题;
3.能用函数的观点分析处理二项式系数的性质,提高分析问题和解决问题的能力 学习
一般地,对于n N*有
二项定理:
二项展开式中的二项式系数指的是那些?共有多少个?
下面我们来研究二项式系数有些什么性质?
二、问题导学
探究
用计算工具计算(a+b)n的展开式的二项式系数,并填入表6.3-1
n (a+b)n的展开式的二项式系数
1
2
3
4
5
6
通过计算、填表,你发现了什么规律?
展开式中的二项式系数,如下表所示:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
…… …… ……
二、问题导学
从表6.3.1可以发现,每一行中的系数具有对称性,除此之处还有什么规律呢?便于发现规律,上表还可以写成如下图的形式
图6.3.1
观察图6.3-1,你还能发现哪些规律?对于(a+b)n的展开式的二项式系数
我们不可以从函数的角度分析它们,Cnr可以看成r为自变量的函数f(r),其定义域是
对于确定的n,我们还可以画出它的图象,例如,当n=6时,函数f(r)=Cnr(r )的图象是7个离散点,如图6.3-2所示
探究
(1)观察6.3-2,你发现了什么规律?
(2)请你分别画出n=7,8,9时函数f(r)=Cnr的图象,比较它们的异同,你发现了什么规律?
(1)对称性:
与首末两端“等距离”的两个二项式系数相等.
(2)增减性与最大值.
增减性的实质是比较 的大小.
从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.
(3)各二项式系数的和.
课本例3:试证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
即证:
证明:在展开式 中
令a=1,b=-1得
启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。
三、点拨精讲
四、课堂小结:
1.当n 10时常用杨辉三角处理二项式系数问题;
2.利用函数图象可得二项式系数的对称性、增减性和最大值;
3.常用赋值法解决二项式系数问题.
1.(1﹣x )13 的展开式中系数最小的项是 ( ) (A)第六项 (B)第七项 (C)第八项 (D)第九项
C
2.求证:
五、当堂训练
证明:∵
倒序相加法
