北师大版八年级数学下册 1.3 线段垂直平分线的性质 课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 1.3 线段垂直平分线的性质 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 17:17:48 | ||
图片预览



文档简介
(共15张PPT)
第2课时 线段垂直平分线的性质
A
C
E
B
D
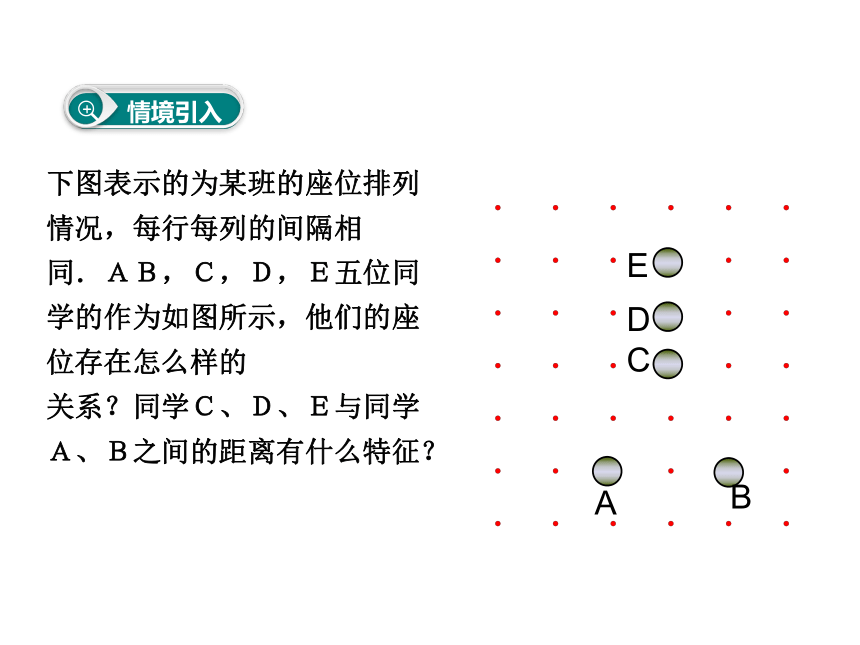
下图表示的为某班的座位排列情况,每行每列的间隔相同.AB,C,D,E五位同学的作为如图所示,他们的座位存在怎么样的
关系?同学C、D、E与同学A、B之间的距离有什么特征?
情境引入
M
N
A
C
E
B
D
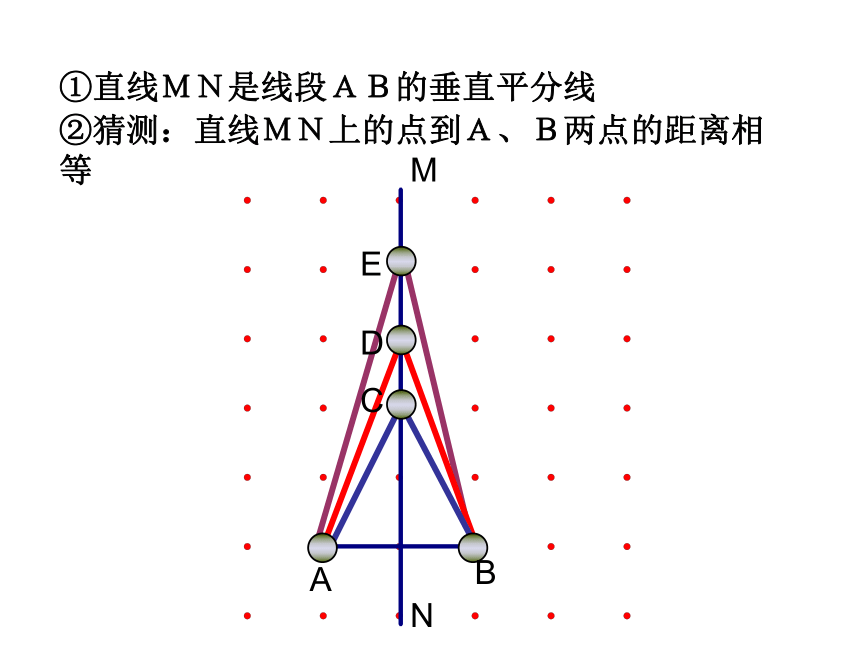
①直线MN是线段AB的垂直平分线
②猜测:直线MN上的点到A、B两点的距离相等
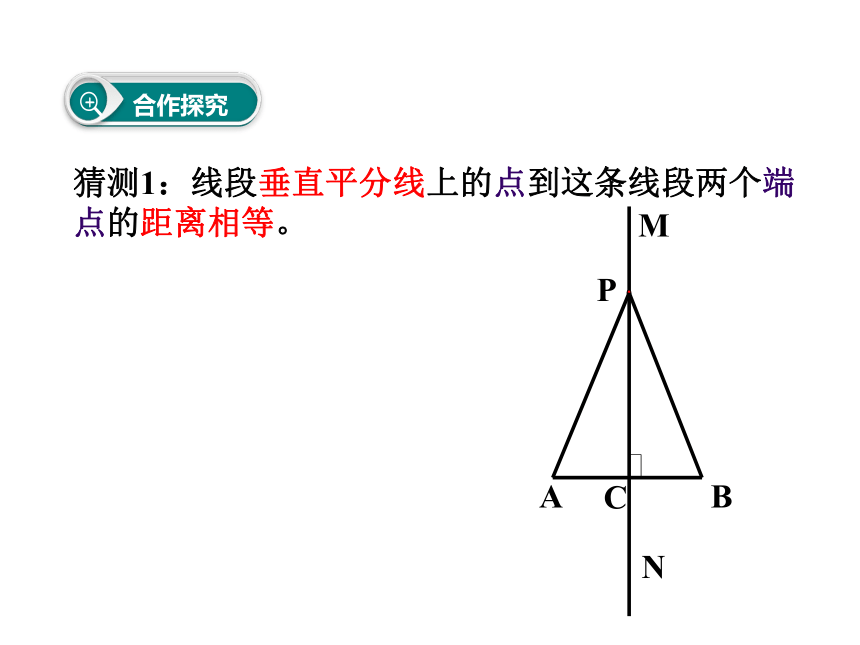
猜测1:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
C
合作探究
已知:如图,直线MN⊥线段AB,垂足为C, 且AC=CB.
求证:PA=PB
A
B
P
M
N
C
证明:∵ MN⊥AB 于点C (已知),
∴ ∠PCA= ∠PCB=90°(垂直的定义).
在 △PAC和△PBC中,
AC=BC(已知),
∠PCA= ∠PCB(已证),
PC=PC(公共边)
∴ △PAC ≌△ PBC(SAS).
∴PA=PB(全等三角形的对应边相等).
定理:线段垂直平分线上的点到这条线段两个
端点的距离相等。
A
B
P
M
N
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点和这条线段两个端点的距离相等
A
B
P
M
N
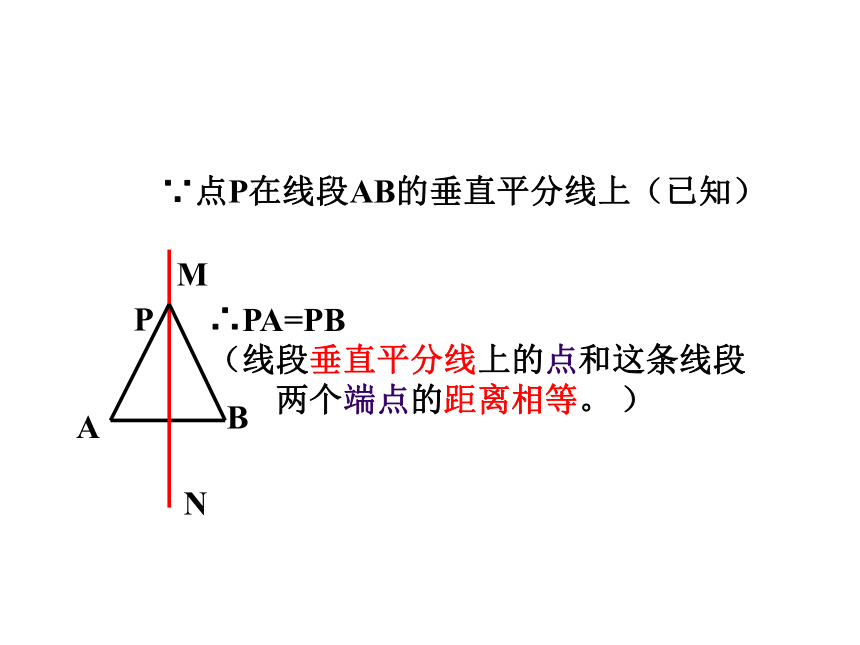
∵点P在线段AB的垂直平分线上(已知)
∴PA=PB
(线段垂直平分线上的点和这条线段
两个端点的距离相等。 )
猜测2:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
已知:如图,PA=PB
求证:P在AB的垂直平分线上
证明:过P点作MN⊥AB,垂足为C
∵PA=PB(已知)
∴AC=BC
(等腰三角形的“三线合一”)
A
B
P
M
N
C
∴ MN是AB的垂直平分线
∴P在AB的垂直平分线上
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
点P在线段AB的垂直平分线上
PA=PB
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
点P在线段AB的垂直平分线上
∵ PA=PB(已知)
∴点P在线段AB的垂直平分线上
(和一条线段两个端点
距离相等的点,在这条线段
的垂直平分线上)
A
B
P
M
N
例1 已知:如图,AB=AC=8cm ,DE是AB边的中垂线
交AC于点E,BC=6cm,求△BEC的周长
证明: ∵ DE是AB边的中垂线 (已知),
∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴AE+EC=BE+EC=8cm
(等式性质).
∵AC=8cm(已知),
∴ C△BEC=BE+EC+BC
=8+6=14cm
又∵ BC=6cm(已知)
有垂直平分线,就有等腰三角形的产生
例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
B
A
C
D
E
F
G
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
题型转换:证明三角形的三条边的垂直平分线相交于一点
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
逆定理:到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
有垂直平分线,就有等腰三角形的产生
课堂小结
第2课时 线段垂直平分线的性质
A
C
E
B
D
下图表示的为某班的座位排列情况,每行每列的间隔相同.AB,C,D,E五位同学的作为如图所示,他们的座位存在怎么样的
关系?同学C、D、E与同学A、B之间的距离有什么特征?
情境引入
M
N
A
C
E
B
D
①直线MN是线段AB的垂直平分线
②猜测:直线MN上的点到A、B两点的距离相等
猜测1:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
C
合作探究
已知:如图,直线MN⊥线段AB,垂足为C, 且AC=CB.
求证:PA=PB
A
B
P
M
N
C
证明:∵ MN⊥AB 于点C (已知),
∴ ∠PCA= ∠PCB=90°(垂直的定义).
在 △PAC和△PBC中,
AC=BC(已知),
∠PCA= ∠PCB(已证),
PC=PC(公共边)
∴ △PAC ≌△ PBC(SAS).
∴PA=PB(全等三角形的对应边相等).
定理:线段垂直平分线上的点到这条线段两个
端点的距离相等。
A
B
P
M
N
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点和这条线段两个端点的距离相等
A
B
P
M
N
∵点P在线段AB的垂直平分线上(已知)
∴PA=PB
(线段垂直平分线上的点和这条线段
两个端点的距离相等。 )
猜测2:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
已知:如图,PA=PB
求证:P在AB的垂直平分线上
证明:过P点作MN⊥AB,垂足为C
∵PA=PB(已知)
∴AC=BC
(等腰三角形的“三线合一”)
A
B
P
M
N
C
∴ MN是AB的垂直平分线
∴P在AB的垂直平分线上
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
点P在线段AB的垂直平分线上
PA=PB
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
点P在线段AB的垂直平分线上
∵ PA=PB(已知)
∴点P在线段AB的垂直平分线上
(和一条线段两个端点
距离相等的点,在这条线段
的垂直平分线上)
A
B
P
M
N
例1 已知:如图,AB=AC=8cm ,DE是AB边的中垂线
交AC于点E,BC=6cm,求△BEC的周长
证明: ∵ DE是AB边的中垂线 (已知),
∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴AE+EC=BE+EC=8cm
(等式性质).
∵AC=8cm(已知),
∴ C△BEC=BE+EC+BC
=8+6=14cm
又∵ BC=6cm(已知)
有垂直平分线,就有等腰三角形的产生
例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
B
A
C
D
E
F
G
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
题型转换:证明三角形的三条边的垂直平分线相交于一点
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
逆定理:到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
有垂直平分线,就有等腰三角形的产生
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
