2021—2022学年北师大版数学九年级下册2.4实际问题与二次函数——抛物、拱桥问题课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.4实际问题与二次函数——抛物、拱桥问题课时对应练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 16:42:49 | ||
图片预览


文档简介
第12课时 实际问题与二次函数——抛物、拱桥问题
1.从地面竖直向上抛出一个小球,小球的上升高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=24t﹣4t2,那么,小球从抛出至回落到地面所需的时间是( )
A.6s B.4s C.3s D.2s
2.(2019 山西)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象﹣抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A.yx2 B.yx2
C.yx2 D.yx2
3.崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是__________米.
4.我国羽毛球球员林丹某次比赛中打出的羽毛球其运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系yx2x,则羽毛球飞出的水平距离为________米.
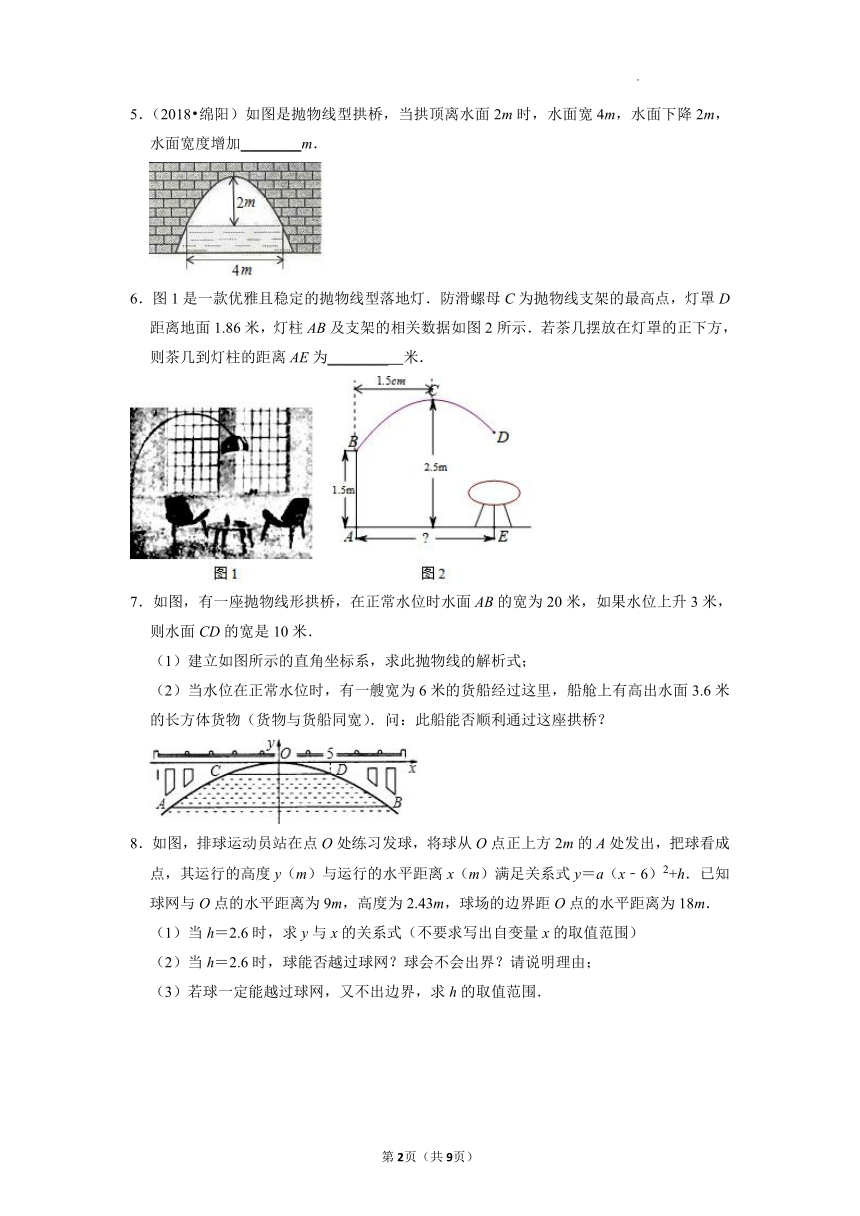
5.(2018 绵阳)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加________m.
6.图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________ 米.
7.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
8.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
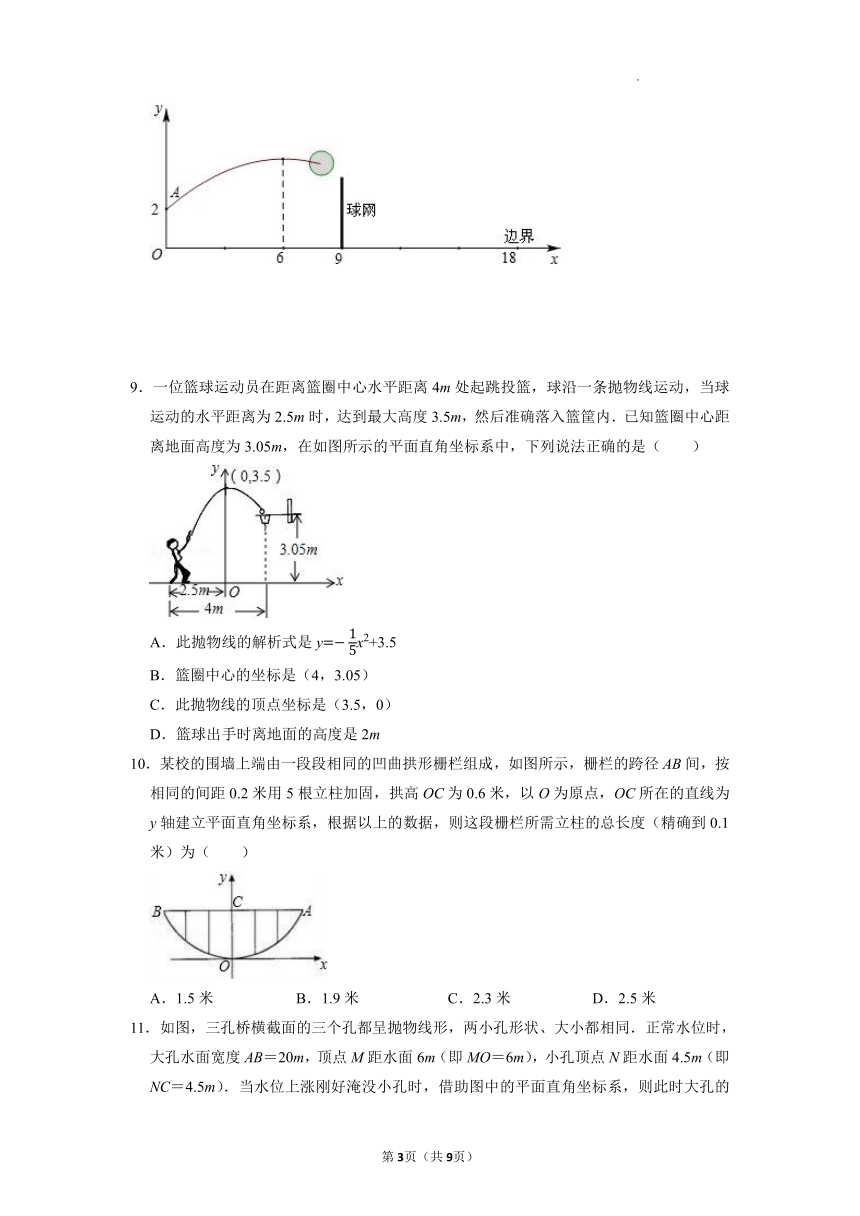
9.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是yx2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2m
10.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )
A.1.5米 B.1.9米 C.2.3米 D.2.5米
11.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20m,顶点M距水面6m(即MO=6m),小孔顶点N距水面4.5m(即NC=4.5m).当水位上涨刚好淹没小孔时,借助图中的平面直角坐标系,则此时大孔的水面宽度EF为________m.
12.如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为8m,两侧距地面4m高处各有一盏灯,两灯间的水平距离为6m,则这个门洞的高度为________m.(精确到0.1m)
13.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,以水平方向为x轴,建立平面直角坐标系,若选取A点为坐标原点时的抛物线的表达式为y,则选取点D为坐标原点时的抛物线表达式为 ________________ ,水管AB的长为________m.
14.某民房发生火灾.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和点F的离地高度分别相同,现消防员将水流抛物线向上平移5m,再向左后退________m,恰好把水喷到F处进行灭火.
15.如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD﹣DC﹣CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
16.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h(t﹣19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
【参考答案】
1.A.
2.B.
3.4.
4.5.
5.44.
6.2.7.
7.(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=102 a=100a,n+3=52a=25a,
即,
解得,
∴;
(2)∵货轮经过拱桥时的横坐标为x=3,
∴当x=3时,
∵(﹣4)>3.6
∴在正常水位时,此船能顺利通过这座拱桥.
答:在正常水位时,此船能顺利通过这座拱桥.
8.(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a,
故y与x的关系式为:y(x﹣6)2+2.6,
(2)当x=9时,y(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,,
解得:x1=6+218,x2=6﹣2(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时二次函数解析式为:y(x﹣6)2,
此时球若不出边界h,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时球要过网h,
故若球一定能越过球网,又不出边界,h的取值范围是:h.
解法二:y=a(x﹣6)2+h过点(0,2)点,代入解析式得:
2=36a+h,若球越过球网,则当x=9时,y>2.43,即9a+h>2.43解得h
球若不出边界,则当x=18时,y≤0,解得h.
故若球一定能越过球网,又不出边界,h的取值范围是:h.
9.A.
10.C.
11.10.
12.9.1.
13.y(x+2)2+3(﹣3≤x≤0);2.25.
14.5.提示:由图可知:A(0,21.2),B(0,9.2),C(0,6.2),D(0,1.2),
∵点B和点E、点C和点F的离地高度分别相同,
∴E(20,9.2),
设AE的直线解析式为y=kx+b,
,
∴,
∴yx+21.2,
∵A,E,F在同一直线上.
∴F(25,6.2),
设过D,E,F三点的抛物线为y=ax2+bx+c,
∴,
∴yx2x,
水流抛物线向上平移5m,设向左退了m米,
∴D(0,6.2),
设平移后的抛物线为y(x+m)2(x+m)+1.2+5,经过点F,
∴m=5或m=﹣25(舍),
∴向后退了5米.
15.(1)由题意可得:M(18,0),P(9,9).
(2)设抛物线解析式为:y=a(x﹣9)2+9
∵抛物线y=a(x﹣9)2+9经过点(0,0)
∴0=a(0﹣9)2+9,即a,
∴抛物线解析式为:y(x﹣9)2+9,即yx2+2x.
(3)设A(m,0),则B(18﹣m,0),C(18﹣m,m2+2m),D(m,m2+2m).
则“支撑架”总长AD+DC+CB=(m2+2m)+(18﹣2m)+(m2+2m)
m2+2m+18
(m﹣4.5)2+22.5.
∵此二次函数的图象开口向下.
∴当m=4.5米时,AD+DC+CB有最大值为22.5米.
16.(1)∵点C到ED的距离是11米,
∴OC=11,
设抛物线的解析式为y=ax2+11,由题意得B(8,8),
∴64a+11=8,
解得a,
∴yx2+11;
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至少为11﹣5=6(米),
∴6(t﹣19)2+8,
∴(t﹣19)2=256,
∴t﹣19=±16,
解得t1=35,t2=3,
∴35﹣3=32(小时).
答:需32小时禁止船只通行.
第9页(共9页)
1.从地面竖直向上抛出一个小球,小球的上升高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=24t﹣4t2,那么,小球从抛出至回落到地面所需的时间是( )
A.6s B.4s C.3s D.2s
2.(2019 山西)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象﹣抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A.yx2 B.yx2
C.yx2 D.yx2
3.崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是__________米.
4.我国羽毛球球员林丹某次比赛中打出的羽毛球其运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系yx2x,则羽毛球飞出的水平距离为________米.
5.(2018 绵阳)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加________m.
6.图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________ 米.
7.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
8.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
9.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是yx2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2m
10.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )
A.1.5米 B.1.9米 C.2.3米 D.2.5米
11.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20m,顶点M距水面6m(即MO=6m),小孔顶点N距水面4.5m(即NC=4.5m).当水位上涨刚好淹没小孔时,借助图中的平面直角坐标系,则此时大孔的水面宽度EF为________m.
12.如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为8m,两侧距地面4m高处各有一盏灯,两灯间的水平距离为6m,则这个门洞的高度为________m.(精确到0.1m)
13.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,以水平方向为x轴,建立平面直角坐标系,若选取A点为坐标原点时的抛物线的表达式为y,则选取点D为坐标原点时的抛物线表达式为 ________________ ,水管AB的长为________m.
14.某民房发生火灾.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和点F的离地高度分别相同,现消防员将水流抛物线向上平移5m,再向左后退________m,恰好把水喷到F处进行灭火.
15.如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD﹣DC﹣CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
16.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h(t﹣19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
【参考答案】
1.A.
2.B.
3.4.
4.5.
5.44.
6.2.7.
7.(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=102 a=100a,n+3=52a=25a,
即,
解得,
∴;
(2)∵货轮经过拱桥时的横坐标为x=3,
∴当x=3时,
∵(﹣4)>3.6
∴在正常水位时,此船能顺利通过这座拱桥.
答:在正常水位时,此船能顺利通过这座拱桥.
8.(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a,
故y与x的关系式为:y(x﹣6)2+2.6,
(2)当x=9时,y(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,,
解得:x1=6+218,x2=6﹣2(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时二次函数解析式为:y(x﹣6)2,
此时球若不出边界h,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时球要过网h,
故若球一定能越过球网,又不出边界,h的取值范围是:h.
解法二:y=a(x﹣6)2+h过点(0,2)点,代入解析式得:
2=36a+h,若球越过球网,则当x=9时,y>2.43,即9a+h>2.43解得h
球若不出边界,则当x=18时,y≤0,解得h.
故若球一定能越过球网,又不出边界,h的取值范围是:h.
9.A.
10.C.
11.10.
12.9.1.
13.y(x+2)2+3(﹣3≤x≤0);2.25.
14.5.提示:由图可知:A(0,21.2),B(0,9.2),C(0,6.2),D(0,1.2),
∵点B和点E、点C和点F的离地高度分别相同,
∴E(20,9.2),
设AE的直线解析式为y=kx+b,
,
∴,
∴yx+21.2,
∵A,E,F在同一直线上.
∴F(25,6.2),
设过D,E,F三点的抛物线为y=ax2+bx+c,
∴,
∴yx2x,
水流抛物线向上平移5m,设向左退了m米,
∴D(0,6.2),
设平移后的抛物线为y(x+m)2(x+m)+1.2+5,经过点F,
∴m=5或m=﹣25(舍),
∴向后退了5米.
15.(1)由题意可得:M(18,0),P(9,9).
(2)设抛物线解析式为:y=a(x﹣9)2+9
∵抛物线y=a(x﹣9)2+9经过点(0,0)
∴0=a(0﹣9)2+9,即a,
∴抛物线解析式为:y(x﹣9)2+9,即yx2+2x.
(3)设A(m,0),则B(18﹣m,0),C(18﹣m,m2+2m),D(m,m2+2m).
则“支撑架”总长AD+DC+CB=(m2+2m)+(18﹣2m)+(m2+2m)
m2+2m+18
(m﹣4.5)2+22.5.
∵此二次函数的图象开口向下.
∴当m=4.5米时,AD+DC+CB有最大值为22.5米.
16.(1)∵点C到ED的距离是11米,
∴OC=11,
设抛物线的解析式为y=ax2+11,由题意得B(8,8),
∴64a+11=8,
解得a,
∴yx2+11;
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至少为11﹣5=6(米),
∴6(t﹣19)2+8,
∴(t﹣19)2=256,
∴t﹣19=±16,
解得t1=35,t2=3,
∴35﹣3=32(小时).
答:需32小时禁止船只通行.
第9页(共9页)
