高二·上学期椭圆教学课件(复习课)
文档属性
| 名称 | 高二·上学期椭圆教学课件(复习课) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-29 15:49:17 | ||
图片预览











文档简介
课件43张PPT。 椭圆 星火教育大良校区数学组: 汤振国
一、椭圆的定义
平面内到两个定点F1,F2的距离之 等于常数
( )的点的集合叫作椭圆,这两个定点F1,F2
叫作椭圆的 ,两焦点F1,F2间的距离叫做椭圆的
.
大于|F1F2|焦点 焦距和在椭圆的定义中,若2a=|F1F2|或2a<|F1F2|动点P的轨迹如何??提示:当2a=|F1F2|时动点的轨迹是线段F1F2;当2a<|F1F2|时动点的轨迹是不存在的.?
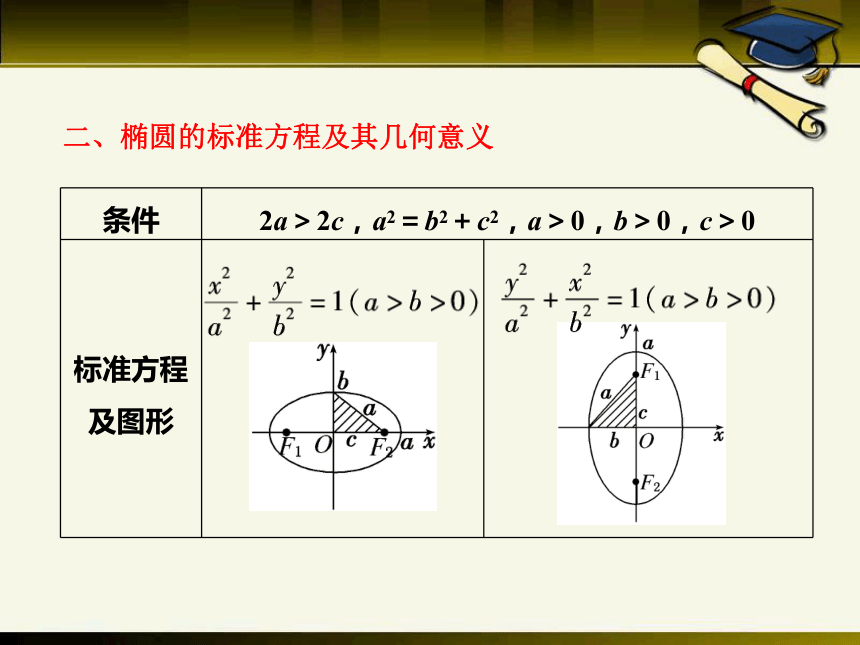
二、椭圆的标准方程及其几何意义
|x|≤a;|y|≤b
|x|≤b;|y|≤a
x轴y 轴、原点x轴、y轴、原点±a,0±b,0±c,00,±a0,±b0,±c2ca2-b2(0,1)
解析:分两种情况可得
1.若椭圆 的离心率为 ,则实数m ( )
或或
答案:A
2.设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|
+|PF2|=a(a>0),则动点P的轨迹是 ( )
A.椭圆 B.线段
C.椭圆或线段或不存在 D.不存在
解析:当a<6时,轨迹不存在;
当a=6时,轨迹为线段;
当a>6时,轨迹为椭圆.
答案:C
4.椭圆 的焦点坐标为________.解析:由方程知焦点在y轴上,故a2=9,b2=4,
∴c2=5,∴焦点为(0,± ).
答案:(0,± )
5.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实
数k的取值范围是________.
解析:椭圆方程化为 焦点在y轴上,则
即k<1.又k>0,∴0<k<1.
答案:(0,1)
3.已知椭圆 上一点P到椭圆一个焦点的距离为
3,则P到另一个焦点的距离为 ( )
A.2 B.3
C.5 D.7
解析:
答案:D
?
求椭圆的标准方程主要有定义法、待定系数法,有时还可根据条件用代入法.用特定系数法求椭圆方程的一般步骤是:
(1)作判断:根据条件判断椭圆的焦点在x轴上,还是在y
轴上,还是两个坐标轴都有可能.
(2)设方程:根据上述判断设方程 (a>b>0)
或 + =1(a>b>0).
(3)找关系:根据已知条件,建立关于a、b、c或m、n的
方程组.
(4)得方程:解方程组,将解代入所设方程,即为所求.
【注意】 当椭圆的焦点位置不明确而无法确定其标准方程时,可设 (m>0,n>0,m≠n),可以避免讨论和繁杂的计算,也可以设为Ax2+By2=1(A>0,B>0且A≠B),在已知椭圆上两点时,这种形式在解题时更简便.
已知点P在以坐标轴为对称轴的椭圆上,且P到两焦点的距离分别为5,3,过P且与长轴垂直的直线恰过椭圆的一个焦点,求椭圆的方程.
?利用定义可得2a,焦点位置不确定要注意讨论.【解】 设所求的椭圆方程为
=1(a>b>0),
由已知条件得解得 a=4,c=2,b2=12,
故所求方程为1.已知椭圆的中心在原点,以坐标轴为对称轴,且经过
两点 ,求椭圆的方程.
解:设椭圆的方程为mx2+ny2=1(m>0,n>0且m≠n).
∵椭圆经过P1、P2点,∴P1、P2点坐标适合椭圆方程,
则
两式联立,解得m=
∴所求椭圆方程为
1.椭圆性质的挖掘
(1)设椭圆 (a>b>0)上任意一点P(x,y),则当
x=0时,|OP|有最小值b,这时,P在短轴端点处;当
x=±a时,|OP|有最大值a,这时P在长轴端点处.
(2)椭圆上任意一点P(x,y)(y≠0)与两焦点F1(-c,0),F2(c,0)
构成的△PF1F2称为焦点三角形,其周长为2(a+c).
(3)椭圆的一个焦点、中心和短轴的一个端点构成直角三角
形,其中a是斜边,a2=b2+c2.
(4)过焦点F1的弦AB,则△ABF2的周长为4a.
2.离心率 在求法中要有整体求值思想或变形为 (2011·重庆高考)已知椭圆
a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0).若椭圆上存在点P使 则该椭圆的离心率的取值范围为________.
?
利用正弦定理得|PF1|、|PF2|的关系,结合定义可得PF2,再根据焦点弦长的最大最小值建立不等关系.?
【解析】 在△PF1F2中,由正弦定理知
①
又∵P在椭圆上,∴|PF1|+|PF2|=2a,将①代入得|PF2|=
∈(a-c,a+c),同除以a得,1-e< <1+e,【答案】 ( -1,1)
即|PF1|=e |PF2|.2.(2010·茂名一模)已知F1,F2是椭圆的两个焦点,过F1且
与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是等腰直角三有形,则这个椭圆的离心率是 ( )
解析:∵△ABF2是等腰直角三角形,∴|AF1|=|F1F2|,将x=-c代入椭圆方程 得A(-c,± ),从而 =2c,即a2-c2=2ac,整理得e2+2e-1=0,
解得e=-1± ,由e∈(0,1)得e= -1.
答案:C
3.(2010·枣庄一模)设椭圆 (m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的标准方程为________.
解析:抛物线y2=8x的焦点是(2,0),∴椭圆的半焦距c=2,
即m2-n2=4,又e= ∴m=4,
n2=12.
从而椭圆的方程为
答案:
1.直线方程与椭圆方程联立,消元后得到一元二次方程,
然后通过判别式Δ来判断直线和椭圆相交、相切或相离.
2.消元后得到的一元二次方程的根是直线和椭圆交点的横坐
标或纵坐标,通常是写成两根之和与两根之积的形式,这
是进一步解题的基础.
3.直线y=kx+b(k≠0)与圆锥曲线相交于A(x1,y1),B(x2,
y2)两点,则
|AB|=|x1-x2|=|y1-y2| (2010·厦门模拟)已知椭圆C的中心为坐标原点,一个长轴端点为(0,1),短轴端点和焦点所组成的四边形为正方形.若直线l与y轴交于点P(0,m),与椭圆C交于不同的两点A、B,且
(1)求椭圆C的方程;
(2)求实数m的取值范围.
?
(1)待定系数法易求.
(2)利用 建立k、m关系,根据Δ建立不等式可求m范围.
【解】 (1)依题意a=1,b=c,
∴b2= ,
∴所求椭圆C的方程为2x2+y2=1.
(2)设直线l:y=kx+m,消去y得
(k2+2)x2+2kmx+m2-1=0,
Δ=4k2m2-4(k2+2)(m2-1)
=-4(2m2-k2-2)>0,
∴2m2-k2-2<0,x1+x2=
∵ 设A(x1,y1),B(x2,y2),则
∴x1=-3x2,消去x1得 消去x2得
3k2m2=(k2+2)(1-m2),∴k2=
∴2m2-2- <0?(m2-1)(4m2-1)<0,
∴m∈
4.(2010·广州模拟)已知椭圆C: =1(a>b>0)的 离心率为 ,且经过P(1, ).
(1)求椭圆C的方程;
(2)设F是椭圆C的左焦点,判断以PF为直径的圆与以椭 圆长轴为直径的圆的位置关系,并说明理由.
解:(1)∵椭圆 (a>b>0)的离心率为 ,且
经过点P(1, ),
∴椭圆C的方程为
(2)∵a2=4,b2=3,∴c=
∴椭圆C的左焦点F的坐标为(-1,0).
以椭圆C的长轴为直径的圆的方程为x2+y2=4,圆心坐标是(0,0),半径为2.
以PF为直径的圆的方程为x2+ 圆心坐标是 ,半径为
∵两圆心之间的距离为 =2- , 故以PF为直径的圆与以椭圆长轴为直径的圆内切.
椭圆的定义、标准方程、几何性质一直是高考命题的热点,尤其是离心率问题是各地高考考查的重点,多在选择、填空中出现,主要考查学生结合定义,几何性质,分析问题解决问题的能力以及运算能力.2009年江苏综合考查了直线方程的求法、两直线的交点求法及离心率的求法.属中档题.(2009·江苏高考)如图,在平面直角坐标系xOy中,A1、A2、B1、B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为________.
?
[解析] A1(-a,0),B2(0,b).
故A1B2的方程为:
B1(0,-b),F(c,0).故B1F的方程为:
y= -b.
交点T的坐标满足:解之得T
∴OT中点 在椭圆 上.
故有整理得:3a2-10ac-c2=0.
∴e2+10e-3=0,∴e=2 - 5.
[答案] 2 -5
建立a、b、c的关系是解决离心率问题的关键,要充分利用图形及其性质.
平面内到两个定点F1,F2的距离之 等于常数
( )的点的集合叫作椭圆,这两个定点F1,F2
叫作椭圆的 ,两焦点F1,F2间的距离叫做椭圆的
.
大于|F1F2|焦点 焦距和在椭圆的定义中,若2a=|F1F2|或2a<|F1F2|动点P的轨迹如何??提示:当2a=|F1F2|时动点的轨迹是线段F1F2;当2a<|F1F2|时动点的轨迹是不存在的.?
二、椭圆的标准方程及其几何意义
|x|≤a;|y|≤b
|x|≤b;|y|≤a
x轴y 轴、原点x轴、y轴、原点±a,0±b,0±c,00,±a0,±b0,±c2ca2-b2(0,1)
解析:分两种情况可得
1.若椭圆 的离心率为 ,则实数m ( )
或或
答案:A
2.设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|
+|PF2|=a(a>0),则动点P的轨迹是 ( )
A.椭圆 B.线段
C.椭圆或线段或不存在 D.不存在
解析:当a<6时,轨迹不存在;
当a=6时,轨迹为线段;
当a>6时,轨迹为椭圆.
答案:C
4.椭圆 的焦点坐标为________.解析:由方程知焦点在y轴上,故a2=9,b2=4,
∴c2=5,∴焦点为(0,± ).
答案:(0,± )
5.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实
数k的取值范围是________.
解析:椭圆方程化为 焦点在y轴上,则
即k<1.又k>0,∴0<k<1.
答案:(0,1)
3.已知椭圆 上一点P到椭圆一个焦点的距离为
3,则P到另一个焦点的距离为 ( )
A.2 B.3
C.5 D.7
解析:
答案:D
?
求椭圆的标准方程主要有定义法、待定系数法,有时还可根据条件用代入法.用特定系数法求椭圆方程的一般步骤是:
(1)作判断:根据条件判断椭圆的焦点在x轴上,还是在y
轴上,还是两个坐标轴都有可能.
(2)设方程:根据上述判断设方程 (a>b>0)
或 + =1(a>b>0).
(3)找关系:根据已知条件,建立关于a、b、c或m、n的
方程组.
(4)得方程:解方程组,将解代入所设方程,即为所求.
【注意】 当椭圆的焦点位置不明确而无法确定其标准方程时,可设 (m>0,n>0,m≠n),可以避免讨论和繁杂的计算,也可以设为Ax2+By2=1(A>0,B>0且A≠B),在已知椭圆上两点时,这种形式在解题时更简便.
已知点P在以坐标轴为对称轴的椭圆上,且P到两焦点的距离分别为5,3,过P且与长轴垂直的直线恰过椭圆的一个焦点,求椭圆的方程.
?利用定义可得2a,焦点位置不确定要注意讨论.【解】 设所求的椭圆方程为
=1(a>b>0),
由已知条件得解得 a=4,c=2,b2=12,
故所求方程为1.已知椭圆的中心在原点,以坐标轴为对称轴,且经过
两点 ,求椭圆的方程.
解:设椭圆的方程为mx2+ny2=1(m>0,n>0且m≠n).
∵椭圆经过P1、P2点,∴P1、P2点坐标适合椭圆方程,
则
两式联立,解得m=
∴所求椭圆方程为
1.椭圆性质的挖掘
(1)设椭圆 (a>b>0)上任意一点P(x,y),则当
x=0时,|OP|有最小值b,这时,P在短轴端点处;当
x=±a时,|OP|有最大值a,这时P在长轴端点处.
(2)椭圆上任意一点P(x,y)(y≠0)与两焦点F1(-c,0),F2(c,0)
构成的△PF1F2称为焦点三角形,其周长为2(a+c).
(3)椭圆的一个焦点、中心和短轴的一个端点构成直角三角
形,其中a是斜边,a2=b2+c2.
(4)过焦点F1的弦AB,则△ABF2的周长为4a.
2.离心率 在求法中要有整体求值思想或变形为 (2011·重庆高考)已知椭圆
a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0).若椭圆上存在点P使 则该椭圆的离心率的取值范围为________.
?
利用正弦定理得|PF1|、|PF2|的关系,结合定义可得PF2,再根据焦点弦长的最大最小值建立不等关系.?
【解析】 在△PF1F2中,由正弦定理知
①
又∵P在椭圆上,∴|PF1|+|PF2|=2a,将①代入得|PF2|=
∈(a-c,a+c),同除以a得,1-e< <1+e,【答案】 ( -1,1)
即|PF1|=e |PF2|.2.(2010·茂名一模)已知F1,F2是椭圆的两个焦点,过F1且
与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是等腰直角三有形,则这个椭圆的离心率是 ( )
解析:∵△ABF2是等腰直角三角形,∴|AF1|=|F1F2|,将x=-c代入椭圆方程 得A(-c,± ),从而 =2c,即a2-c2=2ac,整理得e2+2e-1=0,
解得e=-1± ,由e∈(0,1)得e= -1.
答案:C
3.(2010·枣庄一模)设椭圆 (m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的标准方程为________.
解析:抛物线y2=8x的焦点是(2,0),∴椭圆的半焦距c=2,
即m2-n2=4,又e= ∴m=4,
n2=12.
从而椭圆的方程为
答案:
1.直线方程与椭圆方程联立,消元后得到一元二次方程,
然后通过判别式Δ来判断直线和椭圆相交、相切或相离.
2.消元后得到的一元二次方程的根是直线和椭圆交点的横坐
标或纵坐标,通常是写成两根之和与两根之积的形式,这
是进一步解题的基础.
3.直线y=kx+b(k≠0)与圆锥曲线相交于A(x1,y1),B(x2,
y2)两点,则
|AB|=|x1-x2|=|y1-y2| (2010·厦门模拟)已知椭圆C的中心为坐标原点,一个长轴端点为(0,1),短轴端点和焦点所组成的四边形为正方形.若直线l与y轴交于点P(0,m),与椭圆C交于不同的两点A、B,且
(1)求椭圆C的方程;
(2)求实数m的取值范围.
?
(1)待定系数法易求.
(2)利用 建立k、m关系,根据Δ建立不等式可求m范围.
【解】 (1)依题意a=1,b=c,
∴b2= ,
∴所求椭圆C的方程为2x2+y2=1.
(2)设直线l:y=kx+m,消去y得
(k2+2)x2+2kmx+m2-1=0,
Δ=4k2m2-4(k2+2)(m2-1)
=-4(2m2-k2-2)>0,
∴2m2-k2-2<0,x1+x2=
∵ 设A(x1,y1),B(x2,y2),则
∴x1=-3x2,消去x1得 消去x2得
3k2m2=(k2+2)(1-m2),∴k2=
∴2m2-2- <0?(m2-1)(4m2-1)<0,
∴m∈
4.(2010·广州模拟)已知椭圆C: =1(a>b>0)的 离心率为 ,且经过P(1, ).
(1)求椭圆C的方程;
(2)设F是椭圆C的左焦点,判断以PF为直径的圆与以椭 圆长轴为直径的圆的位置关系,并说明理由.
解:(1)∵椭圆 (a>b>0)的离心率为 ,且
经过点P(1, ),
∴椭圆C的方程为
(2)∵a2=4,b2=3,∴c=
∴椭圆C的左焦点F的坐标为(-1,0).
以椭圆C的长轴为直径的圆的方程为x2+y2=4,圆心坐标是(0,0),半径为2.
以PF为直径的圆的方程为x2+ 圆心坐标是 ,半径为
∵两圆心之间的距离为 =2- , 故以PF为直径的圆与以椭圆长轴为直径的圆内切.
椭圆的定义、标准方程、几何性质一直是高考命题的热点,尤其是离心率问题是各地高考考查的重点,多在选择、填空中出现,主要考查学生结合定义,几何性质,分析问题解决问题的能力以及运算能力.2009年江苏综合考查了直线方程的求法、两直线的交点求法及离心率的求法.属中档题.(2009·江苏高考)如图,在平面直角坐标系xOy中,A1、A2、B1、B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为________.
?
[解析] A1(-a,0),B2(0,b).
故A1B2的方程为:
B1(0,-b),F(c,0).故B1F的方程为:
y= -b.
交点T的坐标满足:解之得T
∴OT中点 在椭圆 上.
故有整理得:3a2-10ac-c2=0.
∴e2+10e-3=0,∴e=2 - 5.
[答案] 2 -5
建立a、b、c的关系是解决离心率问题的关键,要充分利用图形及其性质.
