2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(3)课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(3)课时对应练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 117.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 17:17:23 | ||
图片预览



文档简介
第05课时 二次函数y=a(x-h)2 +k的函数图像和性质(3)
1.将抛物线y=﹣2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )
A.y=﹣2(x+1)2 B.y=﹣2(x+1)2+2
C.y=﹣2(x﹣1)2+2 D.y=﹣2(x﹣1)2+1
2.对于抛物线y(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1;
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小;
⑤抛物线与y轴的交点坐标为(0,3).
其中正确的有( )个.
A.1 B.2 C.3 D.4
3.如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的h,k,m,n都是常数,则下列关系不正确的是( )
A.h<0,k>0 B.m<0,n>0 C.h=m D.k=n
4.对于二次函数y=a(x﹣h)2+k,对称轴是_______,顶点坐标是_______.
(1)当a>0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y随x的增大而_______,当x=_______时,y有最_______值,是_______;
(2)当a<0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y随x的增大而_______,当x=时,y有最_______值,是_______.
5.如图,把抛物线yx2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线yx2交于点Q,则图中阴影部分的面积为_______.
6.对于函数y=﹣2(x﹣1)2,当x≤a时,y随x的增大而增大,则a的范围为_______.
7.抛物线的顶点为C,已知y=﹣kx+3的图象经过点C,则这个一次函数图象与两坐标轴所围成的三角形面积为_______.
8.已知二次函数y=(x﹣2a)2+(a﹣1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”,如图分别是当a=﹣1,a=0,a=l,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 _______.
9.已知在平面直角坐标系中,抛物线l1的解析式为y=﹣x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(3,﹣1),且对称轴为x=1.
(1)求抛物线l2的解析式;
(2)求抛物线l2的顶点坐标;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点坐标为B,直线OB于抛物线l3的另一个交点为C,当OB=OC时,求C点坐标.
10.已知二次函数y=(x﹣1)2﹣4的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,顶点为D.
(1)求点A,B,C,D的坐标.并画出该二次函数的大致图象;
(2)说出抛物线y=(x﹣1)2﹣4可由抛物线y=x2如何平移得到;
(3)求四边形BOCD的面积.
11.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
12.已知yx2的图象是抛物线,若抛物线不动,把x轴,y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )
A.y(x﹣2)2+2 B.y(x+2)2﹣2
C.y(x﹣2)2﹣2 D.y(x+2)2+2
13.已知抛物线C:y(x﹣1)2﹣1,顶点为D,将C沿水平方向向右(或向左)平移m个单位,得到抛物线C1,顶点为D1,C与C1相交于点Q,若∠DQD1=60°,则m等于( )
A.±4 B.±2 C.﹣2或2 D.﹣4或4
14.当0≤x≤3时,直线y=a与抛物线y=(x﹣1)2﹣3有交点,则a的取值范围是_______ .
15.已知函数y,点P(a,ka)在该函数上,若这样的点P恰好有三个,则k的值为_______.
16.已知函数y使y=a成立的x的值恰好只有3个时,a的值为______.
17.如图,在平面直角坐标系中,点A、B的坐标分别为(16,0),(0,3),连结AB,P是线段AO上一动点(不与点A、O重合).过A、P两点的抛物线和过P、O两点的抛物线的开口均向下,它们的顶点E、F均在线段AB上.设这两个二次函数的最大值的差为S,则S=_______.
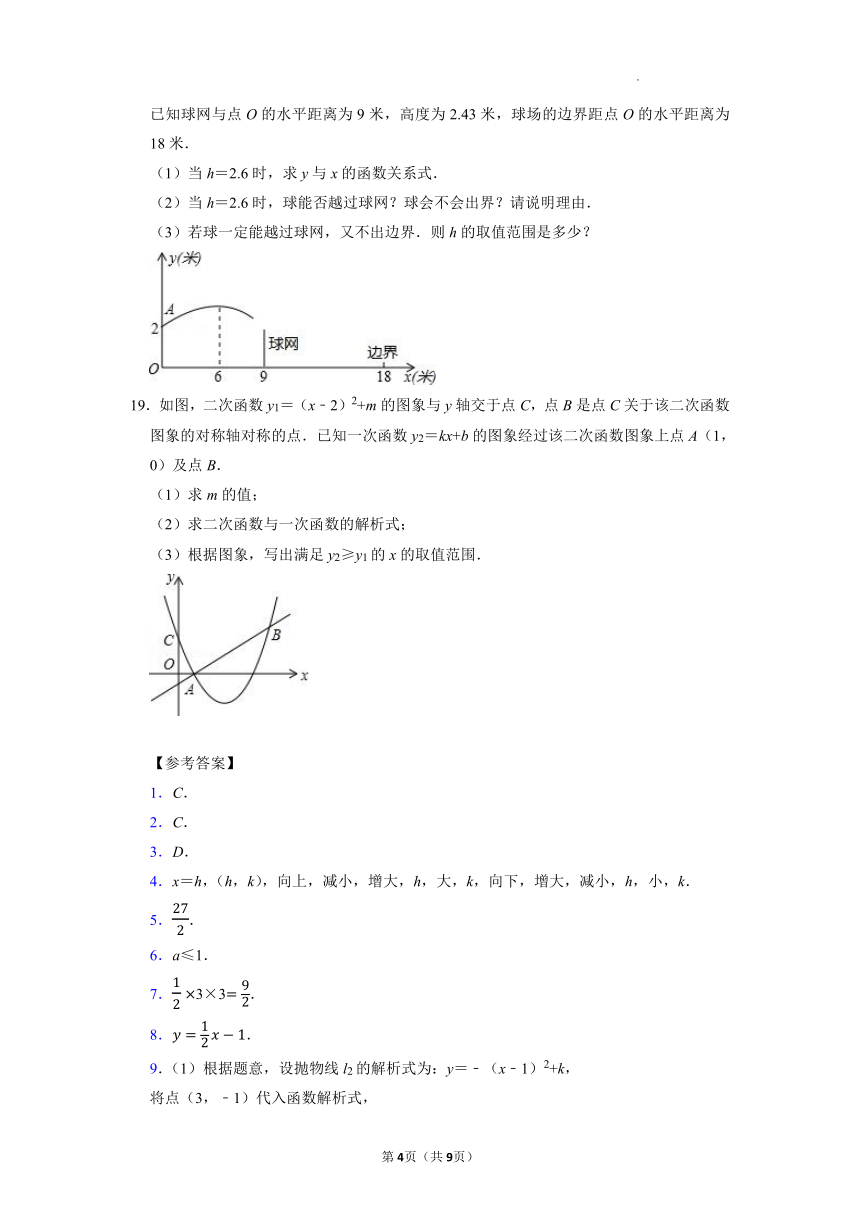
18.如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?
19.如图,二次函数y1=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y2=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求m的值;
(2)求二次函数与一次函数的解析式;
(3)根据图象,写出满足y2≥y1的x的取值范围.
【参考答案】
1.C.
2.C.
3.D.
4.x=h,(h,k),向上,减小,增大,h,大,k,向下,增大,减小,h,小,k.
5..
6.a≤1.
7.3×3.
8..
9.(1)根据题意,设抛物线l2的解析式为:y=﹣(x﹣1)2+k,
将点(3,﹣1)代入函数解析式,
∴﹣1=﹣4+k,
解得:k=3,
∴抛物线l2的解析式为:y=﹣(x﹣1)2+3;
(2)∴抛物线l2的顶点坐标为(1,3);
(3)设l3的解析式为:y=﹣(x﹣1)2+3+m,
∴B点坐标为(1,3+m),
∵B,O,C三点共线且OB=OC,
∴C点坐标为(﹣1,﹣3﹣m),
∵C在l3上,
∴﹣(﹣1﹣1)2+3+m=﹣3﹣m,
∴m=﹣1,
∴C点坐标为(﹣1,﹣2).
10.(1)令y=0,(x﹣1)2﹣4=0,解得x=3或﹣1,得A(﹣1,0),B(3,0),
令x=0,y=﹣3,得C(0,﹣3),顶点D(1,﹣4).
图象如图所示,
(2)把抛物线y=x2抛向右平移1个单位,再向下平移4个单位得到抛物线y=(x﹣1)2﹣4.
(3)连接OD,S四边形CDBO=S△OCD+S△OBD 3 1 3 4.
11.A.
12.B.
13.A.提示:抛物线CC:y(x﹣1)2﹣1沿水平方向向右(或向左)平移m个单位得到y(x﹣m﹣1)2﹣1,
∴D(1,﹣1),D1(m+1,﹣1),
∴Q点的横坐标为:,
代入y(x﹣1)2﹣1求得Q(,1),
若∠DQD1=60°,则△DQD1是等边三角形,
∴QD=DD1=|m|,
由勾股定理得,(1)2+(1+1)2=m2,
解得m=±4。
14.﹣3≤a≤1。提示:
∵抛物线的顶点为(1,﹣3),而0≤x≤3
∴抛物线y的取值为﹣3≤y≤1
∵y=a,则直线y与x轴平行,
∴要使直线y=a与抛物线y=(x﹣1)2﹣3有交点,
∴抛物线y的取值为﹣3≤y≤1,即为a的取值范围,
∴﹣3≤a≤1。
15.2或14.提示:
作出函数图象如上图所示,
∵点P(a,ka)在该函数上,
∴点P(a,ka)在y=kx上,
①当x=4,代入函数y=(x﹣7)2﹣1得y=8,可得:k=2,
②由 得
kx=(x﹣7)2﹣1
化简得:x2﹣(14+k)x+48=0
∴令△=(14+k)2﹣192=0
解得:k14或k14(舍去)
16.2.提示:函数y的图象如图:
根据图象知道当y=2时,对应成立的x值恰好有三个,
∴a=2.
17..提示:∵点A、B的坐标分别为(16,0),(0,3),
∴设直线AB解析式为y=kx
∴0=16k
∴k
∴yx
设P点坐标为(m,0),则AP=16﹣m
∴E点横坐标为,F点横坐标为:m8
∴这两个二次函数的最大值的差
S[(8)]
。
18.(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a,
故y与x的关系式为:y(x﹣6)2+2.6,
(2)当x=9时,y(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,(x﹣6)2+2.6=0,
解得:x1=618,x2=6(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得,
此时二次函数解析式为:y(x﹣6)2,
此时球若不出边界h,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:,
解得,
此时球要过网h,
故若球一定能越过球网,又不出边界,h的取值范围是:h.
解法二:y=a(x﹣6)2+h过点(0,2)点,代入解析式得:
2=36a+h,若球越过球网,则当x=9时,y>2.43,即9a+h>2.43解得h
球若不出边界,则当x=18时,y≤0,解得h.
故若球一定能越过球网,又不出边界,h的取值范围是:h.
19.(1)将点A(1,0)代入y=(x﹣2)2+m得,
(1﹣2)2+m=0,1+m=0,m=﹣1;
(2)二次函数解析式为y=(x﹣2)2﹣1,
当x=0时,y=4﹣1=3,故C点坐标为(0,3),
由于C和B关于对称轴对称,在设B点坐标为(x,3),
令y=3,有(x﹣2)2﹣1=3,
解得x=4或x=0,
则B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得,,
解得,
所以,一次函数解析式为y=x﹣1;
(3)∵A、B坐标为(1,0),(4,3),
∴当y2≥y1时,1≤x≤4.
第10页(共10页)
1.将抛物线y=﹣2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )
A.y=﹣2(x+1)2 B.y=﹣2(x+1)2+2
C.y=﹣2(x﹣1)2+2 D.y=﹣2(x﹣1)2+1
2.对于抛物线y(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1;
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小;
⑤抛物线与y轴的交点坐标为(0,3).
其中正确的有( )个.
A.1 B.2 C.3 D.4
3.如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的h,k,m,n都是常数,则下列关系不正确的是( )
A.h<0,k>0 B.m<0,n>0 C.h=m D.k=n
4.对于二次函数y=a(x﹣h)2+k,对称轴是_______,顶点坐标是_______.
(1)当a>0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y随x的增大而_______,当x=_______时,y有最_______值,是_______;
(2)当a<0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y随x的增大而_______,当x=时,y有最_______值,是_______.
5.如图,把抛物线yx2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线yx2交于点Q,则图中阴影部分的面积为_______.
6.对于函数y=﹣2(x﹣1)2,当x≤a时,y随x的增大而增大,则a的范围为_______.
7.抛物线的顶点为C,已知y=﹣kx+3的图象经过点C,则这个一次函数图象与两坐标轴所围成的三角形面积为_______.
8.已知二次函数y=(x﹣2a)2+(a﹣1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”,如图分别是当a=﹣1,a=0,a=l,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 _______.
9.已知在平面直角坐标系中,抛物线l1的解析式为y=﹣x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(3,﹣1),且对称轴为x=1.
(1)求抛物线l2的解析式;
(2)求抛物线l2的顶点坐标;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点坐标为B,直线OB于抛物线l3的另一个交点为C,当OB=OC时,求C点坐标.
10.已知二次函数y=(x﹣1)2﹣4的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,顶点为D.
(1)求点A,B,C,D的坐标.并画出该二次函数的大致图象;
(2)说出抛物线y=(x﹣1)2﹣4可由抛物线y=x2如何平移得到;
(3)求四边形BOCD的面积.
11.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
12.已知yx2的图象是抛物线,若抛物线不动,把x轴,y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )
A.y(x﹣2)2+2 B.y(x+2)2﹣2
C.y(x﹣2)2﹣2 D.y(x+2)2+2
13.已知抛物线C:y(x﹣1)2﹣1,顶点为D,将C沿水平方向向右(或向左)平移m个单位,得到抛物线C1,顶点为D1,C与C1相交于点Q,若∠DQD1=60°,则m等于( )
A.±4 B.±2 C.﹣2或2 D.﹣4或4
14.当0≤x≤3时,直线y=a与抛物线y=(x﹣1)2﹣3有交点,则a的取值范围是_______ .
15.已知函数y,点P(a,ka)在该函数上,若这样的点P恰好有三个,则k的值为_______.
16.已知函数y使y=a成立的x的值恰好只有3个时,a的值为______.
17.如图,在平面直角坐标系中,点A、B的坐标分别为(16,0),(0,3),连结AB,P是线段AO上一动点(不与点A、O重合).过A、P两点的抛物线和过P、O两点的抛物线的开口均向下,它们的顶点E、F均在线段AB上.设这两个二次函数的最大值的差为S,则S=_______.
18.如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?
19.如图,二次函数y1=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y2=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求m的值;
(2)求二次函数与一次函数的解析式;
(3)根据图象,写出满足y2≥y1的x的取值范围.
【参考答案】
1.C.
2.C.
3.D.
4.x=h,(h,k),向上,减小,增大,h,大,k,向下,增大,减小,h,小,k.
5..
6.a≤1.
7.3×3.
8..
9.(1)根据题意,设抛物线l2的解析式为:y=﹣(x﹣1)2+k,
将点(3,﹣1)代入函数解析式,
∴﹣1=﹣4+k,
解得:k=3,
∴抛物线l2的解析式为:y=﹣(x﹣1)2+3;
(2)∴抛物线l2的顶点坐标为(1,3);
(3)设l3的解析式为:y=﹣(x﹣1)2+3+m,
∴B点坐标为(1,3+m),
∵B,O,C三点共线且OB=OC,
∴C点坐标为(﹣1,﹣3﹣m),
∵C在l3上,
∴﹣(﹣1﹣1)2+3+m=﹣3﹣m,
∴m=﹣1,
∴C点坐标为(﹣1,﹣2).
10.(1)令y=0,(x﹣1)2﹣4=0,解得x=3或﹣1,得A(﹣1,0),B(3,0),
令x=0,y=﹣3,得C(0,﹣3),顶点D(1,﹣4).
图象如图所示,
(2)把抛物线y=x2抛向右平移1个单位,再向下平移4个单位得到抛物线y=(x﹣1)2﹣4.
(3)连接OD,S四边形CDBO=S△OCD+S△OBD 3 1 3 4.
11.A.
12.B.
13.A.提示:抛物线CC:y(x﹣1)2﹣1沿水平方向向右(或向左)平移m个单位得到y(x﹣m﹣1)2﹣1,
∴D(1,﹣1),D1(m+1,﹣1),
∴Q点的横坐标为:,
代入y(x﹣1)2﹣1求得Q(,1),
若∠DQD1=60°,则△DQD1是等边三角形,
∴QD=DD1=|m|,
由勾股定理得,(1)2+(1+1)2=m2,
解得m=±4。
14.﹣3≤a≤1。提示:
∵抛物线的顶点为(1,﹣3),而0≤x≤3
∴抛物线y的取值为﹣3≤y≤1
∵y=a,则直线y与x轴平行,
∴要使直线y=a与抛物线y=(x﹣1)2﹣3有交点,
∴抛物线y的取值为﹣3≤y≤1,即为a的取值范围,
∴﹣3≤a≤1。
15.2或14.提示:
作出函数图象如上图所示,
∵点P(a,ka)在该函数上,
∴点P(a,ka)在y=kx上,
①当x=4,代入函数y=(x﹣7)2﹣1得y=8,可得:k=2,
②由 得
kx=(x﹣7)2﹣1
化简得:x2﹣(14+k)x+48=0
∴令△=(14+k)2﹣192=0
解得:k14或k14(舍去)
16.2.提示:函数y的图象如图:
根据图象知道当y=2时,对应成立的x值恰好有三个,
∴a=2.
17..提示:∵点A、B的坐标分别为(16,0),(0,3),
∴设直线AB解析式为y=kx
∴0=16k
∴k
∴yx
设P点坐标为(m,0),则AP=16﹣m
∴E点横坐标为,F点横坐标为:m8
∴这两个二次函数的最大值的差
S[(8)]
。
18.(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a,
故y与x的关系式为:y(x﹣6)2+2.6,
(2)当x=9时,y(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,(x﹣6)2+2.6=0,
解得:x1=618,x2=6(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得,
此时二次函数解析式为:y(x﹣6)2,
此时球若不出边界h,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:,
解得,
此时球要过网h,
故若球一定能越过球网,又不出边界,h的取值范围是:h.
解法二:y=a(x﹣6)2+h过点(0,2)点,代入解析式得:
2=36a+h,若球越过球网,则当x=9时,y>2.43,即9a+h>2.43解得h
球若不出边界,则当x=18时,y≤0,解得h.
故若球一定能越过球网,又不出边界,h的取值范围是:h.
19.(1)将点A(1,0)代入y=(x﹣2)2+m得,
(1﹣2)2+m=0,1+m=0,m=﹣1;
(2)二次函数解析式为y=(x﹣2)2﹣1,
当x=0时,y=4﹣1=3,故C点坐标为(0,3),
由于C和B关于对称轴对称,在设B点坐标为(x,3),
令y=3,有(x﹣2)2﹣1=3,
解得x=4或x=0,
则B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得,,
解得,
所以,一次函数解析式为y=x﹣1;
(3)∵A、B坐标为(1,0),(4,3),
∴当y2≥y1时,1≤x≤4.
第10页(共10页)
