2021—2022学年北师大版数学九年级下册2.2二次函数y=ax2+bx+c的图象和性质(2)课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.2二次函数y=ax2+bx+c的图象和性质(2)课时对应练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 171.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览

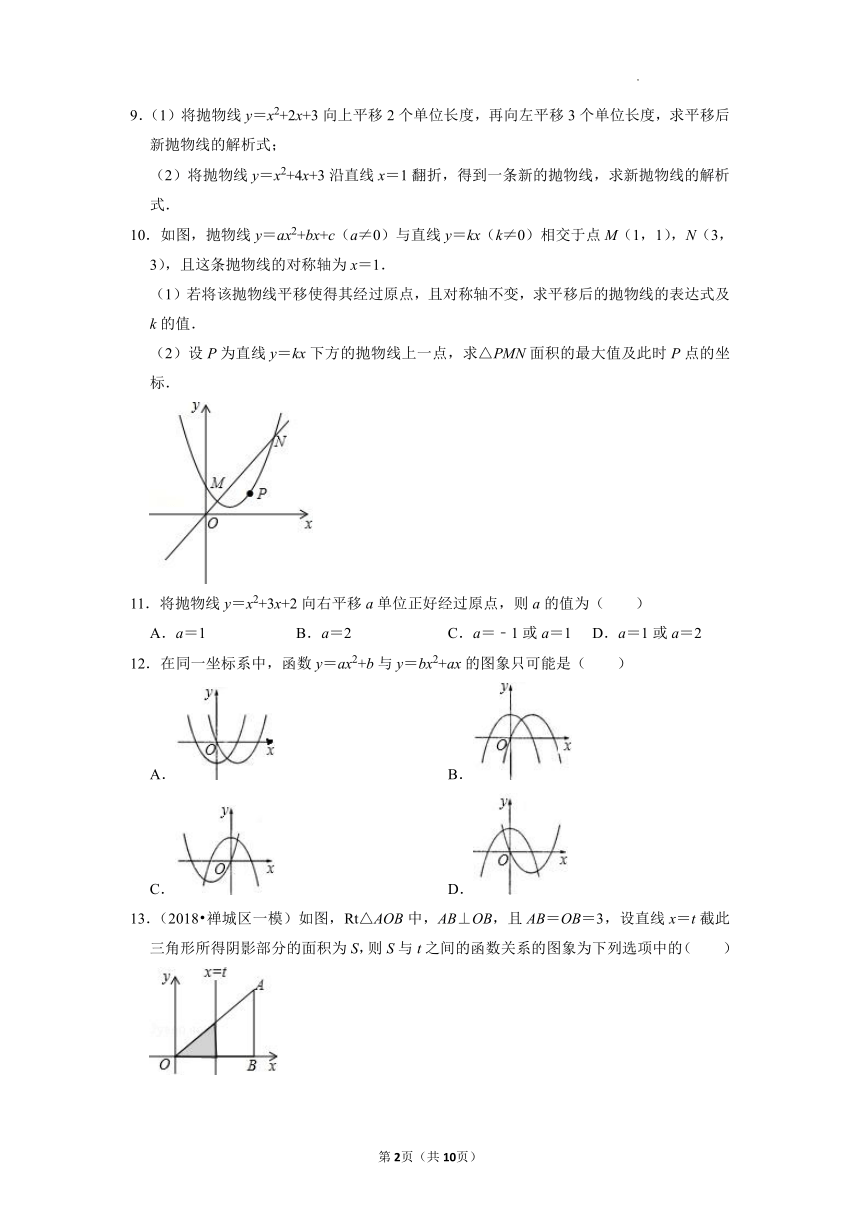
文档简介
第07课时 二次函数y=ax2+bx+c的图象和性质(2)——图象性质及平移
1.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 …
y … ﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …
则该函数图象的对称轴是( )
A.直线x=﹣3 B.直线x=﹣2 C.直线x=﹣1 D.直线x=0
2.若点(﹣3,y1)、(1,y2)、(3,y3)都在二次函数y=(x+1)2+k的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1=y3>y2 C.y1=y2<y3 D.y1=y2>y3
3.抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )
A.b=2,c=﹣6 B.b=2,c=0 C.b=﹣6,c=8 D.b=﹣6,c=2
7.已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x ﹣3 0 3
y 0 3 3
则函数y=ax+bc不经过的象限是第_______象限.
5.若二次函数y=(a﹣1)x2+3x+a2﹣1的图象经过原点,则a的值必为_____.
6.将抛物线y=3x2﹣6x+5绕顶点旋转180°,再沿对称轴平移,得到一条与直线y=﹣x﹣2交于点(2,m)的新抛物线,新抛物线的解析式为__________ .
7.当x=a与x=b(a≠b)时,代数式x2﹣2x+3的值相等,则x=a+b时,代数式x2﹣2x+3的值为_____.
8.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
9.(1)将抛物线y=x2+2x+3向上平移2个单位长度,再向左平移3个单位长度,求平移后新抛物线的解析式;
(2)将抛物线y=x2+4x+3沿直线x=1翻折,得到一条新的抛物线,求新抛物线的解析式.
10.如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的表达式及k的值.
(2)设P为直线y=kx下方的抛物线上一点,求△PMN面积的最大值及此时P点的坐标.
11.将抛物线y=x2+3x+2向右平移a单位正好经过原点,则a的值为( )
A.a=1 B.a=2 C.a=﹣1或a=1 D.a=1或a=2
12.在同一坐标系中,函数y=ax2+b与y=bx2+ax的图象只可能是( )
A. B.
C. D.
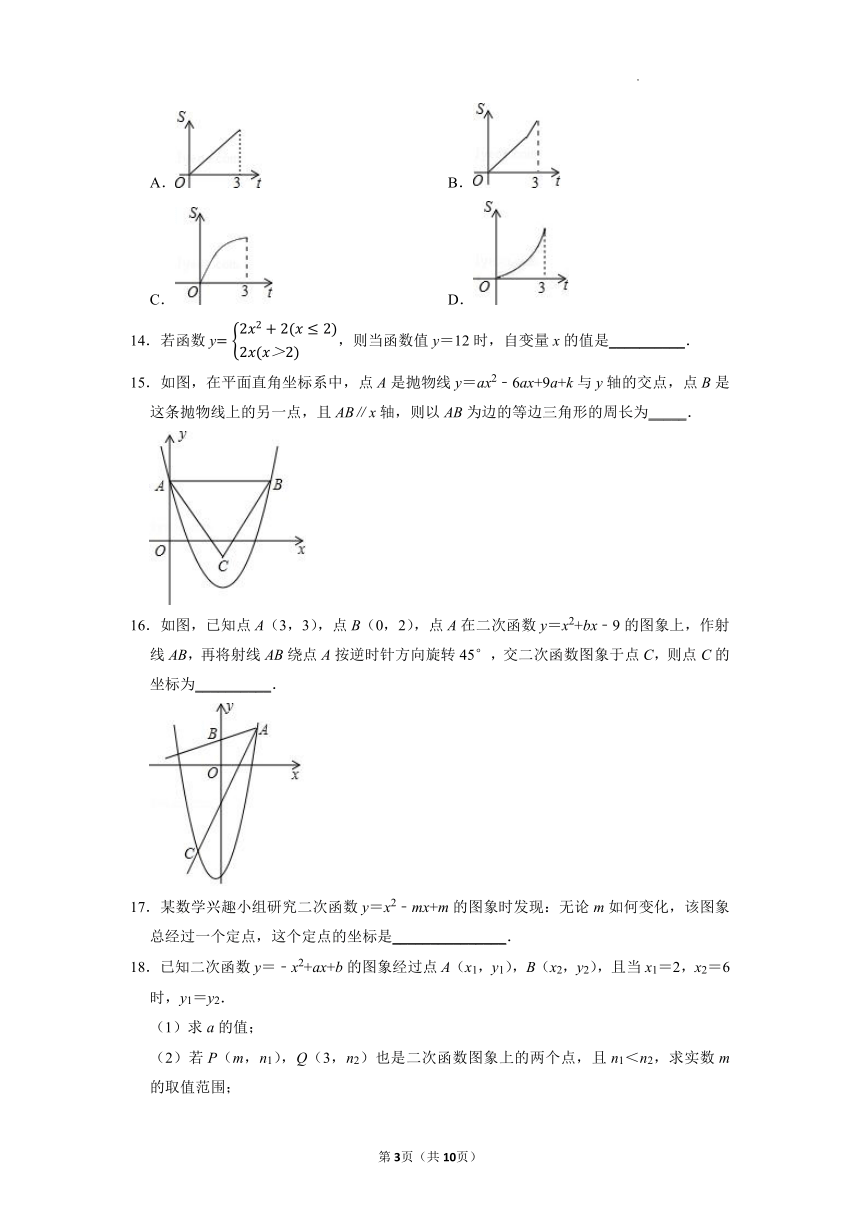
13.(2018 禅城区一模)如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
14.若函数y,则当函数值y=12时,自变量x的值是__________.
15.如图,在平面直角坐标系中,点A是抛物线y=ax2﹣6ax+9a+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形的周长为_____.
16.如图,已知点A(3,3),点B(0,2),点A在二次函数y=x2+bx﹣9的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交二次函数图象于点C,则点C的坐标为__________.
17.某数学兴趣小组研究二次函数y=x2﹣mx+m的图象时发现:无论m如何变化,该图象总经过一个定点,这个定点的坐标是_______________.
18.已知二次函数y=﹣x2+ax+b的图象经过点A(x1,y1),B(x2,y2),且当x1=2,x2=6时,y1=y2.
(1)求a的值;
(2)若P(m,n1),Q(3,n2)也是二次函数图象上的两个点,且n1<n2,求实数m的取值范围;
(3)若T(t,2t)不在抛物线上,求b的取值范围.
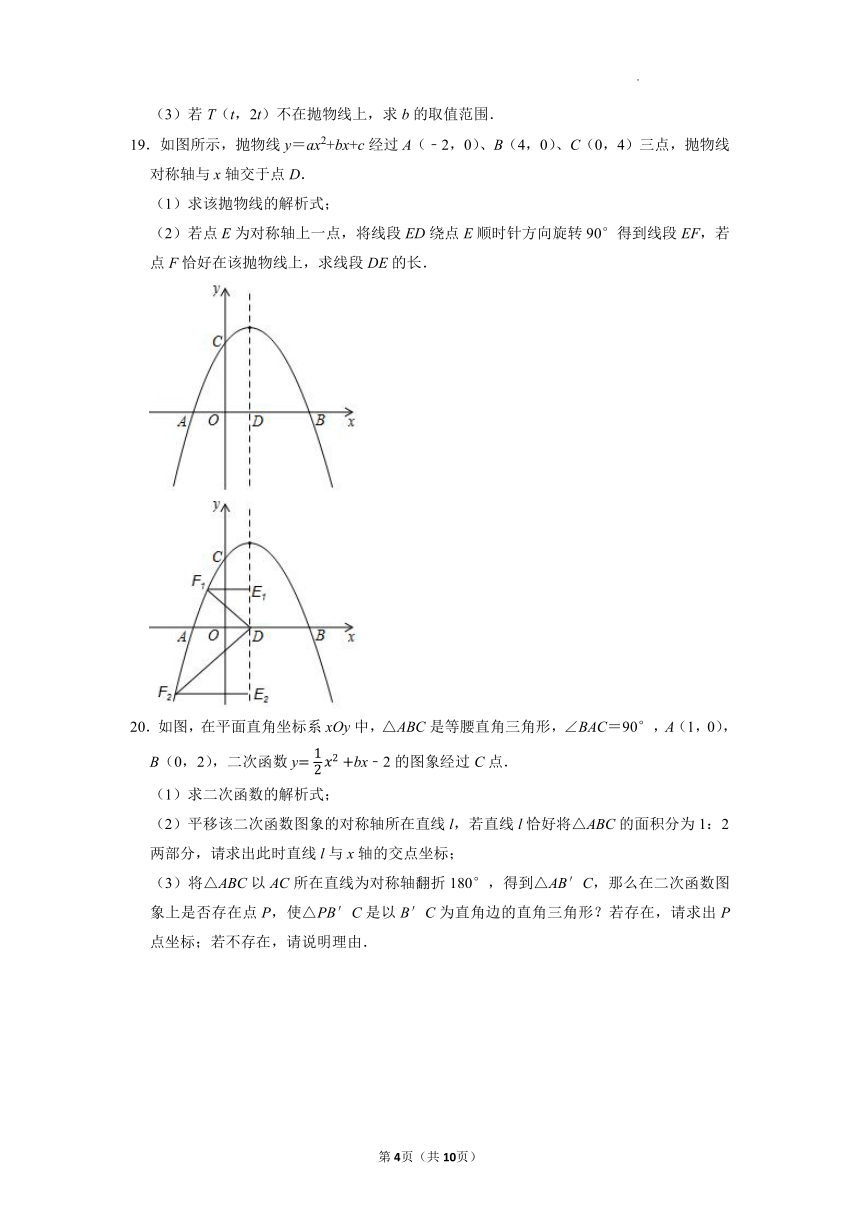
19.如图所示,抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)、C(0,4)三点,抛物线对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E为对称轴上一点,将线段ED绕点E顺时针方向旋转90°得到线段EF,若点F恰好在该抛物线上,求线段DE的长.
20.如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数ybx﹣2的图象经过C点.
(1)求二次函数的解析式;
(2)平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;
(3)将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P点坐标;若不存在,请说明理由.
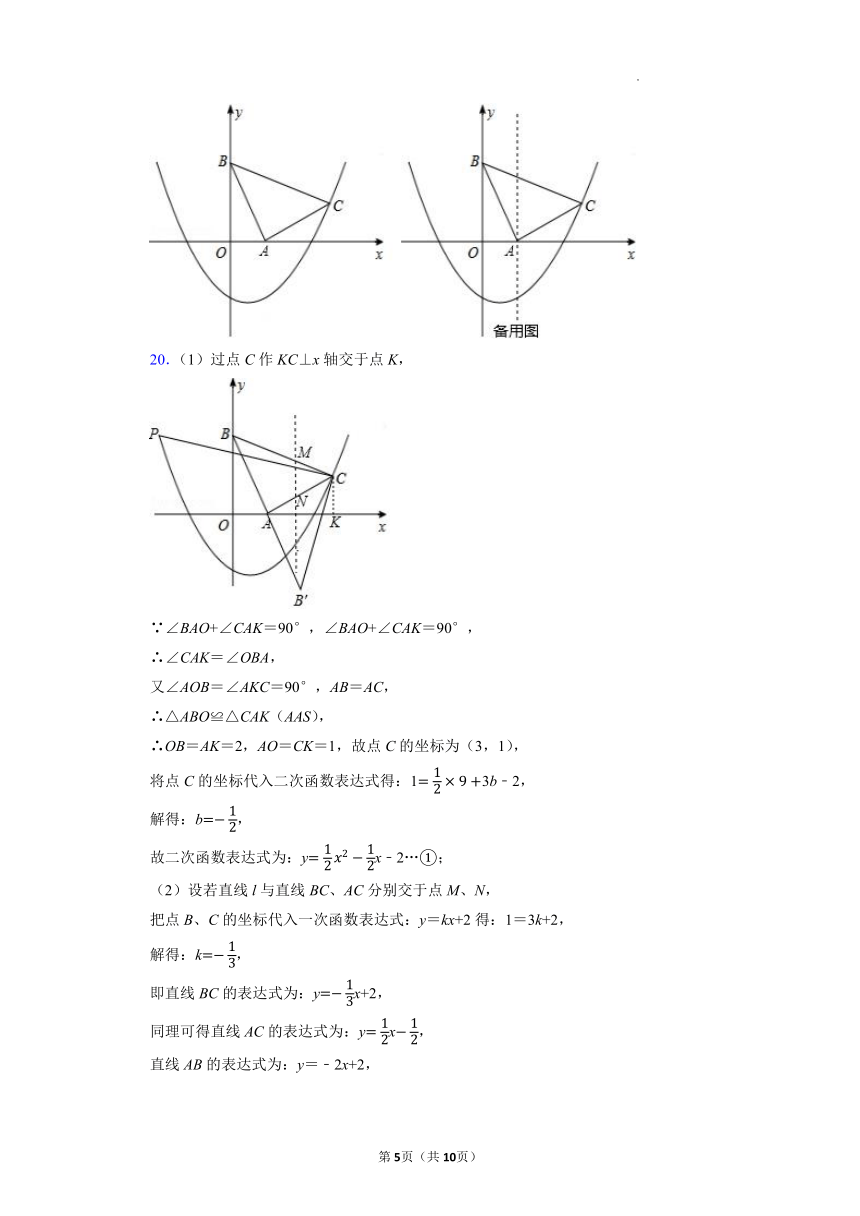
20.(1)过点C作KC⊥x轴交于点K,
∵∠BAO+∠CAK=90°,∠BAO+∠CAK=90°,
∴∠CAK=∠OBA,
又∠AOB=∠AKC=90°,AB=AC,
∴△ABO≌△CAK(AAS),
∴OB=AK=2,AO=CK=1,故点C的坐标为(3,1),
将点C的坐标代入二次函数表达式得:13b﹣2,
解得:b,
故二次函数表达式为:yx﹣2…①;
(2)设若直线l与直线BC、AC分别交于点M、N,
把点B、C的坐标代入一次函数表达式:y=kx+2得:1=3k+2,
解得:k,
即直线BC的表达式为:yx+2,
同理可得直线AC的表达式为:yx,
直线AB的表达式为:y=﹣2x+2,
设点M的坐标为(x,x+2)、点N坐标为(x,x),
直线l恰好将△ABC的面积分为1:2两部分,
设:S△CMNS△ACB,
即:(3﹣x)(x+2x),
解得x=3,
即:直线l与x轴的交点坐标为(3,0)或(3,0);
(3)将△ABC以AC所在直线为对称轴翻折180°,点B′的坐标为(2,﹣2),
①当∠PCB′=90°时,
∵∠BCB′=90°,故点P为直线BC与抛物线的另外一个交点,
直线BC的方程为:y②,
联立①②解得:x=3或,
故点P的坐标为(,);
②当∠CPB′=90°时,
同理可得:点P的坐标为(﹣1,﹣1)或(,),
故:点P的坐标为:(,)或(﹣1,﹣1)或(,).
【参考答案】
1.B.
2.C.
3.B.
4.三.
5.﹣1.
6.y=﹣3x2+6x﹣4.
7.3.
8.(1)由于A(﹣1,0)在一次函数y1=﹣x+m的图象上,得:
﹣(﹣1)+m=0,即m=﹣1;
已知A(﹣1,0)、B(2,﹣3)在二次函数y2=ax2+bx﹣3的图象上,则有:
,解得;
∴二次函数的解析式为y2=x2﹣2x﹣3;
(2)由两个函数的图象知:当y1>y2时,﹣1<x<2.
9.(1)y=x2+2x+3=(x+1)2+2,则抛物线的顶点坐标为(﹣1,2),把点(﹣1,2)向上平移2个单位长度,再向左平移3个单位长度得到点的坐标为(﹣4,4),所以平移后新抛物线的解析式为y=(x+4)2+4=x2+8x+20;
(2)y=x2+4x+3=(x+2)2﹣1,则抛物线的顶点坐标为(﹣2,﹣1),点(﹣2,﹣1)关于直线x=1对称的点的坐标为(4,﹣1),所以新抛物线的解析式为y=(x﹣4)2﹣1=x2﹣8x+15.
10.(1)由题意得,
解得,
∴抛物线为yx2﹣x,
∵该抛物线平移使得其经过原点,且对称轴不变,
∴平移后的抛物线为yx2﹣x,
将M(1,1)代入y=kx得k=1;
(2)过P作PQ∥y轴,交MN于Q,设Q(t,t),则P(t,t2﹣t),
则PQ=t﹣(t2﹣t)t2+2t,
∴SPQ×(3﹣1)=PQt2+2t(t﹣2)2,
∴当t=2时,△PMN的面积最大,此时P(2,),S△PMN.
11.D.
12.D.
13.D.
14.或6.提示:若x≤2,当y=12时,2x2+2=12,
解得:x1,x2(舍去);
若x>2,当y=12时,2x=12,
解得:x=6.
15.18.
16.(﹣2,﹣7).提示:∵点A(3,3)在二次函数y=x2+bx﹣9的图象上,
∴9+3b﹣9=3,
解得b=1,
∴二次函数为y=x2+x﹣9,
过B作BF⊥AC于F,过F作FD⊥y轴于D,过A作AE⊥DF于E,则△ABF为等腰直角三角形,易得△AEF≌△FDB(AAS),设BD=a,则EF=a,
∵点A(3,3)和点B(0,2),
∴DF=3﹣a=AE,OD=OB﹣BD=2﹣a,
∵AE+OD=3,
∴3﹣a+2﹣a=3,
解得a=1,
∴F(2,1),
设直线AC的解析式为y=kx+b,则,解得,
∴y=2x﹣3,
解方程组,可得或,
∴C(﹣2,﹣7),
17.(1,1).提示:在y=x2﹣mx+m=(-x+1)m+x2中,当x=1时,y=1,
∴无论m如何变化,图象总经过定点(1,1),
18.(1)由题意可知对称轴x4,
∴a=8.
(2)观察图象可知符合条件的m的值为m<3或m>5.
(3)由题意可知抛物线与直线y=2x没有交点,
即方程﹣x2+8x+b=2x没实数根,
整理得x2﹣6x﹣b=0,△=(﹣6)2+4b<0,
解得b<﹣9,
故b的取值范围为b<﹣9.
19.(1)把A(﹣2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c得,,
解得:,
∴该抛物线的解析式为:yx2+x+4;
(2)∵x1,
∴D(1,0),
∵点E为对称轴上一点,
∴设E(1,m),
则DE=|m|,
∵将线段ED绕点E顺时针方向旋转90°得到线段EF,
∴∠FED=90°,EF=DE=|m|,
当点E在x轴的上面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m(1﹣m)2+(1﹣m)+4,
解得:m=﹣1,m=﹣1,(不合题意,舍去),
当点E在x轴的下面,
∴F(1+m,﹣m),
∵点F恰好在该抛物线上,
∴﹣m(1+m)2+1+m+4,
解得:m=1,m=1(不合题意舍去),
∴线段DE的长为:1或1.
日期:2019/11/8 0:19:51;用户:zhuangqg68;邮箱:zhuangqg6855@;学号:3727759第10页(共10页)
1.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 …
y … ﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …
则该函数图象的对称轴是( )
A.直线x=﹣3 B.直线x=﹣2 C.直线x=﹣1 D.直线x=0
2.若点(﹣3,y1)、(1,y2)、(3,y3)都在二次函数y=(x+1)2+k的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1=y3>y2 C.y1=y2<y3 D.y1=y2>y3
3.抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )
A.b=2,c=﹣6 B.b=2,c=0 C.b=﹣6,c=8 D.b=﹣6,c=2
7.已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x ﹣3 0 3
y 0 3 3
则函数y=ax+bc不经过的象限是第_______象限.
5.若二次函数y=(a﹣1)x2+3x+a2﹣1的图象经过原点,则a的值必为_____.
6.将抛物线y=3x2﹣6x+5绕顶点旋转180°,再沿对称轴平移,得到一条与直线y=﹣x﹣2交于点(2,m)的新抛物线,新抛物线的解析式为__________ .
7.当x=a与x=b(a≠b)时,代数式x2﹣2x+3的值相等,则x=a+b时,代数式x2﹣2x+3的值为_____.
8.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
9.(1)将抛物线y=x2+2x+3向上平移2个单位长度,再向左平移3个单位长度,求平移后新抛物线的解析式;
(2)将抛物线y=x2+4x+3沿直线x=1翻折,得到一条新的抛物线,求新抛物线的解析式.
10.如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
(1)若将该抛物线平移使得其经过原点,且对称轴不变,求平移后的抛物线的表达式及k的值.
(2)设P为直线y=kx下方的抛物线上一点,求△PMN面积的最大值及此时P点的坐标.
11.将抛物线y=x2+3x+2向右平移a单位正好经过原点,则a的值为( )
A.a=1 B.a=2 C.a=﹣1或a=1 D.a=1或a=2
12.在同一坐标系中,函数y=ax2+b与y=bx2+ax的图象只可能是( )
A. B.
C. D.
13.(2018 禅城区一模)如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
14.若函数y,则当函数值y=12时,自变量x的值是__________.
15.如图,在平面直角坐标系中,点A是抛物线y=ax2﹣6ax+9a+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形的周长为_____.
16.如图,已知点A(3,3),点B(0,2),点A在二次函数y=x2+bx﹣9的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交二次函数图象于点C,则点C的坐标为__________.
17.某数学兴趣小组研究二次函数y=x2﹣mx+m的图象时发现:无论m如何变化,该图象总经过一个定点,这个定点的坐标是_______________.
18.已知二次函数y=﹣x2+ax+b的图象经过点A(x1,y1),B(x2,y2),且当x1=2,x2=6时,y1=y2.
(1)求a的值;
(2)若P(m,n1),Q(3,n2)也是二次函数图象上的两个点,且n1<n2,求实数m的取值范围;
(3)若T(t,2t)不在抛物线上,求b的取值范围.
19.如图所示,抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)、C(0,4)三点,抛物线对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E为对称轴上一点,将线段ED绕点E顺时针方向旋转90°得到线段EF,若点F恰好在该抛物线上,求线段DE的长.
20.如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数ybx﹣2的图象经过C点.
(1)求二次函数的解析式;
(2)平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;
(3)将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P点坐标;若不存在,请说明理由.
20.(1)过点C作KC⊥x轴交于点K,
∵∠BAO+∠CAK=90°,∠BAO+∠CAK=90°,
∴∠CAK=∠OBA,
又∠AOB=∠AKC=90°,AB=AC,
∴△ABO≌△CAK(AAS),
∴OB=AK=2,AO=CK=1,故点C的坐标为(3,1),
将点C的坐标代入二次函数表达式得:13b﹣2,
解得:b,
故二次函数表达式为:yx﹣2…①;
(2)设若直线l与直线BC、AC分别交于点M、N,
把点B、C的坐标代入一次函数表达式:y=kx+2得:1=3k+2,
解得:k,
即直线BC的表达式为:yx+2,
同理可得直线AC的表达式为:yx,
直线AB的表达式为:y=﹣2x+2,
设点M的坐标为(x,x+2)、点N坐标为(x,x),
直线l恰好将△ABC的面积分为1:2两部分,
设:S△CMNS△ACB,
即:(3﹣x)(x+2x),
解得x=3,
即:直线l与x轴的交点坐标为(3,0)或(3,0);
(3)将△ABC以AC所在直线为对称轴翻折180°,点B′的坐标为(2,﹣2),
①当∠PCB′=90°时,
∵∠BCB′=90°,故点P为直线BC与抛物线的另外一个交点,
直线BC的方程为:y②,
联立①②解得:x=3或,
故点P的坐标为(,);
②当∠CPB′=90°时,
同理可得:点P的坐标为(﹣1,﹣1)或(,),
故:点P的坐标为:(,)或(﹣1,﹣1)或(,).
【参考答案】
1.B.
2.C.
3.B.
4.三.
5.﹣1.
6.y=﹣3x2+6x﹣4.
7.3.
8.(1)由于A(﹣1,0)在一次函数y1=﹣x+m的图象上,得:
﹣(﹣1)+m=0,即m=﹣1;
已知A(﹣1,0)、B(2,﹣3)在二次函数y2=ax2+bx﹣3的图象上,则有:
,解得;
∴二次函数的解析式为y2=x2﹣2x﹣3;
(2)由两个函数的图象知:当y1>y2时,﹣1<x<2.
9.(1)y=x2+2x+3=(x+1)2+2,则抛物线的顶点坐标为(﹣1,2),把点(﹣1,2)向上平移2个单位长度,再向左平移3个单位长度得到点的坐标为(﹣4,4),所以平移后新抛物线的解析式为y=(x+4)2+4=x2+8x+20;
(2)y=x2+4x+3=(x+2)2﹣1,则抛物线的顶点坐标为(﹣2,﹣1),点(﹣2,﹣1)关于直线x=1对称的点的坐标为(4,﹣1),所以新抛物线的解析式为y=(x﹣4)2﹣1=x2﹣8x+15.
10.(1)由题意得,
解得,
∴抛物线为yx2﹣x,
∵该抛物线平移使得其经过原点,且对称轴不变,
∴平移后的抛物线为yx2﹣x,
将M(1,1)代入y=kx得k=1;
(2)过P作PQ∥y轴,交MN于Q,设Q(t,t),则P(t,t2﹣t),
则PQ=t﹣(t2﹣t)t2+2t,
∴SPQ×(3﹣1)=PQt2+2t(t﹣2)2,
∴当t=2时,△PMN的面积最大,此时P(2,),S△PMN.
11.D.
12.D.
13.D.
14.或6.提示:若x≤2,当y=12时,2x2+2=12,
解得:x1,x2(舍去);
若x>2,当y=12时,2x=12,
解得:x=6.
15.18.
16.(﹣2,﹣7).提示:∵点A(3,3)在二次函数y=x2+bx﹣9的图象上,
∴9+3b﹣9=3,
解得b=1,
∴二次函数为y=x2+x﹣9,
过B作BF⊥AC于F,过F作FD⊥y轴于D,过A作AE⊥DF于E,则△ABF为等腰直角三角形,易得△AEF≌△FDB(AAS),设BD=a,则EF=a,
∵点A(3,3)和点B(0,2),
∴DF=3﹣a=AE,OD=OB﹣BD=2﹣a,
∵AE+OD=3,
∴3﹣a+2﹣a=3,
解得a=1,
∴F(2,1),
设直线AC的解析式为y=kx+b,则,解得,
∴y=2x﹣3,
解方程组,可得或,
∴C(﹣2,﹣7),
17.(1,1).提示:在y=x2﹣mx+m=(-x+1)m+x2中,当x=1时,y=1,
∴无论m如何变化,图象总经过定点(1,1),
18.(1)由题意可知对称轴x4,
∴a=8.
(2)观察图象可知符合条件的m的值为m<3或m>5.
(3)由题意可知抛物线与直线y=2x没有交点,
即方程﹣x2+8x+b=2x没实数根,
整理得x2﹣6x﹣b=0,△=(﹣6)2+4b<0,
解得b<﹣9,
故b的取值范围为b<﹣9.
19.(1)把A(﹣2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c得,,
解得:,
∴该抛物线的解析式为:yx2+x+4;
(2)∵x1,
∴D(1,0),
∵点E为对称轴上一点,
∴设E(1,m),
则DE=|m|,
∵将线段ED绕点E顺时针方向旋转90°得到线段EF,
∴∠FED=90°,EF=DE=|m|,
当点E在x轴的上面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m(1﹣m)2+(1﹣m)+4,
解得:m=﹣1,m=﹣1,(不合题意,舍去),
当点E在x轴的下面,
∴F(1+m,﹣m),
∵点F恰好在该抛物线上,
∴﹣m(1+m)2+1+m+4,
解得:m=1,m=1(不合题意舍去),
∴线段DE的长为:1或1.
日期:2019/11/8 0:19:51;用户:zhuangqg68;邮箱:zhuangqg6855@;学号:3727759第10页(共10页)
