2021—2022学年北师大版数学九年级下册2.2二次函数y=ax2的函数图像和性质课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.2二次函数y=ax2的函数图像和性质课时对应练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 120.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 17:19:39 | ||
图片预览


文档简介
第02课时 二次函数y=ax2的函数图像和性质
1.对于函数y=x2,下列判断中,正确的是( )
A.若m、n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任何实数x,都有y>0
2.如图,在同一直角坐标系中,作出函数①y=3x2;②y;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
A.①②③ B.①③② C.②③① D.③②①
3.已知(x1,y1),(x2,y2)是抛物线y=ax2(a≠0)上的两点.当x2<x1<0时,y2<y1,则a的取值范围是 .
4.二次函数y=x2的图象对称轴左侧上有两点A(a,4),B(b,),则a b.(选填“>”、“<”或“=”)
5.如图,⊙O的半径为2,C1是函数yx2的图象,C2是函数yx2的图象,则阴影部分的面积是 .
6.函数y=(m﹣3)为二次函数.
(1)若其图象开口向上,求函数关系式;
(2)若当x>0时,y随x的增大而减小,求函数的关系式,并画出函数的图象.
7.如图所示,已知抛物线y=x2上有一点A.点A的横坐标是﹣1,过点A作AB∥x轴.交抛物线于另一点B.求△AOB的面积.
8.一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣x2 B.y=2x2 C. D.
9.已知a>0,在同一直角坐标系中,函数y=ax与y=﹣ax2的图象有可能是( )
A. B.
C. D.
10.已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为: .
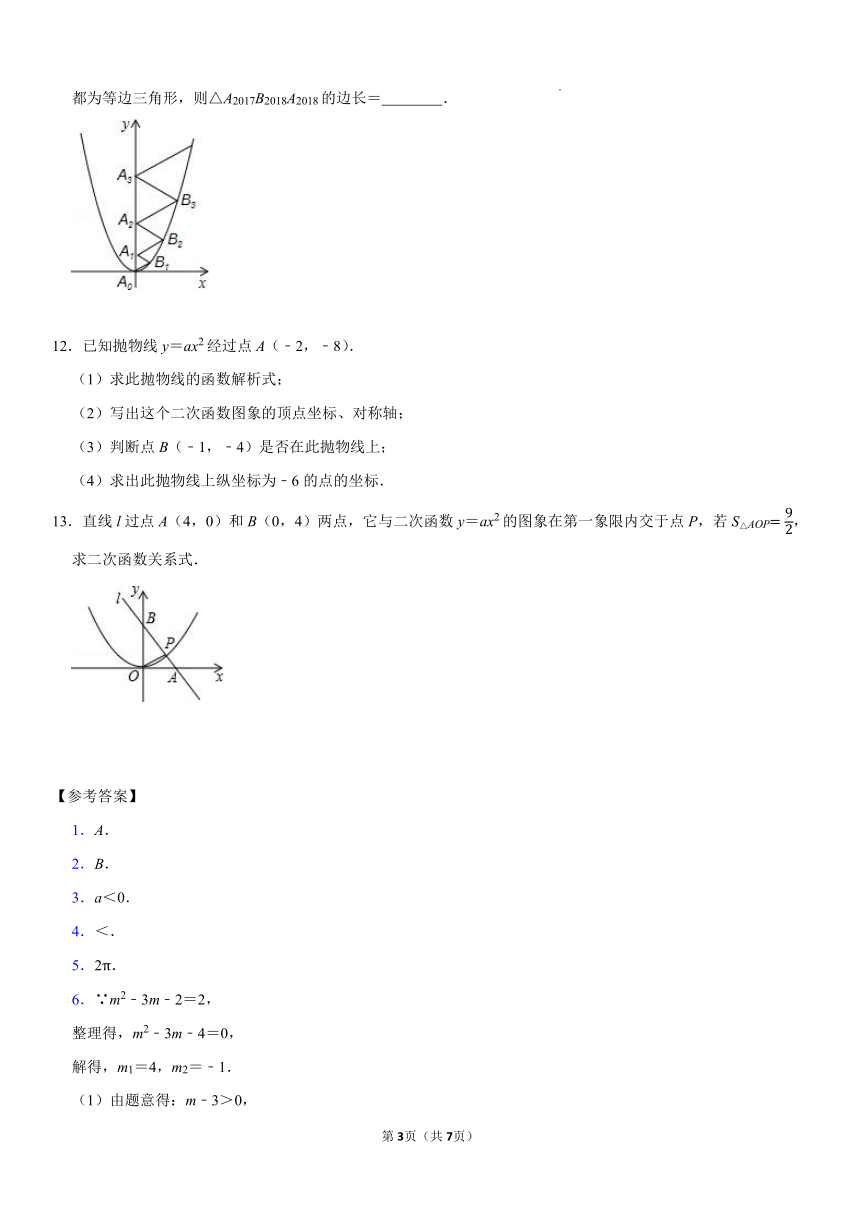
11.二次函数yx2的图象如图所示,点A0位于坐标原点,点A1、A2、A3、…、A2018在y轴的正半轴上,点B1、B2、B3、…、B2018在二次函数yx2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A2017B2018A2018的边长= .
12.已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)求此抛物线的函数解析式;
(2)写出这个二次函数图象的顶点坐标、对称轴;
(3)判断点B(﹣1,﹣4)是否在此抛物线上;
(4)求出此抛物线上纵坐标为﹣6的点的坐标.
13.直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP,求二次函数关系式.
【参考答案】
1.A.
2.B.
3.a<0.
4.<.
5.2π.
6.∵m2﹣3m﹣2=2,
整理得,m2﹣3m﹣4=0,
解得,m1=4,m2=﹣1.
(1)由题意得:m﹣3>0,
解得m>3,
∴m=4.
∴函数关系式为y=x2.
(2)∵当x>0时,y随x的增大而减小,
∴m﹣3<0,
∴m<3,
∴m=﹣1,
∴函数关系式为y=﹣4x2.
画出函数的图象如图:
7.∵抛物线y=x2上有一点A.点A的横坐标是﹣1,
∴y=1,
∴A(﹣1,1),
∵B是A的对称点,
∴B(1,1),
∴AB=2,
∴△AOB的面积AB OC2×1=1.
8.C.
9.D.
10.x2.
11.2018.提示:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
设A0A1=a,A1A2=b,A2A3=c,则AB1a,BB2b,CB3c,
在正△A0B1A1中,B1(a,),
代入yx2中,得a2,解得a=1,即A0A1=1,
在正△A1B2A2中,B2(b,1),
代入yx2中,得1b2,解得b=2,即A1A2=2,
在正△A2B3A3中,B3(c,3),
代入yx2中,得3c)2,解得c=3,即A2A3=3,
…
依此类推由此可得△A2017B2018A2018的边长=2018。
故答案为:2018.
12.(1)∵抛物线y=ax2经过点A(﹣2,﹣8),
∴a (﹣2)2=﹣8,
∴a=﹣2,
∴此抛物线对应的函数解析式为y=﹣2x2.
(2)由题可得,抛物线的顶点坐标为(0,0),对称轴为y轴;
(3)把x=﹣1代入得,y=﹣2×(﹣1)2=﹣2≠﹣4,
∴点B(﹣1,﹣4)不在此抛物线上;
(4)把y=﹣6代入y=﹣2x2得,﹣6=﹣2x2,
解得x=±,
∴抛物线上纵坐标为﹣6的点的坐标为(,﹣6)或(,﹣6).
13.设直线为:y=kx+b,
∵直线l过点A(4,0)和B(0,4)两点,
∴4k+b=0,b=4
∴y=﹣x+4,
∵S△AOP,
∴4×yp,
∴yp,
∴x+4,
解得x,
把点P的坐标(,)代入y=ax2,
解得a,
∴y.
第2页(共2页)
1.对于函数y=x2,下列判断中,正确的是( )
A.若m、n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任何实数x,都有y>0
2.如图,在同一直角坐标系中,作出函数①y=3x2;②y;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
A.①②③ B.①③② C.②③① D.③②①
3.已知(x1,y1),(x2,y2)是抛物线y=ax2(a≠0)上的两点.当x2<x1<0时,y2<y1,则a的取值范围是 .
4.二次函数y=x2的图象对称轴左侧上有两点A(a,4),B(b,),则a b.(选填“>”、“<”或“=”)
5.如图,⊙O的半径为2,C1是函数yx2的图象,C2是函数yx2的图象,则阴影部分的面积是 .
6.函数y=(m﹣3)为二次函数.
(1)若其图象开口向上,求函数关系式;
(2)若当x>0时,y随x的增大而减小,求函数的关系式,并画出函数的图象.
7.如图所示,已知抛物线y=x2上有一点A.点A的横坐标是﹣1,过点A作AB∥x轴.交抛物线于另一点B.求△AOB的面积.
8.一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣x2 B.y=2x2 C. D.
9.已知a>0,在同一直角坐标系中,函数y=ax与y=﹣ax2的图象有可能是( )
A. B.
C. D.
10.已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为: .
11.二次函数yx2的图象如图所示,点A0位于坐标原点,点A1、A2、A3、…、A2018在y轴的正半轴上,点B1、B2、B3、…、B2018在二次函数yx2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A2017B2018A2018的边长= .
12.已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)求此抛物线的函数解析式;
(2)写出这个二次函数图象的顶点坐标、对称轴;
(3)判断点B(﹣1,﹣4)是否在此抛物线上;
(4)求出此抛物线上纵坐标为﹣6的点的坐标.
13.直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP,求二次函数关系式.
【参考答案】
1.A.
2.B.
3.a<0.
4.<.
5.2π.
6.∵m2﹣3m﹣2=2,
整理得,m2﹣3m﹣4=0,
解得,m1=4,m2=﹣1.
(1)由题意得:m﹣3>0,
解得m>3,
∴m=4.
∴函数关系式为y=x2.
(2)∵当x>0时,y随x的增大而减小,
∴m﹣3<0,
∴m<3,
∴m=﹣1,
∴函数关系式为y=﹣4x2.
画出函数的图象如图:
7.∵抛物线y=x2上有一点A.点A的横坐标是﹣1,
∴y=1,
∴A(﹣1,1),
∵B是A的对称点,
∴B(1,1),
∴AB=2,
∴△AOB的面积AB OC2×1=1.
8.C.
9.D.
10.x2.
11.2018.提示:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
设A0A1=a,A1A2=b,A2A3=c,则AB1a,BB2b,CB3c,
在正△A0B1A1中,B1(a,),
代入yx2中,得a2,解得a=1,即A0A1=1,
在正△A1B2A2中,B2(b,1),
代入yx2中,得1b2,解得b=2,即A1A2=2,
在正△A2B3A3中,B3(c,3),
代入yx2中,得3c)2,解得c=3,即A2A3=3,
…
依此类推由此可得△A2017B2018A2018的边长=2018。
故答案为:2018.
12.(1)∵抛物线y=ax2经过点A(﹣2,﹣8),
∴a (﹣2)2=﹣8,
∴a=﹣2,
∴此抛物线对应的函数解析式为y=﹣2x2.
(2)由题可得,抛物线的顶点坐标为(0,0),对称轴为y轴;
(3)把x=﹣1代入得,y=﹣2×(﹣1)2=﹣2≠﹣4,
∴点B(﹣1,﹣4)不在此抛物线上;
(4)把y=﹣6代入y=﹣2x2得,﹣6=﹣2x2,
解得x=±,
∴抛物线上纵坐标为﹣6的点的坐标为(,﹣6)或(,﹣6).
13.设直线为:y=kx+b,
∵直线l过点A(4,0)和B(0,4)两点,
∴4k+b=0,b=4
∴y=﹣x+4,
∵S△AOP,
∴4×yp,
∴yp,
∴x+4,
解得x,
把点P的坐标(,)代入y=ax2,
解得a,
∴y.
第2页(共2页)
