2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(1)课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(1)课时对应练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 17:19:48 | ||
图片预览



文档简介
第03课时 二次函数y=a(x-h)2+k的函数图像和性质(1)
1.关于二次函数y=﹣2x2+1,以下说法正确的是( )
A.开口方向向上
B.顶点坐标是(﹣2,1)
C.当x<0时,y随x的增大而增大
D.当x=0时,y有最大值
2.如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+3
3.二次函数y=3x2﹣3的图象开口向_______,顶点坐标为 _______ ,对称轴为 _______,当x>0时,y随x的增大而 _______;当x<0时,则y随x的增大而 _______ .当a=3>0,则y有最_______值,当x=_______时,y的最_______值是 ____ .
4.二次函数y=2x2+3的图象与y轴的交点坐标为 _______ .
5.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_______n(填“<”或“=”或“>”).
6.已知二次函数y=2x2﹣3的图象经过(x1,5),(x2,5)(x1≠x2),则当x取(x1+x2)时,函数值为_______ .
7.抛物线y=2x2﹣m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.
8.如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以点A为顶点的抛物线经过点C
(1)求抛物线的函数表达式;
(2)将矩形ABCO绕点A旋转,得到矩形AB′C′O′,使点C′落在x轴上,抛物线是否经过点C′?请说明理由.
9.二次函数y=2x2﹣3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
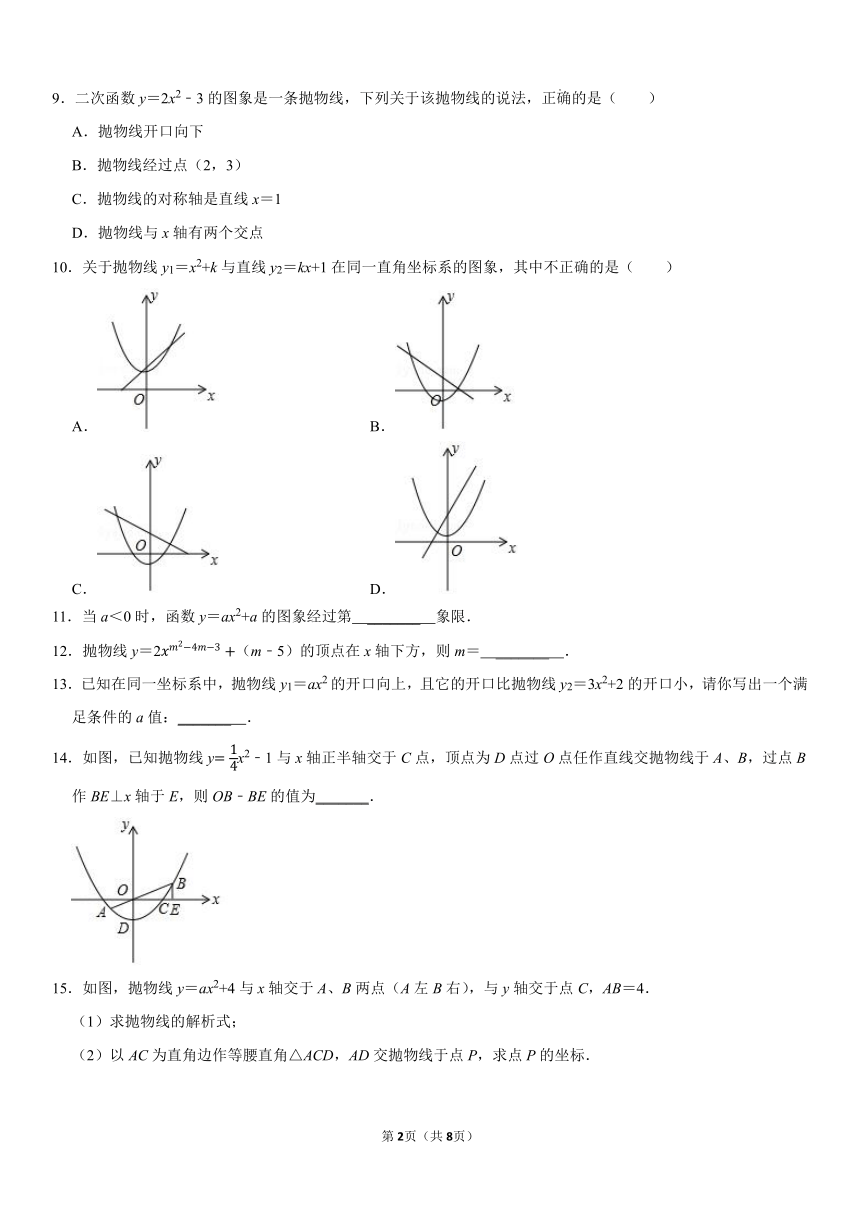
10.关于抛物线y1=x2+k与直线y2=kx+1在同一直角坐标系的图象,其中不正确的是( )
A. B.
C. D.
11.当a<0时,函数y=ax2+a的图象经过第 _______ 象限.
12.抛物线y=2(m﹣5)的顶点在x轴下方,则m= _______ .
13.已知在同一坐标系中,抛物线y1=ax2的开口向上,且它的开口比抛物线y2=3x2+2的开口小,请你写出一个满足条件的a值:_______ .
14.如图,已知抛物线yx2﹣1与x轴正半轴交于C点,顶点为D点过O点任作直线交抛物线于A、B,过点B作BE⊥x轴于E,则OB﹣BE的值为_______.
15.如图,抛物线y=ax2+4与x轴交于A、B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的解析式;
(2)以AC为直角边作等腰直角△ACD,AD交抛物线于点P,求点P的坐标.
16.如图,已知二次函数y=x2﹣4,将x轴下方的图象沿x轴翻折,得到一个新图象(图中的实线).根据新图象回答问题:
(1)当x=________时,函数y有最小值.
(2)当y随x的增大而增大时,自变量x的范围是 ________ .
(3)当a<4时,探究一次函数y=2x+a的图象与新图象公共点的个数情况.
【参考答案】
1.C.
2.C.
3.上,(0,﹣3),y轴,增大,减小,小,0,小,﹣3.
4.(0,3).
5.>.
6.﹣3.
7.∵抛物线与x轴交于点A、B,与y轴交于点C,
∴A(,0),B(,0),C(0,﹣m),
又∵∠ACB=90°,且y轴是抛物线的对称轴,
∴△ABC是等腰直角三角形,
∴OA=OB=OC,
∴m,即m2,解得m=0(不合题意,舍去)或m,
∴y=2x2.
8.(1)∵OA=2,
∴抛物线顶点坐标A是(0,2),C(﹣1,0),
∴设抛物线解析式为y=ax2+2,把点C(﹣1,0)代入,得
0=a+2,
解得a=﹣2.
则该抛物线解析式为:y=﹣2x2+2;
(2)如图,连接AC,AC′.
根据旋转的性质得到AC=AC′,OA⊥CC′,即点C与C′关于y轴对称,
又因为该抛物线的对称轴是y轴,点C在该抛物线线上,
所以抛物线经过点C′.
9.D.
10.D.
11.三、四.
12.﹣1.
13.4(答案不唯一).
14.2.
15.(1)∵抛物线y=ax2+4与x轴交于A、B两点(A左B右),与y轴交于点C,
∴C(0,4),
∵AB=4,
∴A(﹣2,0),B(2,0),
∴4a+4=0,解得a=﹣1,
∴抛物线的解析式为y=﹣x2+4;
(2)方法一:设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣2,0),C(0,4),
∴,解得,
∴直线AC的解析式为y=2x+4,AC2,
当CD⊥AC时,
设直线CD的解析式为yx+a,
∵C(0,4),
∴a=4,
∴直线CD的解析式为yx+4,
设D(x,x+4),
∵AC=CD,
∴CD2=AC2,即x2+(x)2=20,解得x=4或x=﹣4(舍去)
∴D(4,2),
设直线AD的解析式为y=k1x+b1,
∴,解得,
∴直线AD的解析式为yx,
∴,解得或(舍去),
∴P(,);
当AD⊥AC时,同理可设直线AD的解析式为yx+m,
∵A(﹣2,0),
∴1+m=0,解得m=﹣1,
∴直线AD的解析式为yx﹣1,
∴设P(x,x﹣1),
∵AC=AD,
∴(x+2)2+(x﹣1)2=20,解得x=﹣6或x=2(舍去).
∴此种情况不存在.
故P点坐标为(,).
方法二:过点D作DE垂直y轴,
∵∠ACO+∠DCO=90°,∠DCE+∠CDE=90°,
∴∠ACO=∠CDE,
在△AOC和△CED中
∴△AOC≌△CED(AAS),
∴CO=ED=4,CE=AO=2,
∴D(4,2),
将A(﹣2,0),D(4,2)代入y=kx+b得:
,
解得:,
∴AP所在解析式为:yx,
∴将两函数联立得:,
解得:,(不合题意舍去),
∴故P点坐标为(,).
16.(1)∵由函数图象可知,当x=﹣2或x=2时y最小等于0,
∴当x=﹣2或x=2时,函数y有最小值.
故答案为:x=﹣2或x=2;
(2)∵由函数图象可知当﹣2<x<0或x>2时y随x的增大而增大,
∴x的取值范围是:﹣2<x<0或x>2,
故答案为:﹣2<x<0或x>2;
(3)∵一次函数y=2x+a与x轴的交点为(,0),与y轴的交点为(0,a),
∴当a<﹣4时,没有交点;
当a=﹣4时,有1个交点;
当﹣4<a<4时,有2个交点.
第7页(共7页)
1.关于二次函数y=﹣2x2+1,以下说法正确的是( )
A.开口方向向上
B.顶点坐标是(﹣2,1)
C.当x<0时,y随x的增大而增大
D.当x=0时,y有最大值
2.如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+3
3.二次函数y=3x2﹣3的图象开口向_______,顶点坐标为 _______ ,对称轴为 _______,当x>0时,y随x的增大而 _______;当x<0时,则y随x的增大而 _______ .当a=3>0,则y有最_______值,当x=_______时,y的最_______值是 ____ .
4.二次函数y=2x2+3的图象与y轴的交点坐标为 _______ .
5.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_______n(填“<”或“=”或“>”).
6.已知二次函数y=2x2﹣3的图象经过(x1,5),(x2,5)(x1≠x2),则当x取(x1+x2)时,函数值为_______ .
7.抛物线y=2x2﹣m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.
8.如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以点A为顶点的抛物线经过点C
(1)求抛物线的函数表达式;
(2)将矩形ABCO绕点A旋转,得到矩形AB′C′O′,使点C′落在x轴上,抛物线是否经过点C′?请说明理由.
9.二次函数y=2x2﹣3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
10.关于抛物线y1=x2+k与直线y2=kx+1在同一直角坐标系的图象,其中不正确的是( )
A. B.
C. D.
11.当a<0时,函数y=ax2+a的图象经过第 _______ 象限.
12.抛物线y=2(m﹣5)的顶点在x轴下方,则m= _______ .
13.已知在同一坐标系中,抛物线y1=ax2的开口向上,且它的开口比抛物线y2=3x2+2的开口小,请你写出一个满足条件的a值:_______ .
14.如图,已知抛物线yx2﹣1与x轴正半轴交于C点,顶点为D点过O点任作直线交抛物线于A、B,过点B作BE⊥x轴于E,则OB﹣BE的值为_______.
15.如图,抛物线y=ax2+4与x轴交于A、B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的解析式;
(2)以AC为直角边作等腰直角△ACD,AD交抛物线于点P,求点P的坐标.
16.如图,已知二次函数y=x2﹣4,将x轴下方的图象沿x轴翻折,得到一个新图象(图中的实线).根据新图象回答问题:
(1)当x=________时,函数y有最小值.
(2)当y随x的增大而增大时,自变量x的范围是 ________ .
(3)当a<4时,探究一次函数y=2x+a的图象与新图象公共点的个数情况.
【参考答案】
1.C.
2.C.
3.上,(0,﹣3),y轴,增大,减小,小,0,小,﹣3.
4.(0,3).
5.>.
6.﹣3.
7.∵抛物线与x轴交于点A、B,与y轴交于点C,
∴A(,0),B(,0),C(0,﹣m),
又∵∠ACB=90°,且y轴是抛物线的对称轴,
∴△ABC是等腰直角三角形,
∴OA=OB=OC,
∴m,即m2,解得m=0(不合题意,舍去)或m,
∴y=2x2.
8.(1)∵OA=2,
∴抛物线顶点坐标A是(0,2),C(﹣1,0),
∴设抛物线解析式为y=ax2+2,把点C(﹣1,0)代入,得
0=a+2,
解得a=﹣2.
则该抛物线解析式为:y=﹣2x2+2;
(2)如图,连接AC,AC′.
根据旋转的性质得到AC=AC′,OA⊥CC′,即点C与C′关于y轴对称,
又因为该抛物线的对称轴是y轴,点C在该抛物线线上,
所以抛物线经过点C′.
9.D.
10.D.
11.三、四.
12.﹣1.
13.4(答案不唯一).
14.2.
15.(1)∵抛物线y=ax2+4与x轴交于A、B两点(A左B右),与y轴交于点C,
∴C(0,4),
∵AB=4,
∴A(﹣2,0),B(2,0),
∴4a+4=0,解得a=﹣1,
∴抛物线的解析式为y=﹣x2+4;
(2)方法一:设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣2,0),C(0,4),
∴,解得,
∴直线AC的解析式为y=2x+4,AC2,
当CD⊥AC时,
设直线CD的解析式为yx+a,
∵C(0,4),
∴a=4,
∴直线CD的解析式为yx+4,
设D(x,x+4),
∵AC=CD,
∴CD2=AC2,即x2+(x)2=20,解得x=4或x=﹣4(舍去)
∴D(4,2),
设直线AD的解析式为y=k1x+b1,
∴,解得,
∴直线AD的解析式为yx,
∴,解得或(舍去),
∴P(,);
当AD⊥AC时,同理可设直线AD的解析式为yx+m,
∵A(﹣2,0),
∴1+m=0,解得m=﹣1,
∴直线AD的解析式为yx﹣1,
∴设P(x,x﹣1),
∵AC=AD,
∴(x+2)2+(x﹣1)2=20,解得x=﹣6或x=2(舍去).
∴此种情况不存在.
故P点坐标为(,).
方法二:过点D作DE垂直y轴,
∵∠ACO+∠DCO=90°,∠DCE+∠CDE=90°,
∴∠ACO=∠CDE,
在△AOC和△CED中
∴△AOC≌△CED(AAS),
∴CO=ED=4,CE=AO=2,
∴D(4,2),
将A(﹣2,0),D(4,2)代入y=kx+b得:
,
解得:,
∴AP所在解析式为:yx,
∴将两函数联立得:,
解得:,(不合题意舍去),
∴故P点坐标为(,).
16.(1)∵由函数图象可知,当x=﹣2或x=2时y最小等于0,
∴当x=﹣2或x=2时,函数y有最小值.
故答案为:x=﹣2或x=2;
(2)∵由函数图象可知当﹣2<x<0或x>2时y随x的增大而增大,
∴x的取值范围是:﹣2<x<0或x>2,
故答案为:﹣2<x<0或x>2;
(3)∵一次函数y=2x+a与x轴的交点为(,0),与y轴的交点为(0,a),
∴当a<﹣4时,没有交点;
当a=﹣4时,有1个交点;
当﹣4<a<4时,有2个交点.
第7页(共7页)
