2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(2)课时对应练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.2二次函数y=a(x-h)2+k的函数图像和性质(2)课时对应练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 122.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 17:24:49 | ||
图片预览



文档简介
第04课时 二次函数y=a(x-h)2+k的函数图像和性质(2)
1.在下列二次函数中,其图象对称轴为x=﹣2的是( )
A.y=(x+2)2 B.y=2x2﹣2 C.y=﹣2x2﹣2 D.y=2(x﹣2)2
2.抛物线y=﹣2(x﹣3)2的顶点坐标和对称轴分别为( )
A.(﹣3,0),直线x=﹣3 B.(3,0),直线x=3
C.(0,﹣3),直线x=﹣3 D.(0,3),直线x=﹣3
3.顶点为(5,0)且开口方向、形状与函数yx2的图象相同的抛物线是( )
A.y(x﹣5)2 B.yx2﹣5
C.y(x+5)2 D.y(x+5)2
4.抛物线y=(x﹣5)2的开口______,对称轴是________,顶点坐标是________,它可以看做是由抛物线y=x2向________平移________个单位长度得到的.抛物线 ________ 向右平移3个单位长度即得到抛物线y=2(x﹣1)2.
5.对称轴为x=﹣2,顶点在x轴上,并与y轴交于点(0,3)的抛物线解析式为 ________ .
6.已知二次函数y=2(x﹣1)2的图象如图所示,则△ABO的面积是________。
7.已知抛物线y=a(x﹣h)2的对称轴为x=﹣2,且过点(1,﹣3).
(1)求抛物线的解析式;
(2)画出函数的图象;
(3)从图象上观察,当x取何值时,y随x的增大而增大?当x取何值时,函数有最大值(或最小值)?
8.如图,以边长为1的正方形ABCO的两边OA、OC所在直线为轴建立坐标系,点O为原点.
(1)求以A为顶点,且经过点C的抛物线解析式;
(2)求(1)中的抛物线与对角线OB交于点D的坐标.
9.二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
10.如图所示,在直角坐标系中,函数y=﹣x+1与y(x﹣1)2的图象大致是( )
A. B.
C. D.
11.若二次函数y=x2﹣mx+1的图象的顶点在x轴上,则m的值是( )
A.2 B.﹣2 C.0 D.±2
12.把抛物线y=2(x﹣3)2向左平移2个单位长度得到的抛物线解析式为 ________ .
13.已知二次函数y=3(x﹣1)2的图象上有三点A()、B(2,y2)、C(﹣5,y3),则y1、y2、y3的大小关系为________ .
14.若把抛物线y=a(x﹣4)2向左平移6个单位长度后得到抛物线y=﹣3(x﹣h)2,则a=________ ,h=________ .若抛物线y=a(x﹣4)2的顶点为A,且与y轴交于点B,抛物线y=﹣3(x+2)2的顶点为M,则S△MAB=________.
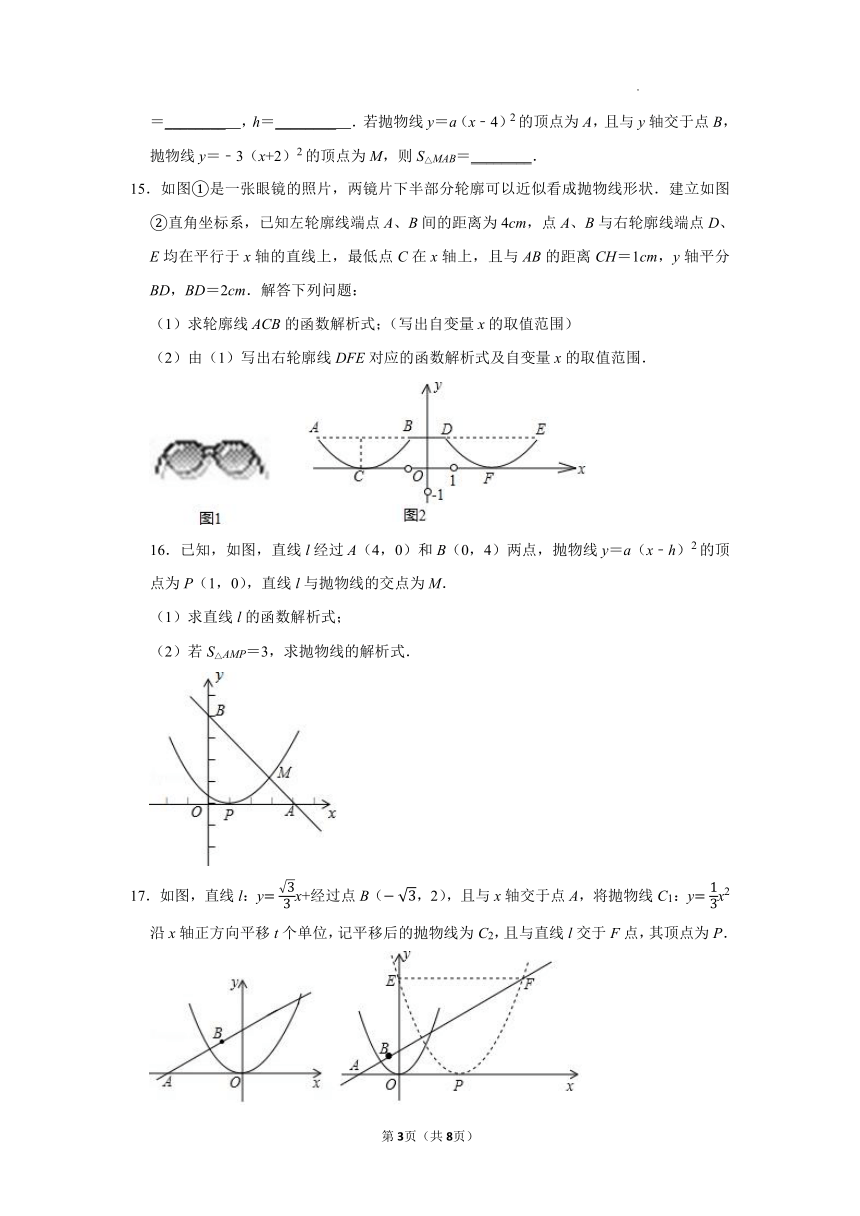
15.如图①是一张眼镜的照片,两镜片下半部分轮廓可以近似看成抛物线形状.建立如图②直角坐标系,已知左轮廓线端点A、B间的距离为4cm,点A、B与右轮廓线端点D、E均在平行于x轴的直线上,最低点C在x轴上,且与AB的距离CH=1cm,y轴平分BD,BD=2cm.解答下列问题:
(1)求轮廓线ACB的函数解析式;(写出自变量x的取值范围)
(2)由(1)写出右轮廓线DFE对应的函数解析式及自变量x的取值范围.
16.已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
17.如图,直线l:yx+经过点B(,2),且与x轴交于点A,将抛物线C1:yx2沿x轴正方向平移t个单位,记平移后的抛物线为C2,且与直线l交于F点,其顶点为P.
(1)当抛物线C2与直线l交于y轴上同一点时,求t的值;
(2)抛物线C2与y轴交于点E,与直线AB交于两点,其中一个交点为F.当线段EF∥x轴时,求平移后的抛物线C2对应的函数关系式.
【参考答案】
1.A.
2.B.
3.A.
4.向上,x=5,(5,0),右,5,y=2(x+2)2.
5.y.
6.1.
7.(1)∵x=﹣2为抛物线y=a(x﹣h)2的对称轴,
∴抛物线的解析式为:y=a(x+2)2,
将(1,﹣3)代入可得,
﹣3=a(1+2)2,
解得:a,
∴抛物线的解析式为:y(x+2)2;
(2)如图所示,
(3)∵该抛物线的对称轴为:x=﹣2,
∴顶点坐标为(﹣2,0),
根据抛物线的对称性得,当x<﹣2时,y随x的增大而增大,
∵0,
∴函数有最大值,
∴当x=﹣2时,函数有最大值是0.
8.(1)A的坐标是(1,0)、C坐标是(0,1),设出解析式是y=a(x﹣1)2,把C的坐标代入得:a(﹣1)2=1,
解得:a=1,
则抛物线的解析式是:y=(x﹣1)2;
(2)B的坐标是(1,1),
设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x.
根据题意得:,
解得:(舍去),或.
则D的坐标是:(,).
9.(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a,
∴二次函数解析式为y1(x﹣2)2a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:,
解得:k,b=﹣1,
则直线AB解析式为yx﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
10.B.
11.D.
12.y=2(x﹣1)2.
13.y1<y2<y3.
14.﹣3,﹣2,144.
15(1)y2(﹣5≤x≤﹣1);
(2)由左右两轮廓线关于y轴对称,
又y(x+3)2,顶点C(﹣3,0),
∴顶点C关于y轴对称点F(3,0)且a1,
∴右轮廓线DFE对应的函数解析式为y(x﹣3)2,即:yx2x(1≤x≤5).
16.(1)设一次函数解析式为y=kx+b,
把A(4,0),B(0,4)分别代入解析式得,
解得,
解析式为y=﹣x+4.
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴(4﹣1)n=3,
解得,n=2,
把M(m,2)代入为2=﹣m+4得,m=2,
M(2,2),
∵抛物线y=a(x﹣h)2的顶点为P(1,0),
可得y=a(x﹣1)2,
把M(2,2)代入y=a(x﹣1)2得,2=a(2﹣1)2,解得a=2,函数解析式为y=2(x﹣1)2.
17。解:(1)把B(,2)代入yx+b得()+b=2,解得b=3,
∴一次函数解析式为yx+3,
当x=0时,yx+3=3,则一次函数与y轴的交点坐标为(0,3),
yx2沿x轴正方向平移t个单位后所得抛物线解析式为y(x﹣t)2,
把(0,3)代入y(x﹣t)2得t1=3,t2=﹣3(舍去),
即t的值为3;
(2)当x=0时,y(x﹣t)2t2,则E(0,t2)
∵EF∥x轴,
而抛物线y(x﹣t)2的对称轴为直线x=t,
∴F点坐标为(2t,t2)
把F(2t,t2)代入yx+3得 2t+3t2,解得t1=3,t2(舍去),
∴平移后的抛物线C2对应的函数关系式为y(x﹣3)2.
第7页(共7页)
1.在下列二次函数中,其图象对称轴为x=﹣2的是( )
A.y=(x+2)2 B.y=2x2﹣2 C.y=﹣2x2﹣2 D.y=2(x﹣2)2
2.抛物线y=﹣2(x﹣3)2的顶点坐标和对称轴分别为( )
A.(﹣3,0),直线x=﹣3 B.(3,0),直线x=3
C.(0,﹣3),直线x=﹣3 D.(0,3),直线x=﹣3
3.顶点为(5,0)且开口方向、形状与函数yx2的图象相同的抛物线是( )
A.y(x﹣5)2 B.yx2﹣5
C.y(x+5)2 D.y(x+5)2
4.抛物线y=(x﹣5)2的开口______,对称轴是________,顶点坐标是________,它可以看做是由抛物线y=x2向________平移________个单位长度得到的.抛物线 ________ 向右平移3个单位长度即得到抛物线y=2(x﹣1)2.
5.对称轴为x=﹣2,顶点在x轴上,并与y轴交于点(0,3)的抛物线解析式为 ________ .
6.已知二次函数y=2(x﹣1)2的图象如图所示,则△ABO的面积是________。
7.已知抛物线y=a(x﹣h)2的对称轴为x=﹣2,且过点(1,﹣3).
(1)求抛物线的解析式;
(2)画出函数的图象;
(3)从图象上观察,当x取何值时,y随x的增大而增大?当x取何值时,函数有最大值(或最小值)?
8.如图,以边长为1的正方形ABCO的两边OA、OC所在直线为轴建立坐标系,点O为原点.
(1)求以A为顶点,且经过点C的抛物线解析式;
(2)求(1)中的抛物线与对角线OB交于点D的坐标.
9.二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
10.如图所示,在直角坐标系中,函数y=﹣x+1与y(x﹣1)2的图象大致是( )
A. B.
C. D.
11.若二次函数y=x2﹣mx+1的图象的顶点在x轴上,则m的值是( )
A.2 B.﹣2 C.0 D.±2
12.把抛物线y=2(x﹣3)2向左平移2个单位长度得到的抛物线解析式为 ________ .
13.已知二次函数y=3(x﹣1)2的图象上有三点A()、B(2,y2)、C(﹣5,y3),则y1、y2、y3的大小关系为________ .
14.若把抛物线y=a(x﹣4)2向左平移6个单位长度后得到抛物线y=﹣3(x﹣h)2,则a=________ ,h=________ .若抛物线y=a(x﹣4)2的顶点为A,且与y轴交于点B,抛物线y=﹣3(x+2)2的顶点为M,则S△MAB=________.
15.如图①是一张眼镜的照片,两镜片下半部分轮廓可以近似看成抛物线形状.建立如图②直角坐标系,已知左轮廓线端点A、B间的距离为4cm,点A、B与右轮廓线端点D、E均在平行于x轴的直线上,最低点C在x轴上,且与AB的距离CH=1cm,y轴平分BD,BD=2cm.解答下列问题:
(1)求轮廓线ACB的函数解析式;(写出自变量x的取值范围)
(2)由(1)写出右轮廓线DFE对应的函数解析式及自变量x的取值范围.
16.已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
17.如图,直线l:yx+经过点B(,2),且与x轴交于点A,将抛物线C1:yx2沿x轴正方向平移t个单位,记平移后的抛物线为C2,且与直线l交于F点,其顶点为P.
(1)当抛物线C2与直线l交于y轴上同一点时,求t的值;
(2)抛物线C2与y轴交于点E,与直线AB交于两点,其中一个交点为F.当线段EF∥x轴时,求平移后的抛物线C2对应的函数关系式.
【参考答案】
1.A.
2.B.
3.A.
4.向上,x=5,(5,0),右,5,y=2(x+2)2.
5.y.
6.1.
7.(1)∵x=﹣2为抛物线y=a(x﹣h)2的对称轴,
∴抛物线的解析式为:y=a(x+2)2,
将(1,﹣3)代入可得,
﹣3=a(1+2)2,
解得:a,
∴抛物线的解析式为:y(x+2)2;
(2)如图所示,
(3)∵该抛物线的对称轴为:x=﹣2,
∴顶点坐标为(﹣2,0),
根据抛物线的对称性得,当x<﹣2时,y随x的增大而增大,
∵0,
∴函数有最大值,
∴当x=﹣2时,函数有最大值是0.
8.(1)A的坐标是(1,0)、C坐标是(0,1),设出解析式是y=a(x﹣1)2,把C的坐标代入得:a(﹣1)2=1,
解得:a=1,
则抛物线的解析式是:y=(x﹣1)2;
(2)B的坐标是(1,1),
设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x.
根据题意得:,
解得:(舍去),或.
则D的坐标是:(,).
9.(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a,
∴二次函数解析式为y1(x﹣2)2a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:,
解得:k,b=﹣1,
则直线AB解析式为yx﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
10.B.
11.D.
12.y=2(x﹣1)2.
13.y1<y2<y3.
14.﹣3,﹣2,144.
15(1)y2(﹣5≤x≤﹣1);
(2)由左右两轮廓线关于y轴对称,
又y(x+3)2,顶点C(﹣3,0),
∴顶点C关于y轴对称点F(3,0)且a1,
∴右轮廓线DFE对应的函数解析式为y(x﹣3)2,即:yx2x(1≤x≤5).
16.(1)设一次函数解析式为y=kx+b,
把A(4,0),B(0,4)分别代入解析式得,
解得,
解析式为y=﹣x+4.
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴(4﹣1)n=3,
解得,n=2,
把M(m,2)代入为2=﹣m+4得,m=2,
M(2,2),
∵抛物线y=a(x﹣h)2的顶点为P(1,0),
可得y=a(x﹣1)2,
把M(2,2)代入y=a(x﹣1)2得,2=a(2﹣1)2,解得a=2,函数解析式为y=2(x﹣1)2.
17。解:(1)把B(,2)代入yx+b得()+b=2,解得b=3,
∴一次函数解析式为yx+3,
当x=0时,yx+3=3,则一次函数与y轴的交点坐标为(0,3),
yx2沿x轴正方向平移t个单位后所得抛物线解析式为y(x﹣t)2,
把(0,3)代入y(x﹣t)2得t1=3,t2=﹣3(舍去),
即t的值为3;
(2)当x=0时,y(x﹣t)2t2,则E(0,t2)
∵EF∥x轴,
而抛物线y(x﹣t)2的对称轴为直线x=t,
∴F点坐标为(2t,t2)
把F(2t,t2)代入yx+3得 2t+3t2,解得t1=3,t2(舍去),
∴平移后的抛物线C2对应的函数关系式为y(x﹣3)2.
第7页(共7页)
