北师大版七下数学第四章全等三角形典型证明题专练(Word版,附答案解析)
文档属性
| 名称 | 北师大版七下数学第四章全等三角形典型证明题专练(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 356.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 21:55:09 | ||
图片预览


文档简介
全等三角形典型证明题专练
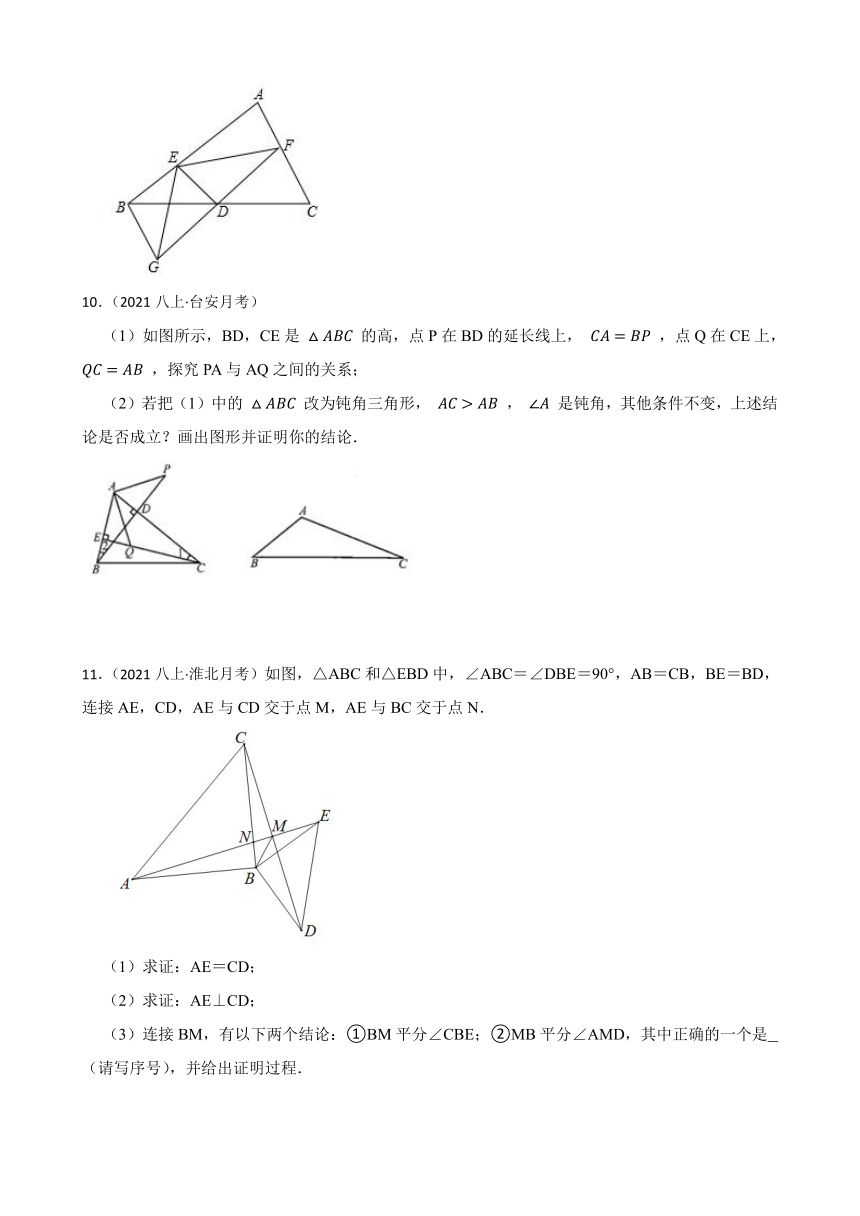
1.(2021八上·南充期末)如图, 是 的中线,F为 上一点,E为 延长线上一点,且 .求证: .
2.(2021八上·营口期末)已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.求证:PC=AN.
3.(2021八上·乌兰察布期末)如图所示,AB//DC,ADCD,BE平分∠ABC,且点E是AD的中点,试探求AB、CD与BC的数量关系,并说明你的理由.
4.(2021八上·盖州月考)如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
5.(2021八上·台安月考)如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
6.(2019八上·海淀期中)已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明
7.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
8.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
9.(2021八上·彭水期末)如图, 中, , 是 上一点,满足 ,连接 交 于点 , ,交 于点 ,连结 .
(1)求证: .
(2)请你判断 与 的大小关系,并证明你的结论.
10.(2021八上·台安月考)
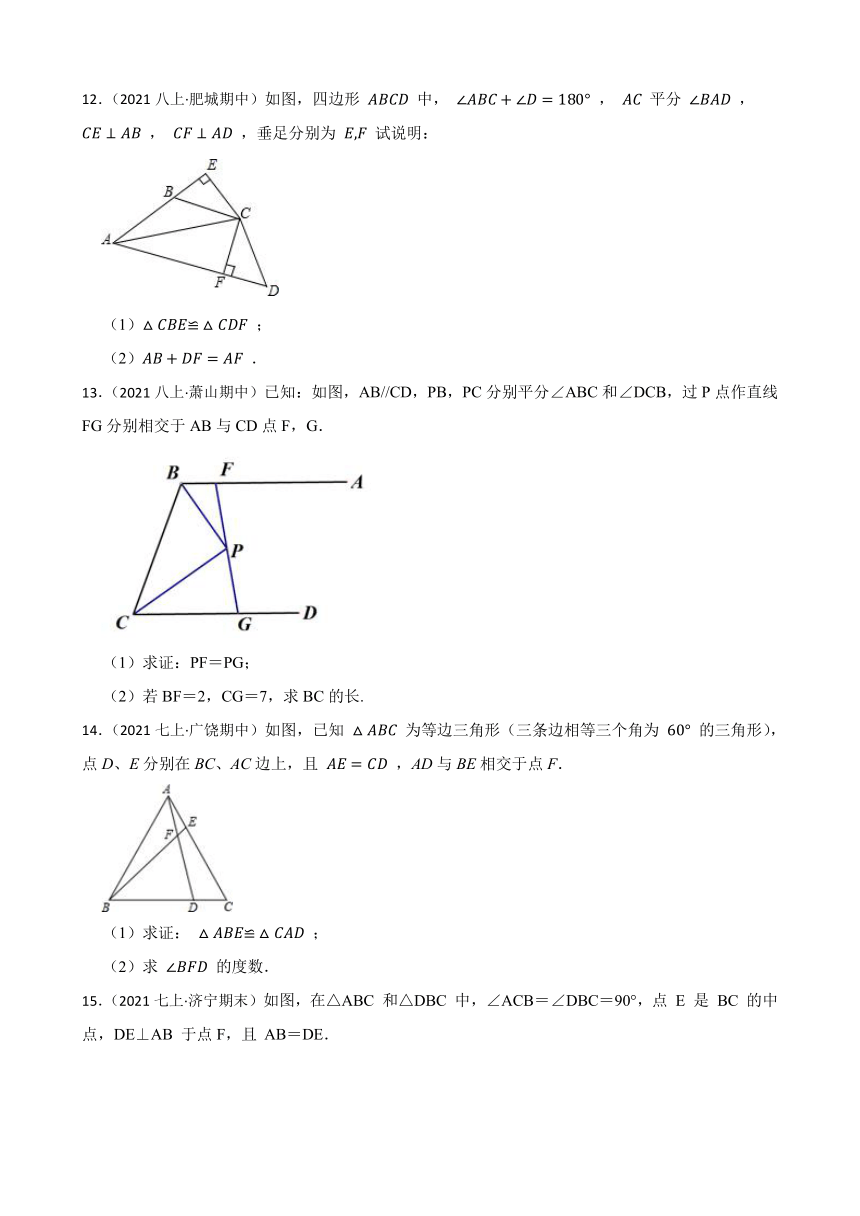
(1)如图所示,BD,CE是 的高,点P在BD的延长线上, ,点Q在CE上, ,探究PA与AQ之间的关系;
(2)若把(1)中的 改为钝角三角形, , 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
11.(2021八上·淮北月考)如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD,其中正确的一个是 (请写序号),并给出证明过程.
12.(2021八上·肥城期中)如图,四边形 中, , 平分 , , ,垂足分别为 试说明:
(1) ;
(2) .
13.(2021八上·萧山期中)已知:如图,AB//CD,PB,PC分别平分∠ABC和∠DCB,过P点作直线FG分别相交于AB与CD点F,G.
(1)求证:PF=PG;
(2)若BF=2,CG=7,求BC的长.
14.(2021七上·广饶期中)如图,已知 为等边三角形(三条边相等三个角为 的三角形),点D、E分别在BC、AC边上,且 ,AD与BE相交于点F.
(1)求证: ;
(2)求 的度数.
15.(2021七上·济宁期末)如图,在△ABC 和△DBC 中,∠ACB=∠DBC=90°,点 E 是 BC 的中点,DE⊥AB 于点F,且 AB=DE.
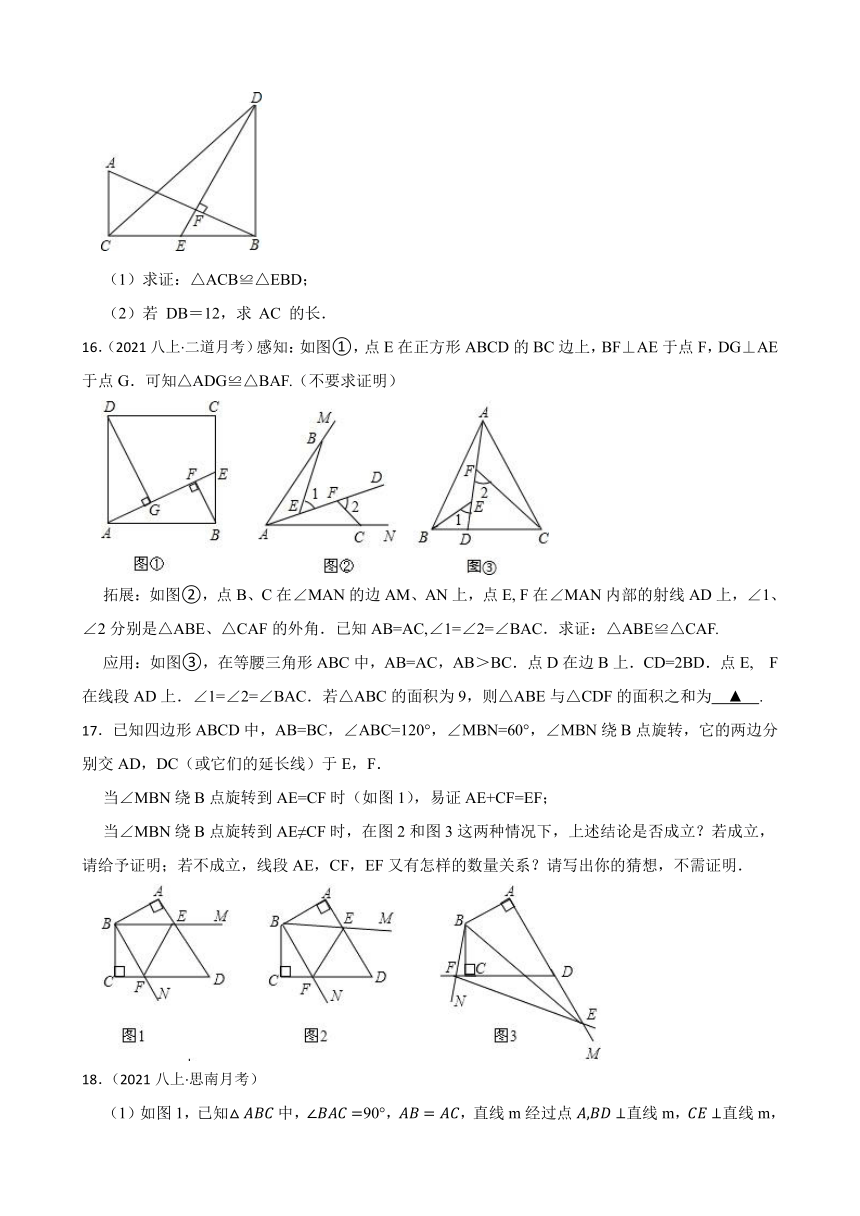
(1)求证:△ACB≌△EBD;
(2)若 DB=12,求 AC 的长.
16.(2021八上·二道月考)感知:如图①,点E在正方形ABCD的BC边上,BF⊥AE于点F,DG⊥AE于点G.可知△ADG≌△BAF.(不要求证明)
拓展:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边B上.CD=2BD.点E, F在线段AD上.∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为 ▲ .
17.已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.
18.(2021八上·思南月考)
(1)如图1,已知中,90°,,直线m经过点直线m,直线m,垂足分别为点.求证:.
(2)如图2,将(1)中的条件改为:在中,三点都在直线m上,并且有.请写出三条线段的数量关系,并说明理由.
19.(2021八上·柯桥月考)在 中, ,点 是 上一点(不与 , 重合),以 为一边
在 的右侧作 ,使 , ,连接 .
(1)如图1,若 ,
①求证; ;
②求 的度数.
(2)设 , .如图2,则 , 之间有怎样的数量关系?请直接写出你的结论.
20.(2021七下·汉台期末)已知:△ABC中,∠ACB=90°,AC=BC,过点A作AD⊥AE,且AE=AD.
(1)如图1,当点D在线段BC上时,过点E作EH⊥AC于H,连接DE.求证:EH=AC:
(2)如图2,当点D在CB延长线上时,连接BE交AC的延长线于点M.求证:BM=EM:
21.(2021八上·东莞期末)如图
(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
22.(2021八上·五常期末)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
23.(2021七下·寿阳期末)综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
24.(2021九下·庆云月考)
(1)问题背景
如图1:在四边形ABCD中,AB=AD, BAD=120°, B= ADC=90°.E,F 分别是 BC,CD上的点.且 EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG.先证明ΔABE≌ΔADG;再证明ΔAEF≌ΔAGF,可得出结论,他的结论应是 ;
请你帮他完成证明过程
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD, B+ D=180°.E,F分别是BC,CD上的点,且 EAF= BAD,上述结论是否仍然成立,并说明理由;
(3)实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(0处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲,乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
答案解析部分
1.【答案】证明: 是 边上的中线,
.
在 和 中,
,
.
.
.
2.【答案】证明:∵,,
∴,
∴,
∴,
∵,,
∴,
在和中,
,
∴,
∵,,
∴,
∵,,,
∴,
∵,,
∴,
∴.
3.【答案】证明:∵AB//DC,ADCD,
∴∠A=∠D=90°,
过点E作EF⊥BC于点F,则∠EFB=∠A=90°,
又∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵BE=BE,
∴△ABE≌△FBE(AAS),
∴AE=EF,AB=BF,
又点E是AD的中点,
∴AE=ED=EF,
∴Rt△CDE≌Rt△CFE(HL),
∴CD=CF,
∴BC=CF+BF=AB+CD.
4.【答案】证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
5.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
6.【答案】解:猜想:EF=2AD,EF⊥AD.
证明:如图,延长AD到M,使得AD=DM,连接MC,延长DA交EF于N,
∴AD=DM,AM=2AD,
∵AD是△ABC的中线,∴BD=CD,
在△ABD和△MCD中,
, ∴△ABD≌△MCD(SAS),
∴AB=MC,∠BAD=∠M,
∵AB=AE,∴AE=MC,
∵AE⊥AB,AF⊥AC,∴∠EAB=∠FAC=90°,
∵∠FAC+∠BAC+∠EAB+∠EAF=360°,∴∠BAC+∠EAF=180°,
∵∠CAD+∠M+∠MCA=180°,∴∠CAD+∠BAD+∠MCA=180°,
即∠BAC+∠MCA=180°,∴∠EAF=∠MCA.
在△AEF和△CMA中,
,∴△AEF≌△CMA(SAS),
∴EF=AM,∠CAM=∠F,∴EF=2AD;
∵∠CAF=90°,∴∠CAM+∠FAN=90°,
∵∠CAM=∠F,∴∠F+∠FAN=90°,
∴∠ANF=90°,∴EF⊥AD.
7.【答案】证明:在AB上截取AF=AD,
∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵ ,
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵ ,
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
8.【答案】(1)解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)解:FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD
又∵AF为公共边
在△EAF和△GAF中
∵AE=AG,∠EAF=∠FAG,AF=AF,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵∠DFC=∠GFC,FC=FC,∠FCG=∠FCD,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
9.【答案】(1)证明:∵ ,
∴
在 和 中,
∴
∴
(2)解:
理由如下:
∵
∴
又∵
∴
在 和 中
∴
∴在 中, 即 .
10.【答案】(1)解:∵ ,
∴ , .
∴ .
在 和 中,
∴ .
∴ , .
∵ ,
∴
∴
即 .
∴ .
即 , .
(2)解:上述结论仍然成立.如图所示
∵ , ,
∴ , .
∵ ,
∴ .
在 和 中,
∴ .
∴ , .
∵ ,
∴ .
∴ .
∴ .
∴ ,
即 , .
11.【答案】(1)解:∠ABC=∠DBE=90°,
,
即,
,
(SAS),
(2)解:
,BE=BD,
(3)②
12.【答案】(1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D
在△CBE与△CDF中,
,
∴△CBE≌△CDF;
(2)在Rt△ACE与Rt△ACF中,
,
∴△ACE≌△ACF
∴AE=AF
∴AB+DF=AB+BE=AE=AF.
13.【答案】(1)证明: 延长BP交CD于点M
∵AB//CD
∴∠ABC+∠BCD=180°,∠FBP=∠GMP
∵BP平分∠ABC
∴∠CBP= ∠ABC
同理,∠BCP= ∠BCD
∴∠CBP+∠BCP= (∠ABC+∠BCD)=90°
∴∠BPC=180°-(∠CBP+∠BCP)=90°
∴∠CPM=180°-∠BPC=90°=∠BPC
∵CP平分∠DCB
∴∠BCP=∠MCP
∴∠CBP=∠CMP
∴BC=MC
∴BP=MP
∵∠BPF=∠MPG
∴△BPF≌△MPG(ASA)
∴PF=PG
(2)解:∵△BPF≌△MPG
∴GM=BF=2
∴MC=CG+GM=7+2=9
∴BC=MC=9
14.【答案】(1)解:∵ 为等边三角形,
∴ , .
在 和 中,
,
∴ (SAS);
(2)∵ ,
∴ .
∵ ,
∴ .
15.【答案】(1)解:,,
,
,
在和中,,
;
(2)解:由(1)已证:,
,
点是的中点,
,
.
16.【答案】解:拓展:证明:如图②
∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3.∴∠4=∠ABE.
∵∠AEB=∠AFC,∠ABE=∠4,AB=AC,
∴△ABE≌△CAF(AAS);应用:6
17.【答案】解:∵AB⊥AD,BC⊥CD,AB=BC,AE=CF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS);
∴∠ABE=∠CBF,BE=BF;
∵∠ABC=120°,∠MBN=60°,
∴∠ABE=∠CBF=30°,
∴AE= BE,CF= BF;
∵∠MBN=60°,BE=BF,
∴△BEF为等边三角形;
∴AE+CF= BE+ BF=BE=EF;
图2成立,图3不成立.
证明图2.
延长DC至点K,使CK=AE,连接BK,
在△BAE和△BCK中,
则△BAE≌△BCK,
∴BE=BK,∠ABE=∠KBC,
∵∠FBE=60°,∠ABC=120°,
∴∠FBC+∠ABE=60°,
∴∠FBC+∠KBC=60°,
∴∠KBF=∠FBE=60°,
在△KBF和△EBF中,
∴△KBF≌△EBF,
∴KF=EF,
∴KC+CF=EF,
即AE+CF=EF.
图3不成立,
AE、CF、EF的关系是AE﹣CF=EF.
18.【答案】(1)证明:如图1,∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD;
(2)解:,理由如下:
如图2,∵∠BDA=∠AEC=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴BD+CE=AE+AD=DE;
19.【答案】(1)解:① ,
.即 .
在 与 中,
,
;
② ,
.即 .
在 与 中,
,
,
.
,
,
又
;
(2)解: ,
20.【答案】(1)证明:∵AD⊥AE,EH⊥AC,
∴∠AHE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠EAH=∠ADC,
又∵AD=AE,∠ACD=∠AHE=90°,
∴△AHE≌△DCA(AAS),
∴EH=AC;
(2)解:如图2,过点E作EN⊥AM,交AM的延长线于N,
∵AD⊥AE,EN⊥AM,
∴∠ANE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAN=90°,
∴∠EAN=∠ADC,
又∵AD=AE,∠ACD=∠ANE=90°,
∴△ANE≌△DCA(AAS),
∴EN=AC,
∵BC=AC,
∴BC=NE,
又∵∠BMC=∠EMN,∠BCM=∠ENM=90°,
∴△BCM≌△ENM(AAS),
∴BM=EM.
21.【答案】(1)EF=BE+FD
(2)解:(1)中的结论仍然成立,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF=∠BAD,
∴∠2+∠4=∠EAF,
∴∠EAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
(3)解:(1)中的结论不成立,EF=BE﹣FD,
理由如下:如图3,在EB上截取BH=DF,连接AH,
同(2)中证法可得,△ABH≌△ADF,
∴AH=AF,∠BAH=∠DAF,
∴∠HAE=∠FAE,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∵EH=BE﹣BH=BE﹣DF,
∴EF=BE﹣FD.
22.【答案】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
∴△AEC≌△CGB,
∴AE=CG
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
在△BCE和△CAM中,
∴△BCE≌△CAM,
∴BE=CM.
23.【答案】(1)证明:如图1中,
,
,
,
, ,
.
(2)结论: 符合题意.
理由:如图2中,
平分 , ,
,
,
,
,
在 和 中,
,
,
.
(3)结论: .
理由: 是 的中点,
,
在 和 中,
,
.
24.【答案】(1)解:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
(2)解:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF= ∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD-∠EAF,
=∠BAD- ∠BAD= ∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
(3)解:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°= ∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
1.(2021八上·南充期末)如图, 是 的中线,F为 上一点,E为 延长线上一点,且 .求证: .
2.(2021八上·营口期末)已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.求证:PC=AN.
3.(2021八上·乌兰察布期末)如图所示,AB//DC,ADCD,BE平分∠ABC,且点E是AD的中点,试探求AB、CD与BC的数量关系,并说明你的理由.
4.(2021八上·盖州月考)如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
5.(2021八上·台安月考)如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
6.(2019八上·海淀期中)已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明
7.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
8.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
9.(2021八上·彭水期末)如图, 中, , 是 上一点,满足 ,连接 交 于点 , ,交 于点 ,连结 .
(1)求证: .
(2)请你判断 与 的大小关系,并证明你的结论.
10.(2021八上·台安月考)
(1)如图所示,BD,CE是 的高,点P在BD的延长线上, ,点Q在CE上, ,探究PA与AQ之间的关系;
(2)若把(1)中的 改为钝角三角形, , 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
11.(2021八上·淮北月考)如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD,其中正确的一个是 (请写序号),并给出证明过程.
12.(2021八上·肥城期中)如图,四边形 中, , 平分 , , ,垂足分别为 试说明:
(1) ;
(2) .
13.(2021八上·萧山期中)已知:如图,AB//CD,PB,PC分别平分∠ABC和∠DCB,过P点作直线FG分别相交于AB与CD点F,G.
(1)求证:PF=PG;
(2)若BF=2,CG=7,求BC的长.
14.(2021七上·广饶期中)如图,已知 为等边三角形(三条边相等三个角为 的三角形),点D、E分别在BC、AC边上,且 ,AD与BE相交于点F.
(1)求证: ;
(2)求 的度数.
15.(2021七上·济宁期末)如图,在△ABC 和△DBC 中,∠ACB=∠DBC=90°,点 E 是 BC 的中点,DE⊥AB 于点F,且 AB=DE.
(1)求证:△ACB≌△EBD;
(2)若 DB=12,求 AC 的长.
16.(2021八上·二道月考)感知:如图①,点E在正方形ABCD的BC边上,BF⊥AE于点F,DG⊥AE于点G.可知△ADG≌△BAF.(不要求证明)
拓展:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边B上.CD=2BD.点E, F在线段AD上.∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为 ▲ .
17.已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.
18.(2021八上·思南月考)
(1)如图1,已知中,90°,,直线m经过点直线m,直线m,垂足分别为点.求证:.
(2)如图2,将(1)中的条件改为:在中,三点都在直线m上,并且有.请写出三条线段的数量关系,并说明理由.
19.(2021八上·柯桥月考)在 中, ,点 是 上一点(不与 , 重合),以 为一边
在 的右侧作 ,使 , ,连接 .
(1)如图1,若 ,
①求证; ;
②求 的度数.
(2)设 , .如图2,则 , 之间有怎样的数量关系?请直接写出你的结论.
20.(2021七下·汉台期末)已知:△ABC中,∠ACB=90°,AC=BC,过点A作AD⊥AE,且AE=AD.
(1)如图1,当点D在线段BC上时,过点E作EH⊥AC于H,连接DE.求证:EH=AC:
(2)如图2,当点D在CB延长线上时,连接BE交AC的延长线于点M.求证:BM=EM:
21.(2021八上·东莞期末)如图
(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
22.(2021八上·五常期末)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
23.(2021七下·寿阳期末)综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
24.(2021九下·庆云月考)
(1)问题背景
如图1:在四边形ABCD中,AB=AD, BAD=120°, B= ADC=90°.E,F 分别是 BC,CD上的点.且 EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG.先证明ΔABE≌ΔADG;再证明ΔAEF≌ΔAGF,可得出结论,他的结论应是 ;
请你帮他完成证明过程
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD, B+ D=180°.E,F分别是BC,CD上的点,且 EAF= BAD,上述结论是否仍然成立,并说明理由;
(3)实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(0处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲,乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
答案解析部分
1.【答案】证明: 是 边上的中线,
.
在 和 中,
,
.
.
.
2.【答案】证明:∵,,
∴,
∴,
∴,
∵,,
∴,
在和中,
,
∴,
∵,,
∴,
∵,,,
∴,
∵,,
∴,
∴.
3.【答案】证明:∵AB//DC,ADCD,
∴∠A=∠D=90°,
过点E作EF⊥BC于点F,则∠EFB=∠A=90°,
又∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵BE=BE,
∴△ABE≌△FBE(AAS),
∴AE=EF,AB=BF,
又点E是AD的中点,
∴AE=ED=EF,
∴Rt△CDE≌Rt△CFE(HL),
∴CD=CF,
∴BC=CF+BF=AB+CD.
4.【答案】证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
5.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
6.【答案】解:猜想:EF=2AD,EF⊥AD.
证明:如图,延长AD到M,使得AD=DM,连接MC,延长DA交EF于N,
∴AD=DM,AM=2AD,
∵AD是△ABC的中线,∴BD=CD,
在△ABD和△MCD中,
, ∴△ABD≌△MCD(SAS),
∴AB=MC,∠BAD=∠M,
∵AB=AE,∴AE=MC,
∵AE⊥AB,AF⊥AC,∴∠EAB=∠FAC=90°,
∵∠FAC+∠BAC+∠EAB+∠EAF=360°,∴∠BAC+∠EAF=180°,
∵∠CAD+∠M+∠MCA=180°,∴∠CAD+∠BAD+∠MCA=180°,
即∠BAC+∠MCA=180°,∴∠EAF=∠MCA.
在△AEF和△CMA中,
,∴△AEF≌△CMA(SAS),
∴EF=AM,∠CAM=∠F,∴EF=2AD;
∵∠CAF=90°,∴∠CAM+∠FAN=90°,
∵∠CAM=∠F,∴∠F+∠FAN=90°,
∴∠ANF=90°,∴EF⊥AD.
7.【答案】证明:在AB上截取AF=AD,
∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵ ,
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵ ,
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
8.【答案】(1)解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)解:FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD
又∵AF为公共边
在△EAF和△GAF中
∵AE=AG,∠EAF=∠FAG,AF=AF,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵∠DFC=∠GFC,FC=FC,∠FCG=∠FCD,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
9.【答案】(1)证明:∵ ,
∴
在 和 中,
∴
∴
(2)解:
理由如下:
∵
∴
又∵
∴
在 和 中
∴
∴在 中, 即 .
10.【答案】(1)解:∵ ,
∴ , .
∴ .
在 和 中,
∴ .
∴ , .
∵ ,
∴
∴
即 .
∴ .
即 , .
(2)解:上述结论仍然成立.如图所示
∵ , ,
∴ , .
∵ ,
∴ .
在 和 中,
∴ .
∴ , .
∵ ,
∴ .
∴ .
∴ .
∴ ,
即 , .
11.【答案】(1)解:∠ABC=∠DBE=90°,
,
即,
,
(SAS),
(2)解:
,BE=BD,
(3)②
12.【答案】(1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D
在△CBE与△CDF中,
,
∴△CBE≌△CDF;
(2)在Rt△ACE与Rt△ACF中,
,
∴△ACE≌△ACF
∴AE=AF
∴AB+DF=AB+BE=AE=AF.
13.【答案】(1)证明: 延长BP交CD于点M
∵AB//CD
∴∠ABC+∠BCD=180°,∠FBP=∠GMP
∵BP平分∠ABC
∴∠CBP= ∠ABC
同理,∠BCP= ∠BCD
∴∠CBP+∠BCP= (∠ABC+∠BCD)=90°
∴∠BPC=180°-(∠CBP+∠BCP)=90°
∴∠CPM=180°-∠BPC=90°=∠BPC
∵CP平分∠DCB
∴∠BCP=∠MCP
∴∠CBP=∠CMP
∴BC=MC
∴BP=MP
∵∠BPF=∠MPG
∴△BPF≌△MPG(ASA)
∴PF=PG
(2)解:∵△BPF≌△MPG
∴GM=BF=2
∴MC=CG+GM=7+2=9
∴BC=MC=9
14.【答案】(1)解:∵ 为等边三角形,
∴ , .
在 和 中,
,
∴ (SAS);
(2)∵ ,
∴ .
∵ ,
∴ .
15.【答案】(1)解:,,
,
,
在和中,,
;
(2)解:由(1)已证:,
,
点是的中点,
,
.
16.【答案】解:拓展:证明:如图②
∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3.∴∠4=∠ABE.
∵∠AEB=∠AFC,∠ABE=∠4,AB=AC,
∴△ABE≌△CAF(AAS);应用:6
17.【答案】解:∵AB⊥AD,BC⊥CD,AB=BC,AE=CF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS);
∴∠ABE=∠CBF,BE=BF;
∵∠ABC=120°,∠MBN=60°,
∴∠ABE=∠CBF=30°,
∴AE= BE,CF= BF;
∵∠MBN=60°,BE=BF,
∴△BEF为等边三角形;
∴AE+CF= BE+ BF=BE=EF;
图2成立,图3不成立.
证明图2.
延长DC至点K,使CK=AE,连接BK,
在△BAE和△BCK中,
则△BAE≌△BCK,
∴BE=BK,∠ABE=∠KBC,
∵∠FBE=60°,∠ABC=120°,
∴∠FBC+∠ABE=60°,
∴∠FBC+∠KBC=60°,
∴∠KBF=∠FBE=60°,
在△KBF和△EBF中,
∴△KBF≌△EBF,
∴KF=EF,
∴KC+CF=EF,
即AE+CF=EF.
图3不成立,
AE、CF、EF的关系是AE﹣CF=EF.
18.【答案】(1)证明:如图1,∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD;
(2)解:,理由如下:
如图2,∵∠BDA=∠AEC=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴BD+CE=AE+AD=DE;
19.【答案】(1)解:① ,
.即 .
在 与 中,
,
;
② ,
.即 .
在 与 中,
,
,
.
,
,
又
;
(2)解: ,
20.【答案】(1)证明:∵AD⊥AE,EH⊥AC,
∴∠AHE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠EAH=∠ADC,
又∵AD=AE,∠ACD=∠AHE=90°,
∴△AHE≌△DCA(AAS),
∴EH=AC;
(2)解:如图2,过点E作EN⊥AM,交AM的延长线于N,
∵AD⊥AE,EN⊥AM,
∴∠ANE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAN=90°,
∴∠EAN=∠ADC,
又∵AD=AE,∠ACD=∠ANE=90°,
∴△ANE≌△DCA(AAS),
∴EN=AC,
∵BC=AC,
∴BC=NE,
又∵∠BMC=∠EMN,∠BCM=∠ENM=90°,
∴△BCM≌△ENM(AAS),
∴BM=EM.
21.【答案】(1)EF=BE+FD
(2)解:(1)中的结论仍然成立,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF=∠BAD,
∴∠2+∠4=∠EAF,
∴∠EAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
(3)解:(1)中的结论不成立,EF=BE﹣FD,
理由如下:如图3,在EB上截取BH=DF,连接AH,
同(2)中证法可得,△ABH≌△ADF,
∴AH=AF,∠BAH=∠DAF,
∴∠HAE=∠FAE,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∵EH=BE﹣BH=BE﹣DF,
∴EF=BE﹣FD.
22.【答案】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
∴△AEC≌△CGB,
∴AE=CG
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
在△BCE和△CAM中,
∴△BCE≌△CAM,
∴BE=CM.
23.【答案】(1)证明:如图1中,
,
,
,
, ,
.
(2)结论: 符合题意.
理由:如图2中,
平分 , ,
,
,
,
,
在 和 中,
,
,
.
(3)结论: .
理由: 是 的中点,
,
在 和 中,
,
.
24.【答案】(1)解:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
(2)解:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF= ∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD-∠EAF,
=∠BAD- ∠BAD= ∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
(3)解:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°= ∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
