北师大版八年级数学下册 6.4 多边形的内角和课件 (共15张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.4 多边形的内角和课件 (共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 07:47:28 | ||
图片预览






文档简介
(共15张PPT)
方法1:测量法。
北师大版八年级下册
§ 6.4 多边形内角和
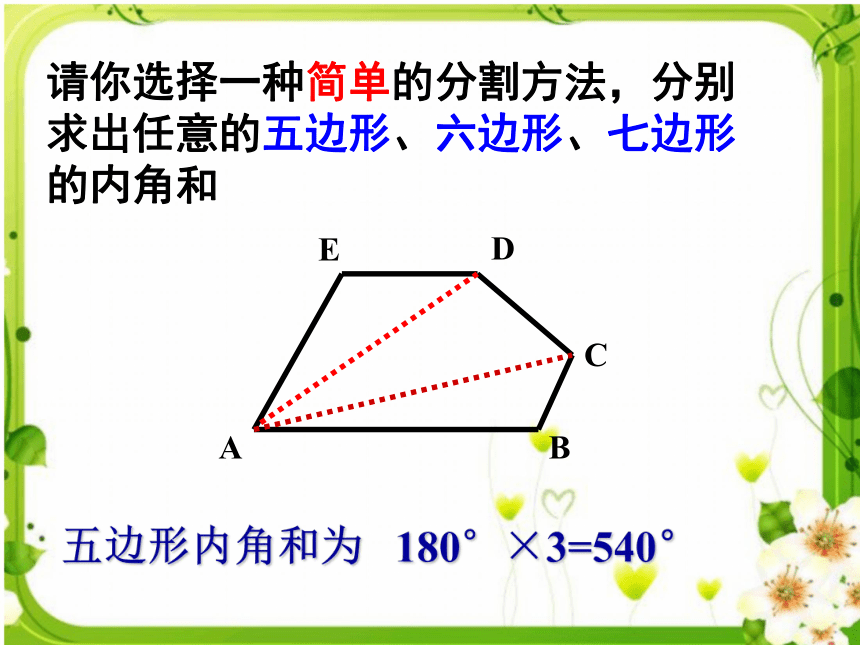
学习目标1.你已经知道哪些图形的内角和2.利用三角形内角和求解多边形内角和。3.思考哪些方法可以帮助我们解决这类规律性问题。三角形的内角和等于度.长方形的内角和等于度.正方形的内角和等于度.ABCABCDABCD方法2:拼图法方法1:测量法2413241324132413任意四边形的内角和等于多少度呢?你是怎样得到的?你能找到几种方法?方法3:分割法四边形内角和为:360°)24(180°=-×小结方法综合这几种方法,其共同点是什么 从一个顶点出发和各顶点相连,把四边形的问题转化为三角形的问题。转化思想请你选择一种简单的分割方法,分别求出任意的五边形、六边形、七边形的内角和ABCDE五边形内角和为180°×3=540°任意六边形内角和、七边形内角和FDCBAECDEFBAG六边形内角和为:180°×4=720°七边形内角和为:180°×5=900°3×180°-180°=360°4×180°-360°=360°方法1:方法2:方法3:方法4:2×180°=360°3×180°-180°=360°
点在外部
点在内部
点在边上
点在角上
(n-2)×180°
(n-1)×180°-180°
n×180°-360°
(n-1)×180°-180°
(n-2)×180°
n边形的内角和等于多少度呢?
多边形的内角和定理:
归纳:n边形的内角和等于
(n-2)·180
强调指出:① n≥3的正整数
②n边形的内角和是180的整数倍。
③多边形内角和只与边数有关,与
多边形的大小,形状无关
应用新知 尝试练习
1、七边形内角和为 。
2、多边形内角和为 ,则它是 边形。
3、求右侧图形中 的值:
5、一个多边形的各个内角都等于120°,它是几边形?
6、四边形的四个内角∠A、∠B、∠C、∠D的度数之比为5∶5∶3∶5,求它的四个内角的度数.
拓展提升
一个矩形纸片剪去一个角后,所得的多边形的内角和是多少?
本节课你学到了什么?
课后作业
A组(必做题):
(1)一个多边形的内角和等于900°,则这个多边形的边数 为 。
(2)已知八边形的各个内角相等,则每个内角都等于 。
(3)如果一个多边形的每一个外角都等于30°,则这个多边形的边数是_____。
(4)n边形的边数每增加一条,那么它的内角和就增加( )
A、360° B、180° C、90° D、240°
B组(选做题):
在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
方法1:测量法。
北师大版八年级下册
§ 6.4 多边形内角和
学习目标1.你已经知道哪些图形的内角和2.利用三角形内角和求解多边形内角和。3.思考哪些方法可以帮助我们解决这类规律性问题。三角形的内角和等于度.长方形的内角和等于度.正方形的内角和等于度.ABCABCDABCD方法2:拼图法方法1:测量法2413241324132413任意四边形的内角和等于多少度呢?你是怎样得到的?你能找到几种方法?方法3:分割法四边形内角和为:360°)24(180°=-×小结方法综合这几种方法,其共同点是什么 从一个顶点出发和各顶点相连,把四边形的问题转化为三角形的问题。转化思想请你选择一种简单的分割方法,分别求出任意的五边形、六边形、七边形的内角和ABCDE五边形内角和为180°×3=540°任意六边形内角和、七边形内角和FDCBAECDEFBAG六边形内角和为:180°×4=720°七边形内角和为:180°×5=900°3×180°-180°=360°4×180°-360°=360°方法1:方法2:方法3:方法4:2×180°=360°3×180°-180°=360°
点在外部
点在内部
点在边上
点在角上
(n-2)×180°
(n-1)×180°-180°
n×180°-360°
(n-1)×180°-180°
(n-2)×180°
n边形的内角和等于多少度呢?
多边形的内角和定理:
归纳:n边形的内角和等于
(n-2)·180
强调指出:① n≥3的正整数
②n边形的内角和是180的整数倍。
③多边形内角和只与边数有关,与
多边形的大小,形状无关
应用新知 尝试练习
1、七边形内角和为 。
2、多边形内角和为 ,则它是 边形。
3、求右侧图形中 的值:
5、一个多边形的各个内角都等于120°,它是几边形?
6、四边形的四个内角∠A、∠B、∠C、∠D的度数之比为5∶5∶3∶5,求它的四个内角的度数.
拓展提升
一个矩形纸片剪去一个角后,所得的多边形的内角和是多少?
本节课你学到了什么?
课后作业
A组(必做题):
(1)一个多边形的内角和等于900°,则这个多边形的边数 为 。
(2)已知八边形的各个内角相等,则每个内角都等于 。
(3)如果一个多边形的每一个外角都等于30°,则这个多边形的边数是_____。
(4)n边形的边数每增加一条,那么它的内角和就增加( )
A、360° B、180° C、90° D、240°
B组(选做题):
在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
