苏科版七年级数学下册 第7章 平面图形的认识(二)小结与思考 课件(共27张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 第7章 平面图形的认识(二)小结与思考 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 09:58:35 | ||
图片预览



文档简介
(共27张PPT)
小结与思考
平行线的判定与性质
平行线的判定
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
(数----形)
(形----数)
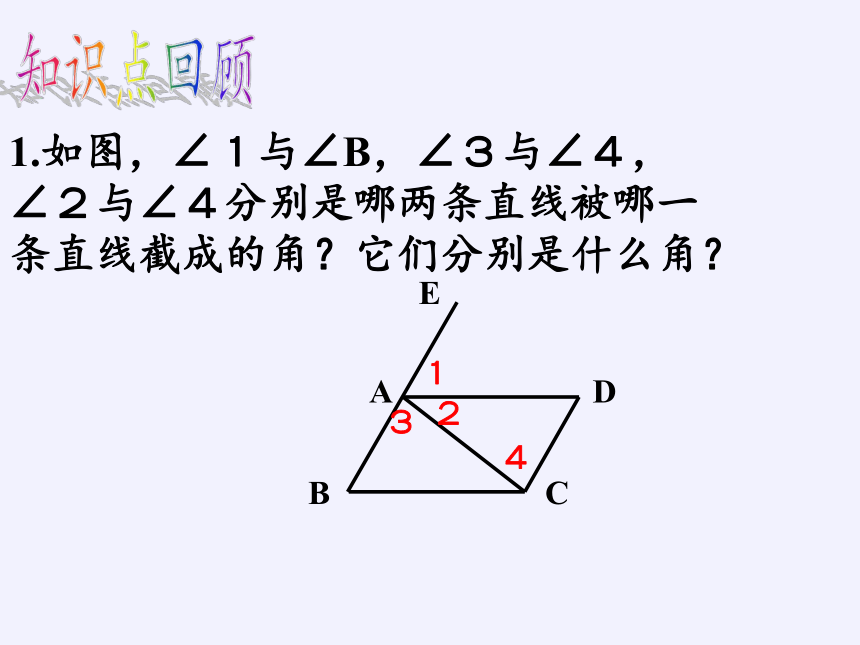
1.如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
1
2
3
4
A
B
C
D
E
知识点回顾
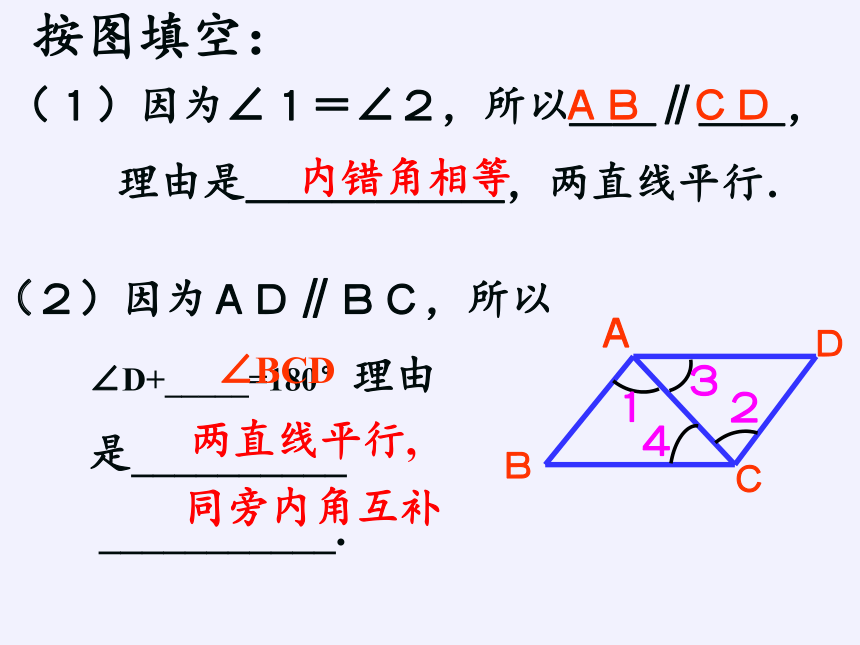
(1)因为∠1=∠2,所以__∥__,
理由是______,两直线平行.
A
B
C
D
1
2
3
4
AB CD
内错角相等
(2)因为AD∥BC,所以
∠D+_____=180°理由
是__________
___________.
两直线平行,
同旁内角互补
∠BCD
按图填空:
例题学习
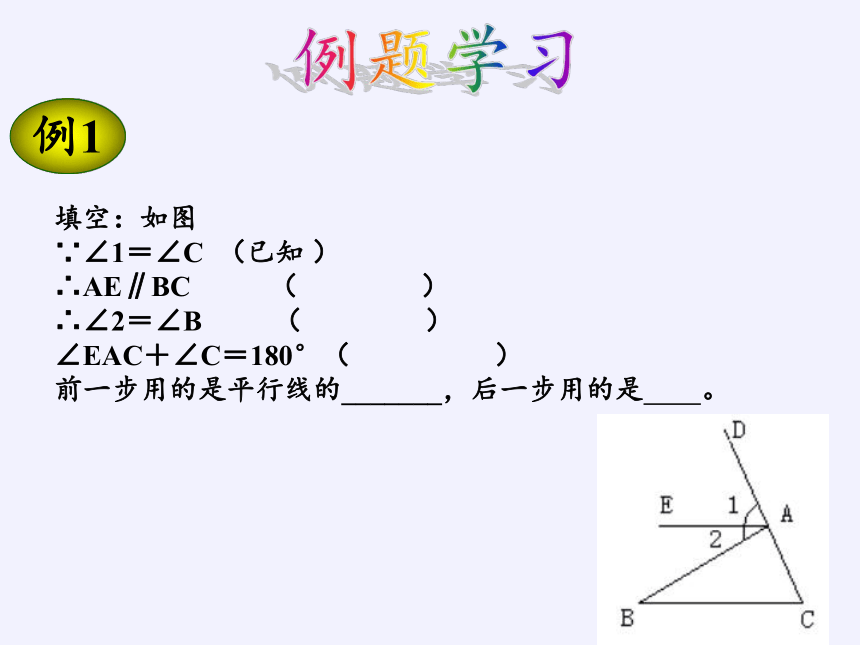
例1
填空:如图
∵∠1=∠C (已知 )
∴AE∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
下列说法中,不正确的是( )
A.两条平行直线被第三条直线所截,平行线的内错角的平分线互相平行
B.两条平行直线被第三条直线所截,平行线的同位角的平分线互相平行
C.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相平行
D.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相垂直
例2
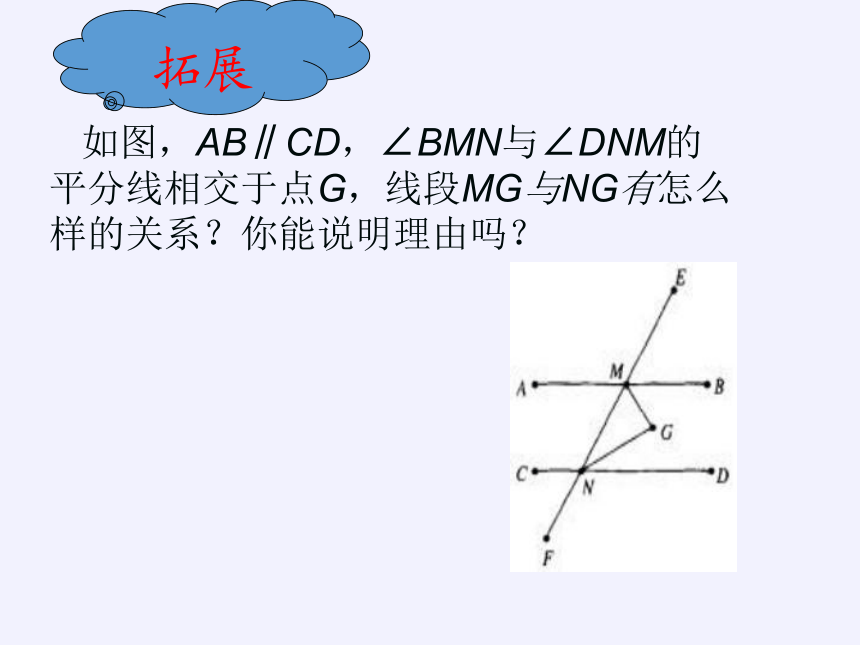
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,线段MG与NG有怎么样的关系?你能说明理由吗?
拓展
课堂练习
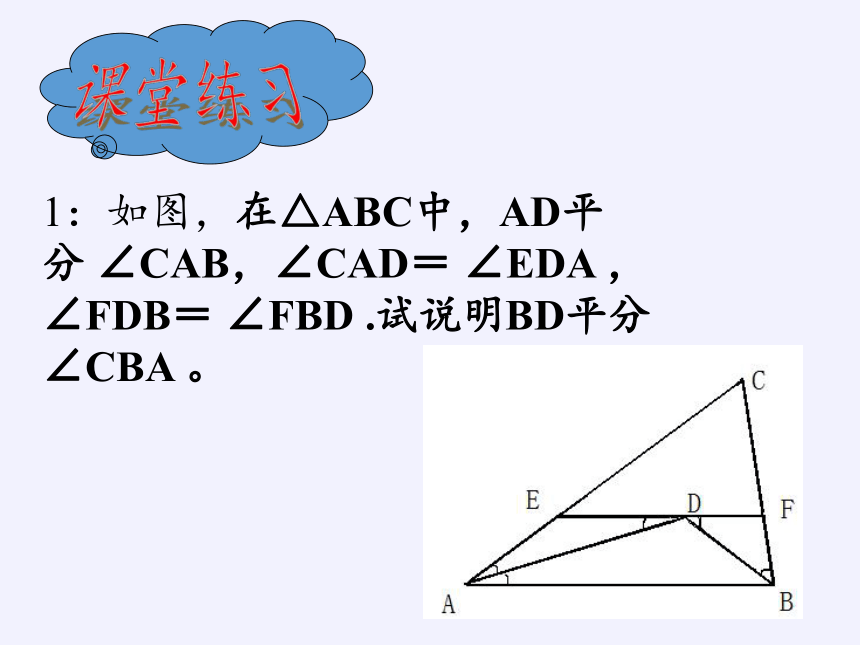
1:如图,在△ABC中,AD平分 ∠CAB,∠CAD= ∠EDA , ∠FDB= ∠FBD .试说明BD平分∠CBA 。
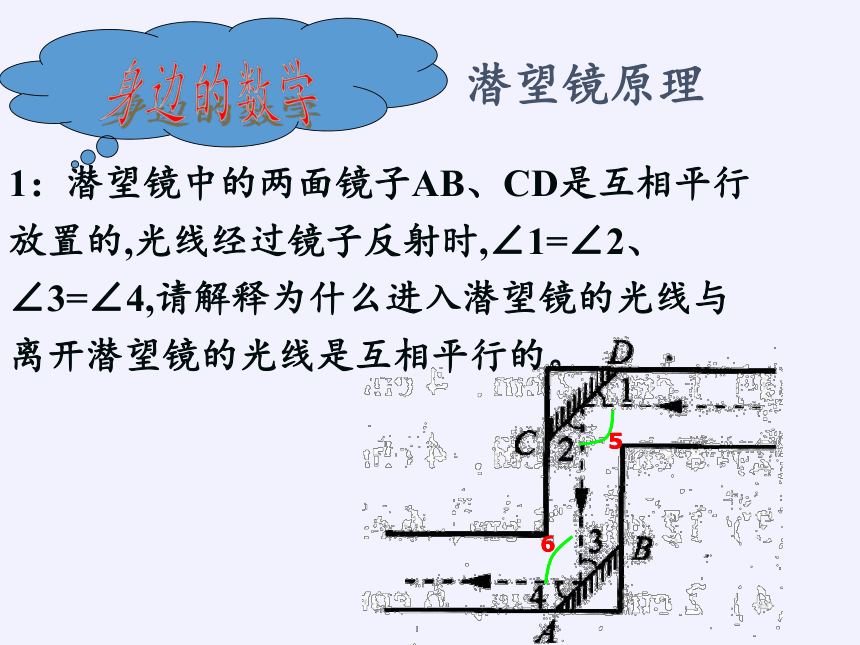
1:潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
5
6
身边的数学
潜望镜原理
5
6
5
6
潜望镜小知识
作用:处于水下航行状态的潜艇观察海平面和空中情况的唯一手段便是借助潜望镜。而多数潜艇均安装有两部潜望镜――一部攻击潜望镜和一部观察潜望镜。前者用于发现和瞄准水面目标,而后者主要用于观察海空情况和导航观测。潜艇在浮出水面前,艇长都必须指挥潜艇在潜望镜深度先用潜望镜对海平面作一次360度的观察,以求尽早发现可能出现的敌情。只有在确认没有任何威胁的情况下潜艇才会浮出水面。
缺陷:潜望镜升至指挥塔外5米高的位置,两端都安装有棱镜和透镜并可将潜望镜的视野放大至1X到6X。潜望镜的使用有两个很明显的问题:当潜望镜完全升起时,细长的潜望镜桅杆会影响潜艇的正常航行,造成横向的不稳定。另外一个重要问题是潜望镜镜片产生的雾气。由于潜艇内部空气潮湿,潜望镜的镜片多会产生雾气,所以潜望镜在设计制造时就必须尽量做到防水和密封。
2:如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠1、∠2的度数。
身边的数学
身边的数学
3:如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿GF折叠成图3,则图3中的∠CFE的度数是 °
大家一起来
如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
合作探究
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
例4:(1)如图1,△ABC中∠ABC与∠ACB的平分线相交于点P.试探索∠BPC与∠A的数量关系。
1
2
例题学习
图1
见课本36页
例题学习
(2)如图2,点P是△ABC中两外角∠DBC与∠ECB平分线的交点.试探索∠BPC与∠A的数量关系.
图2
1
2
见课本36页
(3)如图3,点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点。试探索∠BPC与∠A的数量关系。
图3
1
2
例题学习
见课本36页
A
B
如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗 为什么
练习3:解答题:
·
D
E
F
1
2
3
4
c
·
13.已知如图∠xOy=900,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围。
例题学习
例5
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
课堂练习
1
在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东60,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
0
课堂练习
2
如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=150,应怎样确定点E的位置?为什么?
0
E
课堂练习
3
如图,∠1=∠2,∠3=100,则∠4=
0
课堂练习
4
如图,EG∥AB,FG∥DC,∠B=100,
∠C =120,则 ∠EGF =
0
0
100
0
120
0
80
0
60
0
课堂练习
5
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
F
1
2
课堂练习
拓展
如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
1
2
谢 谢
小结与思考
平行线的判定与性质
平行线的判定
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
(数----形)
(形----数)
1.如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
1
2
3
4
A
B
C
D
E
知识点回顾
(1)因为∠1=∠2,所以__∥__,
理由是______,两直线平行.
A
B
C
D
1
2
3
4
AB CD
内错角相等
(2)因为AD∥BC,所以
∠D+_____=180°理由
是__________
___________.
两直线平行,
同旁内角互补
∠BCD
按图填空:
例题学习
例1
填空:如图
∵∠1=∠C (已知 )
∴AE∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
下列说法中,不正确的是( )
A.两条平行直线被第三条直线所截,平行线的内错角的平分线互相平行
B.两条平行直线被第三条直线所截,平行线的同位角的平分线互相平行
C.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相平行
D.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相垂直
例2
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,线段MG与NG有怎么样的关系?你能说明理由吗?
拓展
课堂练习
1:如图,在△ABC中,AD平分 ∠CAB,∠CAD= ∠EDA , ∠FDB= ∠FBD .试说明BD平分∠CBA 。
1:潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
5
6
身边的数学
潜望镜原理
5
6
5
6
潜望镜小知识
作用:处于水下航行状态的潜艇观察海平面和空中情况的唯一手段便是借助潜望镜。而多数潜艇均安装有两部潜望镜――一部攻击潜望镜和一部观察潜望镜。前者用于发现和瞄准水面目标,而后者主要用于观察海空情况和导航观测。潜艇在浮出水面前,艇长都必须指挥潜艇在潜望镜深度先用潜望镜对海平面作一次360度的观察,以求尽早发现可能出现的敌情。只有在确认没有任何威胁的情况下潜艇才会浮出水面。
缺陷:潜望镜升至指挥塔外5米高的位置,两端都安装有棱镜和透镜并可将潜望镜的视野放大至1X到6X。潜望镜的使用有两个很明显的问题:当潜望镜完全升起时,细长的潜望镜桅杆会影响潜艇的正常航行,造成横向的不稳定。另外一个重要问题是潜望镜镜片产生的雾气。由于潜艇内部空气潮湿,潜望镜的镜片多会产生雾气,所以潜望镜在设计制造时就必须尽量做到防水和密封。
2:如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠1、∠2的度数。
身边的数学
身边的数学
3:如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿GF折叠成图3,则图3中的∠CFE的度数是 °
大家一起来
如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
合作探究
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
例4:(1)如图1,△ABC中∠ABC与∠ACB的平分线相交于点P.试探索∠BPC与∠A的数量关系。
1
2
例题学习
图1
见课本36页
例题学习
(2)如图2,点P是△ABC中两外角∠DBC与∠ECB平分线的交点.试探索∠BPC与∠A的数量关系.
图2
1
2
见课本36页
(3)如图3,点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点。试探索∠BPC与∠A的数量关系。
图3
1
2
例题学习
见课本36页
A
B
如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗 为什么
练习3:解答题:
·
D
E
F
1
2
3
4
c
·
13.已知如图∠xOy=900,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围。
例题学习
例5
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
课堂练习
1
在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东60,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
0
课堂练习
2
如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=150,应怎样确定点E的位置?为什么?
0
E
课堂练习
3
如图,∠1=∠2,∠3=100,则∠4=
0
课堂练习
4
如图,EG∥AB,FG∥DC,∠B=100,
∠C =120,则 ∠EGF =
0
0
100
0
120
0
80
0
60
0
课堂练习
5
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
F
1
2
课堂练习
拓展
如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
1
2
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
