2021-2022学年华东师大版七年级数学下册 第6章 一元一次方程 单元测试 (word含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学下册 第6章 一元一次方程 单元测试 (word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 12:25:43 | ||
图片预览


文档简介
华东师大版八年级数学下册
第6章 一元一次方程
单元测试训练卷
一、选择题(共10小题,每小题4分,共40分)
1. 如果x2-2n-1=0是关于x的一元一次方程,那么n的值为( )
A.0 B.1 C. D.
2. 下列等式变形正确的是( )
A.若a=b,则a-3=3-b
B.若x=y,则=
C.若a=b,则ac=bc
D.若=,则b=d
3. 把方程=1-去分母后,正确的结果是( )
A.2x-1=1-(3-x)
B.2(2x-1)=1-(3-x)
C.2(2x-1)=8-3-x
D.2(2x-1)=8-3+x
4. 下列方程中,解是2的方程是( )
A.x=2 B.-x+=0
C.3x+6=0 D.5-3x=1
5. 若a,b互为相反数(a≠0),则关于x的方程ax+b=0的解是( )
A.x=1 B.x=-1
C.x=1或x=-1 D.不能确定
6. 关于x的方程(|m|-1)x2+(m-1)x+7m2=0是一元一次方程,则( )
A.m=0 B.m=-1
C.m=±1 D.m≠1
7. 小马虎在计算16-x时,不慎将“-”看成了“+”,计算的结果是17,那么正确的计算结果应该是( )
A.15 B.13 C.7 D.-1
8. 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32 Cm,则小长方形的面积是( )
A.8 Cm2 B.10 Cm2
C.12 Cm2 D.16 Cm2
9. 某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A.22+x=2×26
B.22+x=2(26-x)
C.2(22+x)=26-x
D.22=2(26-x)
10. 甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%.那么顾客到哪家超市购买这种商品更合算( )
A.甲 B.乙 C.丙 D.一样
二.填空题(共6小题,每小题4分,共24分)
11. 已知方程3-2xa-3=7是关于x的一元一次方程,则a=__ _.
12. 若(a-1)x|a|=3是关于x的一元一次方程,则a=________.
13. 已知y=3是方程ay=-6的解,那么关于x的方程4(x-a)=a-(x-6)的解是________.
14. 一个水池有甲、乙两个进水管,单独开甲水管2 h注满全池,单独开乙水管3 h注满全池,如果同时开放两个水管,则注满水池需要__ __.
15. 某种商品每件的进价为210元,按标价的8折销售时,利润率为15%,设这种商品的标价为每件x元,根据题意列方程为__ __.
16. 如图,是由六块正方形拼成的一个长方形.已知最小的正方形面积为1,则长方形的面积是__ _.
三.解答题(共6小题, 56分)
17.(6分) 解方程:
(1)2(x+1)=x-(2x-5);
(2)x+=3.
18.(8分) )当x取何值时,代数式的值比代数式x-4的值小1
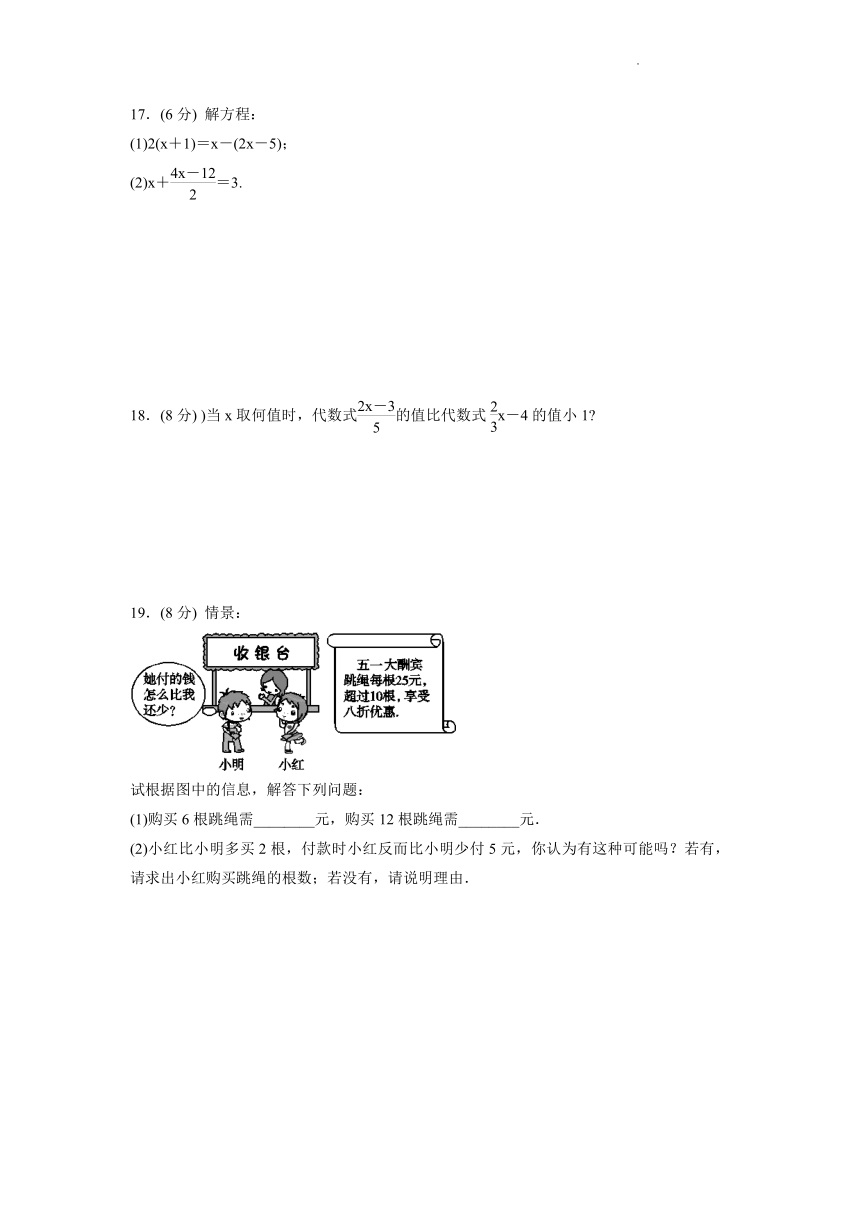
19.(8分) 情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需________元,购买12根跳绳需________元.
(2)小红比小明多买2根,付款时小红反而比小明少付5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
20.(10分) 整理一批图书,若由一个人独做需要80个小时完成,假设每人的工作效率相同.
(1)若限定32小时完成,一个人先做8小时,再需增加多少人帮忙才能在规定的时间内完成?
(2)计划由一部分人先做4小时,然后增加3人与他们一起做4小时,正好完成这项工作的,应该安排多少人先工作?
21.(12分) 阅读以下例题:解方程:|3x|=1.
解:①当3x>0时,方程化为3x=1,∴x=.②当3x<0时,方程化为-3x=1,∴x=-,∴原方程的解为x=或x=-.
根据上面的方法,解下列方程:
(1)|x-3|=2;
(2)|2x+1|=5.
22.(12分) 某店用500元购进甲、乙两件商品,然后将甲、乙两件商品分别按50%和40%的利润标定售价.
(1)如果按上述进价和售价进行交易,那么该店买卖这两件商品能否盈利260元?为什么?
(2)如果该店按原定售价的八折促销,某顾客同时购买了甲、乙两件商品,实际付款584元,
参考答案
1-5CCDBA 6-10BACBC
11. 4
12.-1
13.x=-
14.h
15.0.8x-210=210×0.15
16.143
17. 解:(1)2(x+1)=x-(2x-5), 2x+2 =x-2x+5,2x-x+2x=5-2, 3x=3, x=1.
(2)x+=3,2x+4x-12=6,2x+4x=6+12,x=18,x=3.
18. 解:根据题意得:+1=x-4,去分母,得6x-9+15=10x-60,移项合并,得4x=66,解得x=.
19. 解:(1)150,240
(2)有这种可能.设小红购买跳绳x根,则小明购买跳绳(x-2)根,则根据题意可列出方程:25×80%·x=25(x-2)-5.解得x=11.因此小红购买跳绳11根.
20. 解:(1)设再需增加x人帮忙才能在规定的时间内完成,可得: +=1,解得:x=2.答:再需增加2人帮忙才能在规定的时间内完成.
(2)设应该安排x人先工作,可得: +=,解得:x=6.答:应该安排6人先工作.
21. 解:(1) 当x>3时, |x-3|=x-3∴x-3=2,x=5
当x=3时,|x-3|=0,0=2∴舍去
当x<3时,|x-3|=3-x∴3-x=2∴x=1
(2)当2x>-1时,|2x+1|=2x+1∴2x+1=5∴x=2
当2x=-1时,|2x+1|=0,0=5不成立 舍去
当2x<-1时,|2x+1|=-2x-1∴-2x-1=5,x=-3
22. 解:(1)不能.∵500×50%=250(元),250<260,∴该店买卖这两件商品不能盈利260元.那么甲、乙两件商品的进价各是多少元?
(2)设甲商品的进价为x元,则乙商品的进价为(500-x)元,依题意得80%×[(1+50%)x+(1+40%)(500-x)]=584,解得x=300,∴500-x=200.答:甲商品的进价为300元,乙商品的进价为200元.
第6章 一元一次方程
单元测试训练卷
一、选择题(共10小题,每小题4分,共40分)
1. 如果x2-2n-1=0是关于x的一元一次方程,那么n的值为( )
A.0 B.1 C. D.
2. 下列等式变形正确的是( )
A.若a=b,则a-3=3-b
B.若x=y,则=
C.若a=b,则ac=bc
D.若=,则b=d
3. 把方程=1-去分母后,正确的结果是( )
A.2x-1=1-(3-x)
B.2(2x-1)=1-(3-x)
C.2(2x-1)=8-3-x
D.2(2x-1)=8-3+x
4. 下列方程中,解是2的方程是( )
A.x=2 B.-x+=0
C.3x+6=0 D.5-3x=1
5. 若a,b互为相反数(a≠0),则关于x的方程ax+b=0的解是( )
A.x=1 B.x=-1
C.x=1或x=-1 D.不能确定
6. 关于x的方程(|m|-1)x2+(m-1)x+7m2=0是一元一次方程,则( )
A.m=0 B.m=-1
C.m=±1 D.m≠1
7. 小马虎在计算16-x时,不慎将“-”看成了“+”,计算的结果是17,那么正确的计算结果应该是( )
A.15 B.13 C.7 D.-1
8. 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32 Cm,则小长方形的面积是( )
A.8 Cm2 B.10 Cm2
C.12 Cm2 D.16 Cm2
9. 某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A.22+x=2×26
B.22+x=2(26-x)
C.2(22+x)=26-x
D.22=2(26-x)
10. 甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%.那么顾客到哪家超市购买这种商品更合算( )
A.甲 B.乙 C.丙 D.一样
二.填空题(共6小题,每小题4分,共24分)
11. 已知方程3-2xa-3=7是关于x的一元一次方程,则a=__ _.
12. 若(a-1)x|a|=3是关于x的一元一次方程,则a=________.
13. 已知y=3是方程ay=-6的解,那么关于x的方程4(x-a)=a-(x-6)的解是________.
14. 一个水池有甲、乙两个进水管,单独开甲水管2 h注满全池,单独开乙水管3 h注满全池,如果同时开放两个水管,则注满水池需要__ __.
15. 某种商品每件的进价为210元,按标价的8折销售时,利润率为15%,设这种商品的标价为每件x元,根据题意列方程为__ __.
16. 如图,是由六块正方形拼成的一个长方形.已知最小的正方形面积为1,则长方形的面积是__ _.
三.解答题(共6小题, 56分)
17.(6分) 解方程:
(1)2(x+1)=x-(2x-5);
(2)x+=3.
18.(8分) )当x取何值时,代数式的值比代数式x-4的值小1
19.(8分) 情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需________元,购买12根跳绳需________元.
(2)小红比小明多买2根,付款时小红反而比小明少付5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
20.(10分) 整理一批图书,若由一个人独做需要80个小时完成,假设每人的工作效率相同.
(1)若限定32小时完成,一个人先做8小时,再需增加多少人帮忙才能在规定的时间内完成?
(2)计划由一部分人先做4小时,然后增加3人与他们一起做4小时,正好完成这项工作的,应该安排多少人先工作?
21.(12分) 阅读以下例题:解方程:|3x|=1.
解:①当3x>0时,方程化为3x=1,∴x=.②当3x<0时,方程化为-3x=1,∴x=-,∴原方程的解为x=或x=-.
根据上面的方法,解下列方程:
(1)|x-3|=2;
(2)|2x+1|=5.
22.(12分) 某店用500元购进甲、乙两件商品,然后将甲、乙两件商品分别按50%和40%的利润标定售价.
(1)如果按上述进价和售价进行交易,那么该店买卖这两件商品能否盈利260元?为什么?
(2)如果该店按原定售价的八折促销,某顾客同时购买了甲、乙两件商品,实际付款584元,
参考答案
1-5CCDBA 6-10BACBC
11. 4
12.-1
13.x=-
14.h
15.0.8x-210=210×0.15
16.143
17. 解:(1)2(x+1)=x-(2x-5), 2x+2 =x-2x+5,2x-x+2x=5-2, 3x=3, x=1.
(2)x+=3,2x+4x-12=6,2x+4x=6+12,x=18,x=3.
18. 解:根据题意得:+1=x-4,去分母,得6x-9+15=10x-60,移项合并,得4x=66,解得x=.
19. 解:(1)150,240
(2)有这种可能.设小红购买跳绳x根,则小明购买跳绳(x-2)根,则根据题意可列出方程:25×80%·x=25(x-2)-5.解得x=11.因此小红购买跳绳11根.
20. 解:(1)设再需增加x人帮忙才能在规定的时间内完成,可得: +=1,解得:x=2.答:再需增加2人帮忙才能在规定的时间内完成.
(2)设应该安排x人先工作,可得: +=,解得:x=6.答:应该安排6人先工作.
21. 解:(1) 当x>3时, |x-3|=x-3∴x-3=2,x=5
当x=3时,|x-3|=0,0=2∴舍去
当x<3时,|x-3|=3-x∴3-x=2∴x=1
(2)当2x>-1时,|2x+1|=2x+1∴2x+1=5∴x=2
当2x=-1时,|2x+1|=0,0=5不成立 舍去
当2x<-1时,|2x+1|=-2x-1∴-2x-1=5,x=-3
22. 解:(1)不能.∵500×50%=250(元),250<260,∴该店买卖这两件商品不能盈利260元.那么甲、乙两件商品的进价各是多少元?
(2)设甲商品的进价为x元,则乙商品的进价为(500-x)元,依题意得80%×[(1+50%)x+(1+40%)(500-x)]=584,解得x=300,∴500-x=200.答:甲商品的进价为300元,乙商品的进价为200元.
