2021-2022学年苏科版九年级下册数学6.7用相似三角形解决问题同步测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级下册数学6.7用相似三角形解决问题同步测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 269.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 11:49:22 | ||
图片预览

文档简介
6.7用相似三角形解决问题 同步测试
一.选择题
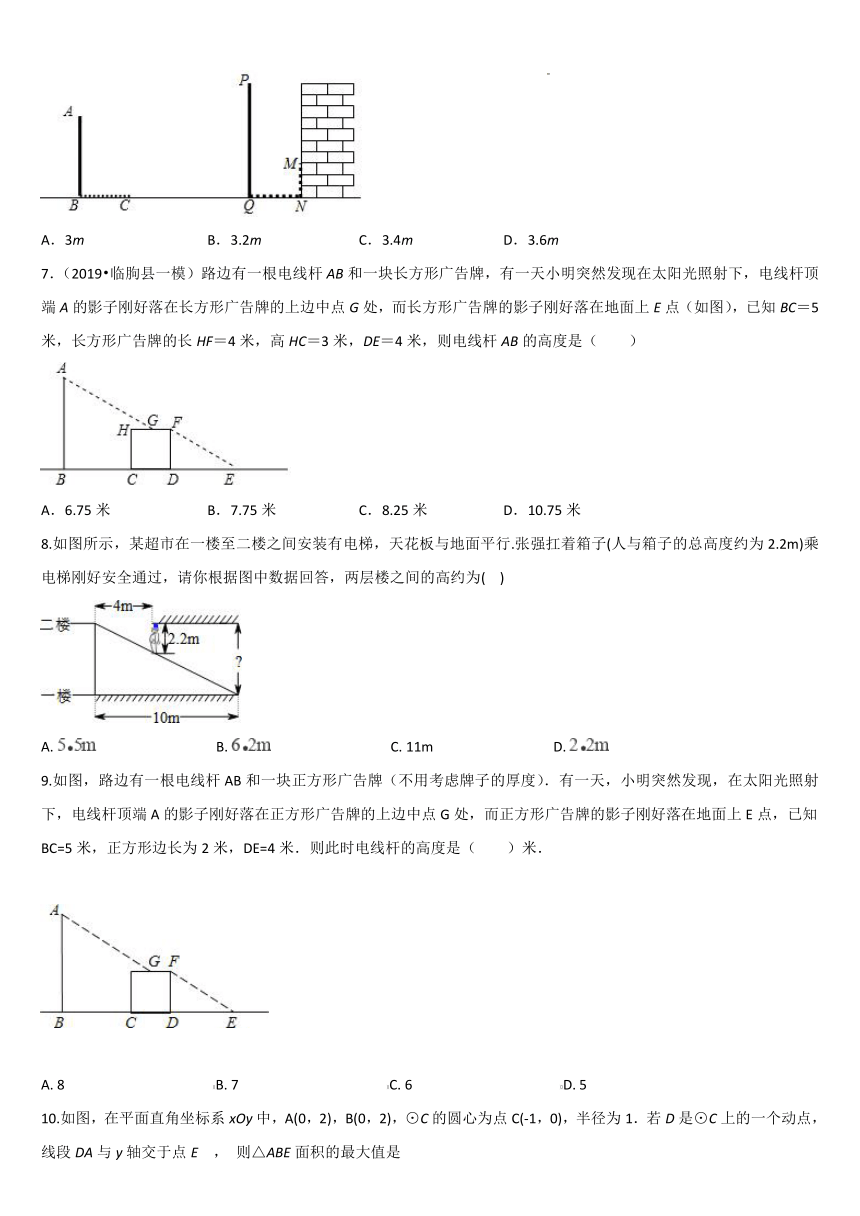
1.有一块直角边AB=4cm,BC=3cm,∠B=90°的Rt△ABC的铁片,现要按照如图所示方式截一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
2. 下列投影中属于中心投影的是( )
A.阳光下跑动的运动员的影子 B.阳光下木杆的影子
C.阳光下汽车的影子 D.路灯下行人的影子
3.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有杆不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
4.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为( )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
5.如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,
长臂外端B升高( )
A.2m B.4m C.4.5m D.8m
6.(2020春 工业园区期末)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为( )
A.3m B.3.2m C.3.4m D.3.6m
7.(2019 临朐县一模)路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
8.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
A. B. C. 11m D.
9.如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.
A. 8 B. 7 C. 6 D. 5
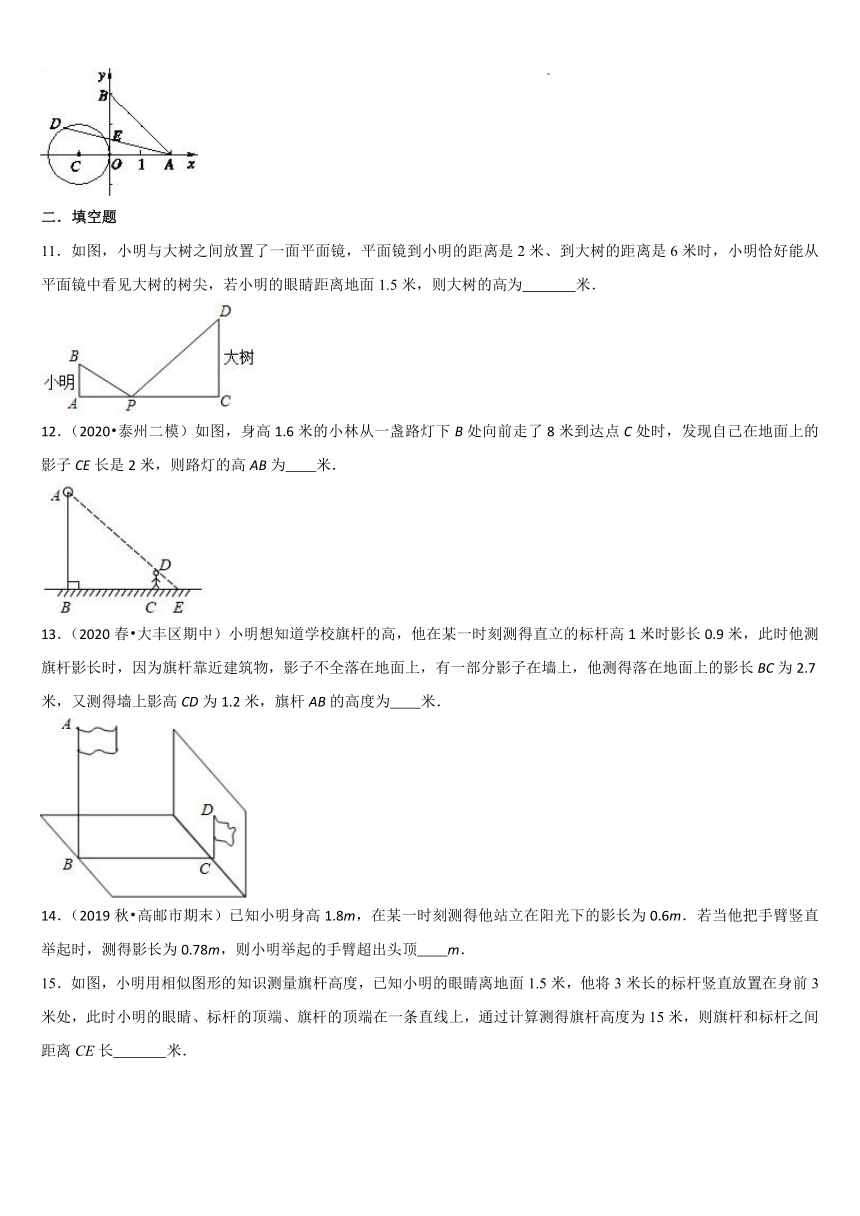
10.如图,在平面直角坐标系xOy中,A(0,2),B(0,2),⊙C的圆心为点C(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E , 则△ABE面积的最大值是
二.填空题
11.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
12.(2020 泰州二模)如图,身高1.6米的小林从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
13.(2020春 大丰区期中)小明想知道学校旗杆的高,他在某一时刻测得直立的标杆高1米时影长0.9米,此时他测旗杆影长时,因为旗杆靠近建筑物,影子不全落在地面上,有一部分影子在墙上,他测得落在地面上的影长BC为2.7米,又测得墙上影高CD为1.2米,旗杆AB的高度为 米.
14.(2019秋 高邮市期末)已知小明身高1.8m,在某一时刻测得他站立在阳光下的影长为0.6m.若当他把手臂竖直举起时,测得影长为0.78m,则小明举起的手臂超出头顶 m.
15.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆高度为15米,则旗杆和标杆之间距离CE长 米.
三.解答题
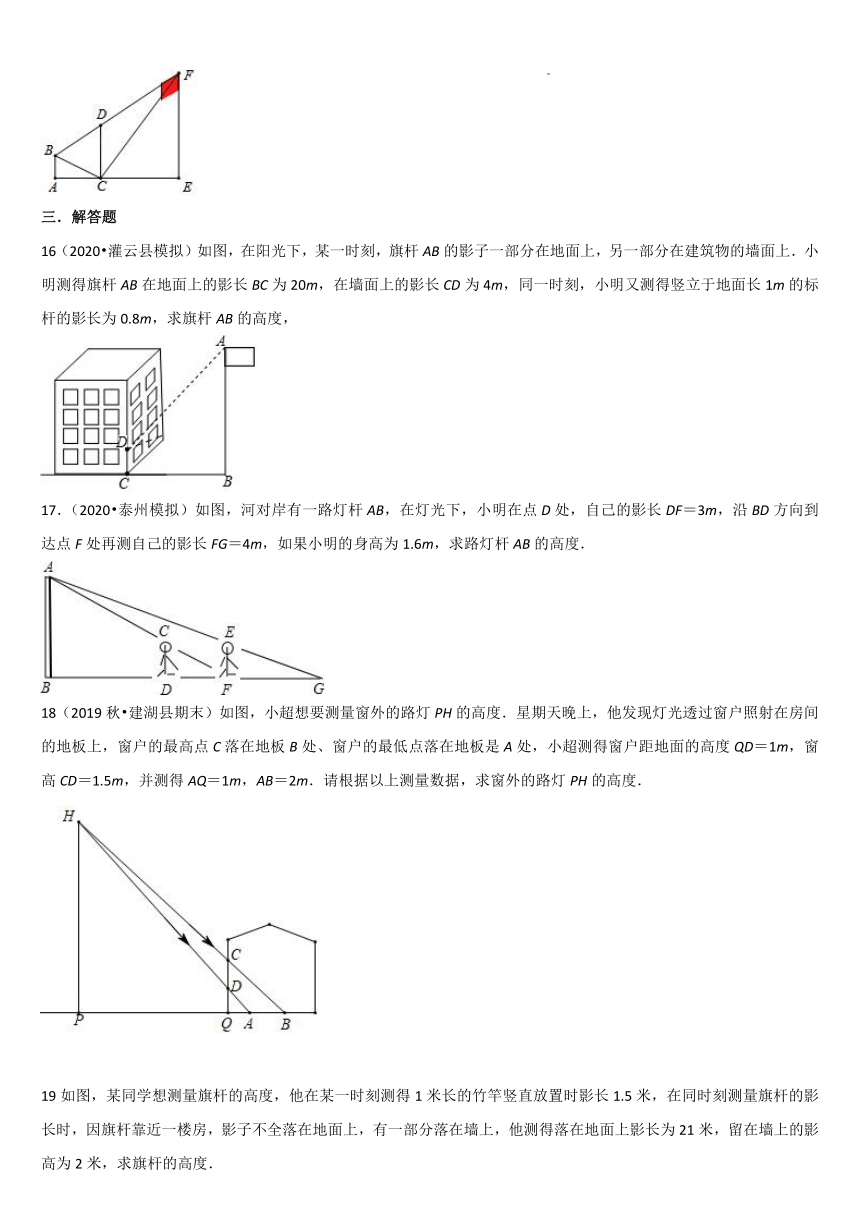
16(2020 灌云县模拟)如图,在阳光下,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为20m,在墙面上的影长CD为4m,同一时刻,小明又测得竖立于地面长1m的标杆的影长为0.8m,求旗杆AB的高度,
17.(2020 泰州模拟)如图,河对岸有一路灯杆AB,在灯光下,小明在点D处,自己的影长DF=3m,沿BD方向到达点F处再测自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
18(2019秋 建湖县期末)如图,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C落在地板B处、窗户的最低点落在地板是A处,小超测得窗户距地面的高度QD=1m,窗高CD=1.5m,并测得AQ=1m,AB=2m.请根据以上测量数据,求窗外的路灯PH的高度.
19如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
20.李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在C点(如图所示),人在F点正好在镜中看到树尖A;第二次他把镜子放在 处,人在 处正好看到树尖A.已知李师傅眼睛距地面的高度为 ,量得 为 , 为 , 为 ,求树高.
21学习了相似三角形的知识后,爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度,并作出了示意图:如图,路灯(点P)距地面若干米,身高1.6米的小明站在距路灯的底部(O点)20米的A点时,身影的长度AM为5米;
(1)请帮助小明求出路灯距地面的高度;
(2)若另一名身高为1.5米小龙站在直线OA上的C点时,测得他与小明的距离AC为7米,求小龙的身影的长度.
参考答案
一.选择题
1.解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC= AB BC= AC BP,
∴BP=.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴.
设DE=x,则有:,
解得x=,
故选:D.
2.
【答案】
D
【解答】
解:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有选项得到的投影为中心投影.
故选:.
3.答案为:B
4.答案为:C
5.答案为:B.
6.(2020春 工业园区期末)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为( )
A.3m B.3.2m C.3.4m D.3.6m
【分析】直接利用同一时刻物体影子与实际高度成比例,进而得出答案.
【解析】连接AC,过点M作MF⊥PF,
∵同一时刻物体影子与实际高度成比例,
∴,
解得:PF=2.4,
∴PQ=PF+FQ=PF+MN=2.4+0.8=3.2(m),
故选:B.
7.(2019 临朐县一模)路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
【分析】过点G作GQ⊥BE于点Q,GP⊥AB于点P,可得四边形BQGP是矩形,然后且△APG与△FDE相似,然后根据相似三角形对应边成比例列式求出AP的长度,再加上CH即可.
【解析】过点G作GQ⊥BE于点Q,GP⊥AB于点P,
根据题意,四边形BQGP是矩形,
∴BP=GQ=3米,
△APG∽△FDE,
∴,
∴AP,
∴AB3=8.25(米),
故选:C.
8.【答案】 A
解:如图,作DE⊥FC于点E,
∴△ABC∽△CED,∴ .
设AB=x米,由题意得DE=6米,EF=2.2米.∴ ,解得x=5.5.故答案为:A.
9.【答案】 D
解:过点G作GH∥BC , GM⊥BE ,
根据题意,四边形BMGH是矩形,
∴BH=GM=2米,
△AHG∽△FDE ,
∴ = ,
∴AH=3,
∴AB=2+3=5米.
故选D .
10.【答案】 D
【解析】
【解答】若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
Rt△ACD中,CD=1,AC=OC+OA=3;
由勾股定理,得:AD=2;
∴S△ACD=AD CD=;
易证得△AOE∽△ADC,
∴=()2=()2=,
即S△AOE=S△ADC=;
∴S△ABE=S△AOB-S△AOE=×2×2-=2-;
故选D.
二.填空题
11.解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴AB=4.5(米),
故答案为:4.5.
12.(2020 泰州二模)如图,身高1.6米的小林从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 8 米.
【分析】根据CD∥AB,得出△ECD∽△EBA,进而得出比例式求出即可.
【解析】由题意知,CE=2米,CD=1.6米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴,即,
解得AB=8(米),
即路灯的高AB为8米;
故答案为:8米.
13.(2020春 大丰区期中)小明想知道学校旗杆的高,他在某一时刻测得直立的标杆高1米时影长0.9米,此时他测旗杆影长时,因为旗杆靠近建筑物,影子不全落在地面上,有一部分影子在墙上,他测得落在地面上的影长BC为2.7米,又测得墙上影高CD为1.2米,旗杆AB的高度为 4.2 米.
【分析】过点D作DE⊥AB于点E,则BE=CD=1.2m,再根据同一时刻物高与影长成正比求出AE的长,进而可得出结论.
【解析】过点D作DE⊥AB于点E,则BE=CD=1.2m,
∵他在某一时刻测得直立的标杆高1米时影长0.9米,
∴,即,
解得:AE=3m,
∴AB=AE+BE=3+1.2=4.2(m).
故答案为:4.2.
14.(2019秋 高邮市期末)已知小明身高1.8m,在某一时刻测得他站立在阳光下的影长为0.6m.若当他把手臂竖直举起时,测得影长为0.78m,则小明举起的手臂超出头顶 0.54 m.
【分析】根据在同一时物体的高度和影长成正比,设出手臂竖直举起时总高度x,即可列方程解出x的值,再减去身高即可得出小明举起的手臂超出头顶的高度.
【解析】设手臂竖直举起时总高度xm,列方程得:,
解得x=2.34,
2.34﹣1.8=0.54m,
所以小明举起的手臂超出头顶的高度为0.54m.
故答案为:0.54.
15.解:如图,延长FB交EA的延长线于T,设TA=x米,EC=y米.
由题意,AB=1.5米,AC=CD=3米,EF=15米.
∵AB∥CD,
∴△TAB∽△TCD,
∴=,
∴=,
解得x=3,
经检验x=3是分式方程的解,
∵CD∥EF,
∴△TCD∽△TEF,
∴=,
∴=,
∴y=24,
经检验y=24是分式方程的解,
∴EC=24(米),
故答案为:24.
三.解答题
16.(2020 灌云县模拟)如图,在阳光下,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为20m,在墙面上的影长CD为4m,同一时刻,小明又测得竖立于地面长1m的标杆的影长为0.8m,求旗杆AB的高度,
【分析】作DE⊥AB于E,可得矩形BCDE,利用同一时刻物高与影长的比一定得到AE的长度,加上CD的长度即为旗杆的高度.
【解析】作DE⊥AB于E,
∵DC⊥BC于C,AB⊥BC于B,
∴四边形BCDE为矩形,
∴DE=BC=20m,BE=DC=4m,
∵同一时刻物高与影长所组成的三角形相似,
∴,
解得AE=25m,
∴AB=25+4=29m.
答:旗杆的高度为29m.
17.(2020 泰州模拟)如图,河对岸有一路灯杆AB,在灯光下,小明在点D处,自己的影长DF=3m,沿BD方向到达点F处再测自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
【分析】在同一时刻物高和影长成正比,根据相似三角形的性质即可解答.
【解析】∵CD∥EF∥AB,
∴可以得到△CDF∽△ABF,△ABG∽△EFG,
∴,,
又∵CD=EF,
∴,
∵DF=3,FG=4,BF=BD+DF=BD+3,BG=BD+DF+FG=BD+7,
∴,
∴BD=9,BF=9+3=12,
∴,
解得,AB=6.4m.
答:路灯杆AB的高度为6.4m.
18.(2019秋 建湖县期末)如图,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C落在地板B处、窗户的最低点落在地板是A处,小超测得窗户距地面的高度QD=1m,窗高CD=1.5m,并测得AQ=1m,AB=2m.请根据以上测量数据,求窗外的路灯PH的高度.
【分析】首先根据QD=QE=1m,可得∠QAD=45°,然后证明PH=PA,再证明△PBH∽△QBC,可得,然后代入数值可得方程,解出方程即可得到答案.
【解析】∵DQ⊥BP,
∴∠CQB=90°,
∵QD=1m,QA=1m,
∴∠QAD=45°,
∵PH⊥PB,
∴∠HAP=45°,
∴PH=PA,
设PH=PA=xm,
∵PH⊥PB,CQ⊥PB,
∴PH∥CQ,
∴△PBH∽△QBC,
∴
解得:x=10,经检验:x=10是原方程的解.
答:窗外的路灯PH的高度是10m.
19【答案】 解:过C作CE⊥AB于E,
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴BD=CE=21,CD=BE=2,
设AE=x,
∴ ,
解得:x=14,
∴旗杆的高AB=AE+BE=14+2=16米.
20.【答案】 解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,
∴△BAC∽△FEC、△AC′B∽△E′C′F′,
设AB=x,BC=y
∴
解得 .
∴这棵古树的高为10m.
21.【答案】 (1)∵AB⊥OM,PO⊥OM,
∴ ,
∴ ,
∴ ,
∴OP=8,
即路灯距地面的高度为8米
(2)∵CD⊥OM,PO⊥OM,
∴ ,
∴ ,
∵OC=OA-AC=20-7=13,CD=1.5,OP=8,
∴ ,
∴CN=3,
即小龙的身影的长度为3米
一.选择题
1.有一块直角边AB=4cm,BC=3cm,∠B=90°的Rt△ABC的铁片,现要按照如图所示方式截一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
2. 下列投影中属于中心投影的是( )
A.阳光下跑动的运动员的影子 B.阳光下木杆的影子
C.阳光下汽车的影子 D.路灯下行人的影子
3.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有杆不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
4.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为( )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
5.如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,
长臂外端B升高( )
A.2m B.4m C.4.5m D.8m
6.(2020春 工业园区期末)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为( )
A.3m B.3.2m C.3.4m D.3.6m
7.(2019 临朐县一模)路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
8.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
A. B. C. 11m D.
9.如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.
A. 8 B. 7 C. 6 D. 5
10.如图,在平面直角坐标系xOy中,A(0,2),B(0,2),⊙C的圆心为点C(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E , 则△ABE面积的最大值是
二.填空题
11.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
12.(2020 泰州二模)如图,身高1.6米的小林从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
13.(2020春 大丰区期中)小明想知道学校旗杆的高,他在某一时刻测得直立的标杆高1米时影长0.9米,此时他测旗杆影长时,因为旗杆靠近建筑物,影子不全落在地面上,有一部分影子在墙上,他测得落在地面上的影长BC为2.7米,又测得墙上影高CD为1.2米,旗杆AB的高度为 米.
14.(2019秋 高邮市期末)已知小明身高1.8m,在某一时刻测得他站立在阳光下的影长为0.6m.若当他把手臂竖直举起时,测得影长为0.78m,则小明举起的手臂超出头顶 m.
15.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆高度为15米,则旗杆和标杆之间距离CE长 米.
三.解答题
16(2020 灌云县模拟)如图,在阳光下,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为20m,在墙面上的影长CD为4m,同一时刻,小明又测得竖立于地面长1m的标杆的影长为0.8m,求旗杆AB的高度,
17.(2020 泰州模拟)如图,河对岸有一路灯杆AB,在灯光下,小明在点D处,自己的影长DF=3m,沿BD方向到达点F处再测自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
18(2019秋 建湖县期末)如图,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C落在地板B处、窗户的最低点落在地板是A处,小超测得窗户距地面的高度QD=1m,窗高CD=1.5m,并测得AQ=1m,AB=2m.请根据以上测量数据,求窗外的路灯PH的高度.
19如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
20.李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在C点(如图所示),人在F点正好在镜中看到树尖A;第二次他把镜子放在 处,人在 处正好看到树尖A.已知李师傅眼睛距地面的高度为 ,量得 为 , 为 , 为 ,求树高.
21学习了相似三角形的知识后,爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度,并作出了示意图:如图,路灯(点P)距地面若干米,身高1.6米的小明站在距路灯的底部(O点)20米的A点时,身影的长度AM为5米;
(1)请帮助小明求出路灯距地面的高度;
(2)若另一名身高为1.5米小龙站在直线OA上的C点时,测得他与小明的距离AC为7米,求小龙的身影的长度.
参考答案
一.选择题
1.解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC= AB BC= AC BP,
∴BP=.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴.
设DE=x,则有:,
解得x=,
故选:D.
2.
【答案】
D
【解答】
解:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有选项得到的投影为中心投影.
故选:.
3.答案为:B
4.答案为:C
5.答案为:B.
6.(2020春 工业园区期末)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为( )
A.3m B.3.2m C.3.4m D.3.6m
【分析】直接利用同一时刻物体影子与实际高度成比例,进而得出答案.
【解析】连接AC,过点M作MF⊥PF,
∵同一时刻物体影子与实际高度成比例,
∴,
解得:PF=2.4,
∴PQ=PF+FQ=PF+MN=2.4+0.8=3.2(m),
故选:B.
7.(2019 临朐县一模)路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
【分析】过点G作GQ⊥BE于点Q,GP⊥AB于点P,可得四边形BQGP是矩形,然后且△APG与△FDE相似,然后根据相似三角形对应边成比例列式求出AP的长度,再加上CH即可.
【解析】过点G作GQ⊥BE于点Q,GP⊥AB于点P,
根据题意,四边形BQGP是矩形,
∴BP=GQ=3米,
△APG∽△FDE,
∴,
∴AP,
∴AB3=8.25(米),
故选:C.
8.【答案】 A
解:如图,作DE⊥FC于点E,
∴△ABC∽△CED,∴ .
设AB=x米,由题意得DE=6米,EF=2.2米.∴ ,解得x=5.5.故答案为:A.
9.【答案】 D
解:过点G作GH∥BC , GM⊥BE ,
根据题意,四边形BMGH是矩形,
∴BH=GM=2米,
△AHG∽△FDE ,
∴ = ,
∴AH=3,
∴AB=2+3=5米.
故选D .
10.【答案】 D
【解析】
【解答】若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
Rt△ACD中,CD=1,AC=OC+OA=3;
由勾股定理,得:AD=2;
∴S△ACD=AD CD=;
易证得△AOE∽△ADC,
∴=()2=()2=,
即S△AOE=S△ADC=;
∴S△ABE=S△AOB-S△AOE=×2×2-=2-;
故选D.
二.填空题
11.解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴AB=4.5(米),
故答案为:4.5.
12.(2020 泰州二模)如图,身高1.6米的小林从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 8 米.
【分析】根据CD∥AB,得出△ECD∽△EBA,进而得出比例式求出即可.
【解析】由题意知,CE=2米,CD=1.6米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴,即,
解得AB=8(米),
即路灯的高AB为8米;
故答案为:8米.
13.(2020春 大丰区期中)小明想知道学校旗杆的高,他在某一时刻测得直立的标杆高1米时影长0.9米,此时他测旗杆影长时,因为旗杆靠近建筑物,影子不全落在地面上,有一部分影子在墙上,他测得落在地面上的影长BC为2.7米,又测得墙上影高CD为1.2米,旗杆AB的高度为 4.2 米.
【分析】过点D作DE⊥AB于点E,则BE=CD=1.2m,再根据同一时刻物高与影长成正比求出AE的长,进而可得出结论.
【解析】过点D作DE⊥AB于点E,则BE=CD=1.2m,
∵他在某一时刻测得直立的标杆高1米时影长0.9米,
∴,即,
解得:AE=3m,
∴AB=AE+BE=3+1.2=4.2(m).
故答案为:4.2.
14.(2019秋 高邮市期末)已知小明身高1.8m,在某一时刻测得他站立在阳光下的影长为0.6m.若当他把手臂竖直举起时,测得影长为0.78m,则小明举起的手臂超出头顶 0.54 m.
【分析】根据在同一时物体的高度和影长成正比,设出手臂竖直举起时总高度x,即可列方程解出x的值,再减去身高即可得出小明举起的手臂超出头顶的高度.
【解析】设手臂竖直举起时总高度xm,列方程得:,
解得x=2.34,
2.34﹣1.8=0.54m,
所以小明举起的手臂超出头顶的高度为0.54m.
故答案为:0.54.
15.解:如图,延长FB交EA的延长线于T,设TA=x米,EC=y米.
由题意,AB=1.5米,AC=CD=3米,EF=15米.
∵AB∥CD,
∴△TAB∽△TCD,
∴=,
∴=,
解得x=3,
经检验x=3是分式方程的解,
∵CD∥EF,
∴△TCD∽△TEF,
∴=,
∴=,
∴y=24,
经检验y=24是分式方程的解,
∴EC=24(米),
故答案为:24.
三.解答题
16.(2020 灌云县模拟)如图,在阳光下,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为20m,在墙面上的影长CD为4m,同一时刻,小明又测得竖立于地面长1m的标杆的影长为0.8m,求旗杆AB的高度,
【分析】作DE⊥AB于E,可得矩形BCDE,利用同一时刻物高与影长的比一定得到AE的长度,加上CD的长度即为旗杆的高度.
【解析】作DE⊥AB于E,
∵DC⊥BC于C,AB⊥BC于B,
∴四边形BCDE为矩形,
∴DE=BC=20m,BE=DC=4m,
∵同一时刻物高与影长所组成的三角形相似,
∴,
解得AE=25m,
∴AB=25+4=29m.
答:旗杆的高度为29m.
17.(2020 泰州模拟)如图,河对岸有一路灯杆AB,在灯光下,小明在点D处,自己的影长DF=3m,沿BD方向到达点F处再测自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
【分析】在同一时刻物高和影长成正比,根据相似三角形的性质即可解答.
【解析】∵CD∥EF∥AB,
∴可以得到△CDF∽△ABF,△ABG∽△EFG,
∴,,
又∵CD=EF,
∴,
∵DF=3,FG=4,BF=BD+DF=BD+3,BG=BD+DF+FG=BD+7,
∴,
∴BD=9,BF=9+3=12,
∴,
解得,AB=6.4m.
答:路灯杆AB的高度为6.4m.
18.(2019秋 建湖县期末)如图,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C落在地板B处、窗户的最低点落在地板是A处,小超测得窗户距地面的高度QD=1m,窗高CD=1.5m,并测得AQ=1m,AB=2m.请根据以上测量数据,求窗外的路灯PH的高度.
【分析】首先根据QD=QE=1m,可得∠QAD=45°,然后证明PH=PA,再证明△PBH∽△QBC,可得,然后代入数值可得方程,解出方程即可得到答案.
【解析】∵DQ⊥BP,
∴∠CQB=90°,
∵QD=1m,QA=1m,
∴∠QAD=45°,
∵PH⊥PB,
∴∠HAP=45°,
∴PH=PA,
设PH=PA=xm,
∵PH⊥PB,CQ⊥PB,
∴PH∥CQ,
∴△PBH∽△QBC,
∴
解得:x=10,经检验:x=10是原方程的解.
答:窗外的路灯PH的高度是10m.
19【答案】 解:过C作CE⊥AB于E,
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴BD=CE=21,CD=BE=2,
设AE=x,
∴ ,
解得:x=14,
∴旗杆的高AB=AE+BE=14+2=16米.
20.【答案】 解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,
∴△BAC∽△FEC、△AC′B∽△E′C′F′,
设AB=x,BC=y
∴
解得 .
∴这棵古树的高为10m.
21.【答案】 (1)∵AB⊥OM,PO⊥OM,
∴ ,
∴ ,
∴ ,
∴OP=8,
即路灯距地面的高度为8米
(2)∵CD⊥OM,PO⊥OM,
∴ ,
∴ ,
∵OC=OA-AC=20-7=13,CD=1.5,OP=8,
∴ ,
∴CN=3,
即小龙的身影的长度为3米
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
