1.1.3等腰三角形 课件(共30张PPT)
文档属性
| 名称 | 1.1.3等腰三角形 课件(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 20:22:17 | ||
图片预览






文档简介
(共30张PPT)
新知导入
画一画:根据图中的提示补全下列各等腰三角形,试着发现它们的规律.
1 等腰三角形
第3课时
1. 探索并证明等腰三角形的判定定理,并能运用其解决简单的几何证明问题;
2. 知道反证法的基本证明思路,能简单应用;
3. 在学习过程中不断发展逻辑推理能力.
学习目标
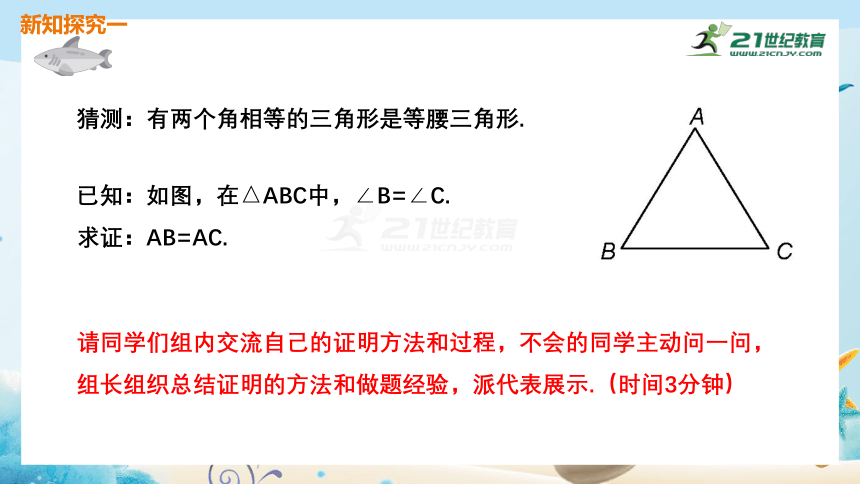
猜测:有两个角相等的三角形是等腰三角形.
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
请同学们独立思考,写出证明过程,时间3分钟.
新知探究一
猜测:有两个角相等的三角形是等腰三角形.
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
请同学们组内交流自己的证明方法和过程,不会的同学主动问一问,组长组织总结证明的方法和做题经验,派代表展示.(时间3分钟)
新知探究一
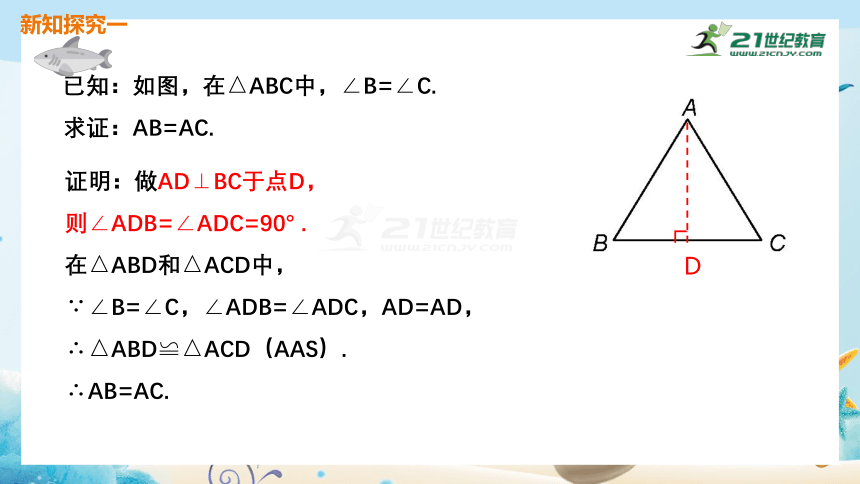
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
D
证明:做AD⊥BC于点D,
则∠ADB=∠ADC=90° .
在△ABD和△ACD中,
∵∠B=∠C,∠ADB=∠ADC,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
新知探究一
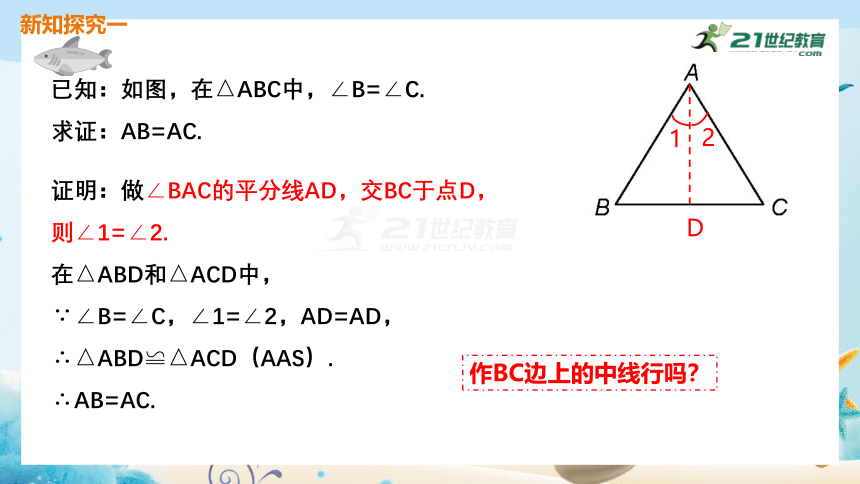
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
D
证明:做∠BAC的平分线AD,交BC于点D,
则∠1=∠2.
在△ABD和△ACD中,
∵∠B=∠C,∠1=∠2,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
2
1
作BC边上的中线行吗?
新知探究一
等腰三角形的判定定理:
有两个角相等的三角形是等腰三角形.
(简述为:等角对等边)
如图:在△ABC中,
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
即△ABC是等腰三角形.
新知探究一
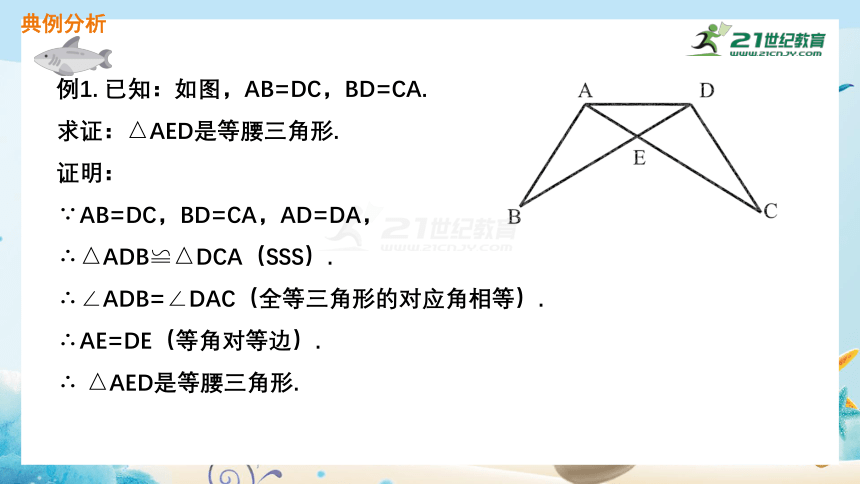
例1. 已知:如图,AB=DC,BD=CA.
求证:△AED是等腰三角形.
证明:
∵AB=DC,BD=CA,AD=DA,
∴△ADB≌△DCA(SSS).
∴∠ADB=∠DAC(全等三角形的对应角相等).
∴AE=DE(等角对等边).
∴ △AED是等腰三角形.
典例分析
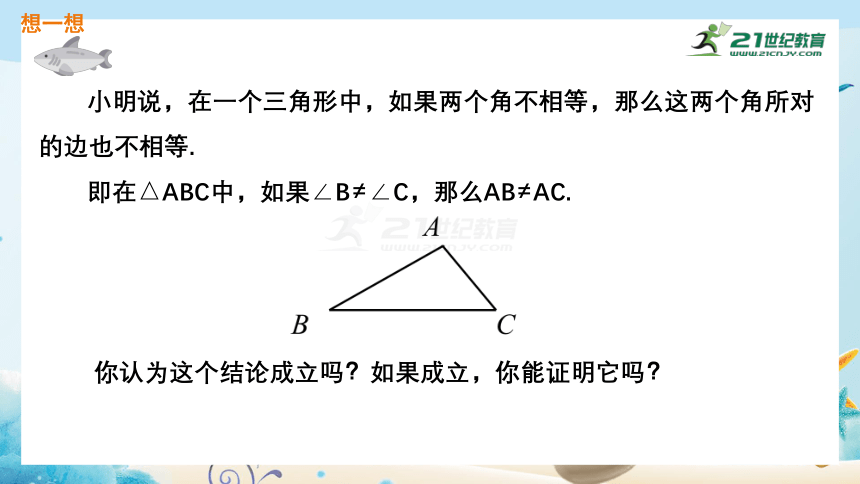
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
即在△ABC中,如果∠B≠∠C,那么AB≠AC.
你认为这个结论成立吗?如果成立,你能证明它吗?
想一想
古时候,王戎7岁时和小伙伴外出游玩,看到了路边的李子树上结满了李子小伙伴们争相跑去摘李子,只有王戎原地不动有人问他为什么他说:“树在道边而多子,此必苦李。小伙伴摘来果实一尝,果然是苦李。
王戎是怎样知道李子是苦的呢?
他运用了怎样的推理方法?
证明命题的新思路
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
即在△ABC中,如果∠B≠∠C,那么AB≠AC.
上面这个问题你能试着解释吗?
想一想
小明是这样想的:
如图,在△ABC中,已知∠B≠∠C,此时,AB与AC要么相等,要么不相等.
假设AB=AC,那么根据“等边对等角”定理得∠B=∠C,但已知条件是∠B≠∠C.
“∠B=∠C”与已知条件“∠B≠∠C”相矛盾,
因此AB ≠ AC.
想一想
小明在证明时,先假设命题的结论不成立,然后推导出与定义、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立. 这种证明方法称为反证法(reduction to absurdity).
想一想
例3:用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设∠A和∠B是直角,即∠A=90°,∠B=90°.
于是∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B是直角”的假设不成立.
所以,一个三角形中不能有两个角是直角.
典例分析
反证法的一般步骤:
1. 假设:先假设命题的结论不成立:即结论的反面成立;
2. 归谬:从这个假设出发,应用正确的推论方法,得出与定义、公理、已有定理或已知条件相矛盾的结果;
3. 结论:由矛盾的结果判定假设不正确,从而肯定命题的结论正确.
归纳总结
课程讲授
练一练:在△ABC中,∠A与∠B的度数如下,则能判定△ABC为等腰三角形的是( )
A.∠A=60°,∠B=50°
B.∠A=70°,∠B=60°
C.∠A=40°,∠B=70°
D.∠A=40°,∠B=80°
1
等角对等边
C
课程讲授
2
反证法
想一想:小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗 如果成立,你能证明它吗
在△ABC中, 如果∠B≠∠C,那么AB≠AC.
A
B
C
课程讲授
2
反证法
C
A
B
如图,在△ABC中,已知∠B≠∠C,
此时, AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等角对等边”定理可得∠B=∠C, 但已知条件是 ∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾,因此AB≠AC.
小明是这样想的:
你能理解他的推理过程吗
课程讲授
2
反证法
在证明时,先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
用反证法证题的一般步骤:
1. 假设: 先假设命题的结论不成立;
2. 归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
3. 结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
课程讲授
2
反证法
课程讲授
2
反证法
例2 用反证法证明:一个三角形中不能有两个角是直角.已知:△ABC.
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设∠A=∠B=90°,则
∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,∠A=∠B=90°不成立.
所以一个三角形中不能有两个角是直角.
随堂练习
1.如图,已知OC平分∠AOB,CD∥OB,若OD=8 cm,则CD等于( )
A.8 cm
B.4 cm
C.15 cm
D.20 cm
A
随堂练习
2.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个
B.4个
C.3个
D.2个
A
随堂练习
3.在如图所示的三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③
B.①②④
C.②③④
D.①③④
D
假设____________,那么_________.
这与“______________________________________ ________________”矛盾.
所以___________,即求证的命题正确.
证明:
因为已知_________,
所以过直线l2外一点P,有两条直线和l2平行,
随堂练习
4.求证:在同一平面内,如果一条直线和两条平行直线中的一条相交,那么和另一条也相交.
已知:
直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.
求证:
l3与l2相交.
l1
l2
l3
P
经过直线外一点,有且只有一条直线
与已知直线平行
假设不成立
l3与l2 不相交
l3∥l2
l1∥l2
随堂练习
5.如图,在△ABC中,AB=AC,D是AB上一点,过D作DE⊥BC于点E,并与CA的延长线相交于点F,试判断△ADF的形状,并说明理由.
解:△ADF是等腰三角形.
理由:在△ABC中.
∵AB=AC,∴∠B=∠C.
∵DE⊥BC,∴∠DEB=∠DEC=90°,
∴∠BDE+∠B=90°,∠F+∠C=90°,∴∠BDE=∠F.
∵∠BDE=∠ADF,∴∠ADF=∠F,∴AF=AD,
∴△ADF是等腰三角形.
课堂小结
等腰三角形的判定
等角对等边
反证法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
先假设结论不成立,然后推导与已知定理相矛盾的结果,从而证明原命题成立.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
新知导入
画一画:根据图中的提示补全下列各等腰三角形,试着发现它们的规律.
1 等腰三角形
第3课时
1. 探索并证明等腰三角形的判定定理,并能运用其解决简单的几何证明问题;
2. 知道反证法的基本证明思路,能简单应用;
3. 在学习过程中不断发展逻辑推理能力.
学习目标
猜测:有两个角相等的三角形是等腰三角形.
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
请同学们独立思考,写出证明过程,时间3分钟.
新知探究一
猜测:有两个角相等的三角形是等腰三角形.
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
请同学们组内交流自己的证明方法和过程,不会的同学主动问一问,组长组织总结证明的方法和做题经验,派代表展示.(时间3分钟)
新知探究一
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
D
证明:做AD⊥BC于点D,
则∠ADB=∠ADC=90° .
在△ABD和△ACD中,
∵∠B=∠C,∠ADB=∠ADC,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
新知探究一
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
D
证明:做∠BAC的平分线AD,交BC于点D,
则∠1=∠2.
在△ABD和△ACD中,
∵∠B=∠C,∠1=∠2,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
2
1
作BC边上的中线行吗?
新知探究一
等腰三角形的判定定理:
有两个角相等的三角形是等腰三角形.
(简述为:等角对等边)
如图:在△ABC中,
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
即△ABC是等腰三角形.
新知探究一
例1. 已知:如图,AB=DC,BD=CA.
求证:△AED是等腰三角形.
证明:
∵AB=DC,BD=CA,AD=DA,
∴△ADB≌△DCA(SSS).
∴∠ADB=∠DAC(全等三角形的对应角相等).
∴AE=DE(等角对等边).
∴ △AED是等腰三角形.
典例分析
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
即在△ABC中,如果∠B≠∠C,那么AB≠AC.
你认为这个结论成立吗?如果成立,你能证明它吗?
想一想
古时候,王戎7岁时和小伙伴外出游玩,看到了路边的李子树上结满了李子小伙伴们争相跑去摘李子,只有王戎原地不动有人问他为什么他说:“树在道边而多子,此必苦李。小伙伴摘来果实一尝,果然是苦李。
王戎是怎样知道李子是苦的呢?
他运用了怎样的推理方法?
证明命题的新思路
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.
即在△ABC中,如果∠B≠∠C,那么AB≠AC.
上面这个问题你能试着解释吗?
想一想
小明是这样想的:
如图,在△ABC中,已知∠B≠∠C,此时,AB与AC要么相等,要么不相等.
假设AB=AC,那么根据“等边对等角”定理得∠B=∠C,但已知条件是∠B≠∠C.
“∠B=∠C”与已知条件“∠B≠∠C”相矛盾,
因此AB ≠ AC.
想一想
小明在证明时,先假设命题的结论不成立,然后推导出与定义、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立. 这种证明方法称为反证法(reduction to absurdity).
想一想
例3:用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设∠A和∠B是直角,即∠A=90°,∠B=90°.
于是∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B是直角”的假设不成立.
所以,一个三角形中不能有两个角是直角.
典例分析
反证法的一般步骤:
1. 假设:先假设命题的结论不成立:即结论的反面成立;
2. 归谬:从这个假设出发,应用正确的推论方法,得出与定义、公理、已有定理或已知条件相矛盾的结果;
3. 结论:由矛盾的结果判定假设不正确,从而肯定命题的结论正确.
归纳总结
课程讲授
练一练:在△ABC中,∠A与∠B的度数如下,则能判定△ABC为等腰三角形的是( )
A.∠A=60°,∠B=50°
B.∠A=70°,∠B=60°
C.∠A=40°,∠B=70°
D.∠A=40°,∠B=80°
1
等角对等边
C
课程讲授
2
反证法
想一想:小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗 如果成立,你能证明它吗
在△ABC中, 如果∠B≠∠C,那么AB≠AC.
A
B
C
课程讲授
2
反证法
C
A
B
如图,在△ABC中,已知∠B≠∠C,
此时, AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等角对等边”定理可得∠B=∠C, 但已知条件是 ∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾,因此AB≠AC.
小明是这样想的:
你能理解他的推理过程吗
课程讲授
2
反证法
在证明时,先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
用反证法证题的一般步骤:
1. 假设: 先假设命题的结论不成立;
2. 归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
3. 结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
课程讲授
2
反证法
课程讲授
2
反证法
例2 用反证法证明:一个三角形中不能有两个角是直角.已知:△ABC.
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设∠A=∠B=90°,则
∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,∠A=∠B=90°不成立.
所以一个三角形中不能有两个角是直角.
随堂练习
1.如图,已知OC平分∠AOB,CD∥OB,若OD=8 cm,则CD等于( )
A.8 cm
B.4 cm
C.15 cm
D.20 cm
A
随堂练习
2.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个
B.4个
C.3个
D.2个
A
随堂练习
3.在如图所示的三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.①②③
B.①②④
C.②③④
D.①③④
D
假设____________,那么_________.
这与“______________________________________ ________________”矛盾.
所以___________,即求证的命题正确.
证明:
因为已知_________,
所以过直线l2外一点P,有两条直线和l2平行,
随堂练习
4.求证:在同一平面内,如果一条直线和两条平行直线中的一条相交,那么和另一条也相交.
已知:
直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.
求证:
l3与l2相交.
l1
l2
l3
P
经过直线外一点,有且只有一条直线
与已知直线平行
假设不成立
l3与l2 不相交
l3∥l2
l1∥l2
随堂练习
5.如图,在△ABC中,AB=AC,D是AB上一点,过D作DE⊥BC于点E,并与CA的延长线相交于点F,试判断△ADF的形状,并说明理由.
解:△ADF是等腰三角形.
理由:在△ABC中.
∵AB=AC,∴∠B=∠C.
∵DE⊥BC,∴∠DEB=∠DEC=90°,
∴∠BDE+∠B=90°,∠F+∠C=90°,∴∠BDE=∠F.
∵∠BDE=∠ADF,∴∠ADF=∠F,∴AF=AD,
∴△ADF是等腰三角形.
课堂小结
等腰三角形的判定
等角对等边
反证法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
先假设结论不成立,然后推导与已知定理相矛盾的结果,从而证明原命题成立.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
