2021--2022学年北师大版七年级数学下册2.1两条直线的位置关系课后训练A(Word版含答案)
文档属性
| 名称 | 2021--2022学年北师大版七年级数学下册2.1两条直线的位置关系课后训练A(Word版含答案) | 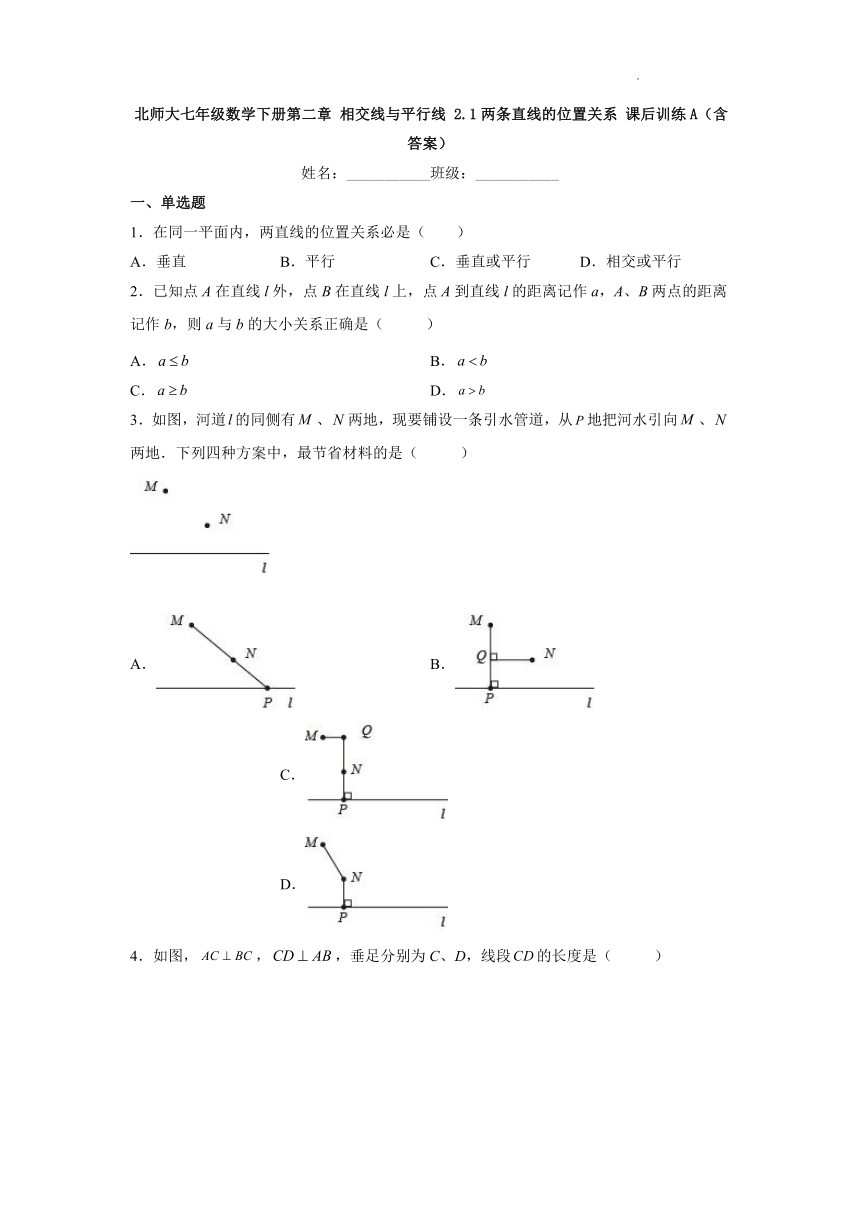 | |
| 格式 | docx | ||
| 文件大小 | 313.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 11:53:00 | ||
图片预览

文档简介
北师大七年级数学下册第二章 相交线与平行线 2.1两条直线的位置关系 课后训练A(含答案)
姓名:___________班级:___________
一、单选题
1.在同一平面内,两直线的位置关系必是( )
A.垂直 B.平行 C.垂直或平行 D.相交或平行
2.已知点A在直线l外,点B在直线l上,点A到直线l的距离记作a,A、B两点的距离记作b,则a与b的大小关系正确是( )
A. B.
C. D.
3.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B. C. D.
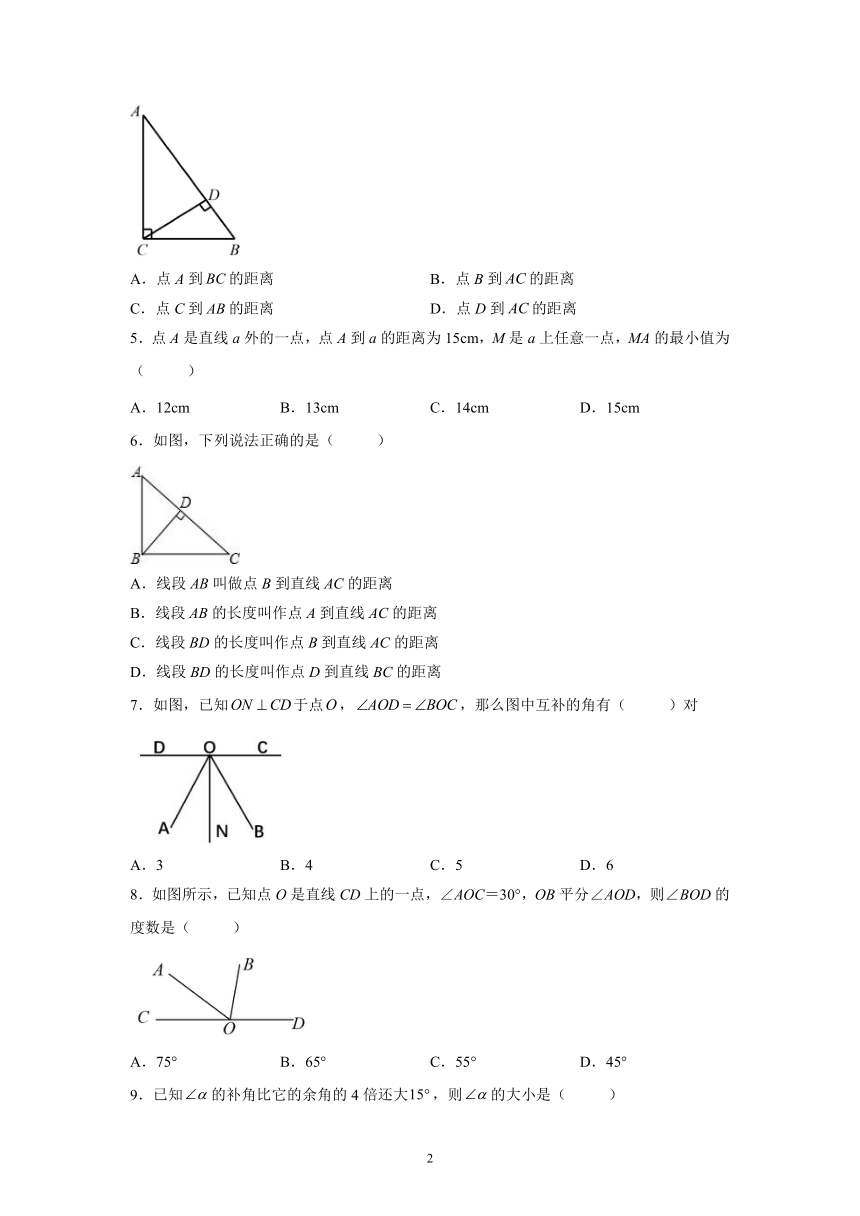
4.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
5.点A是直线a外的一点,点A到a的距离为15cm,M是a上任意一点,MA的最小值为( )
A.12cm B.13cm C.14cm D.15cm
6.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点B到直线AC的距离
D.线段BD的长度叫作点D到直线BC的距离
7.如图,已知于点,,那么图中互补的角有( )对
A.3 B.4 C.5 D.6
8.如图所示,已知点O是直线CD上的一点,∠AOC=30°,OB平分∠AOD,则∠BOD的度数是( )
A.75° B.65° C.55° D.45°
9.已知的补角比它的余角的4倍还大,则的大小是( )
A. B. C. D.
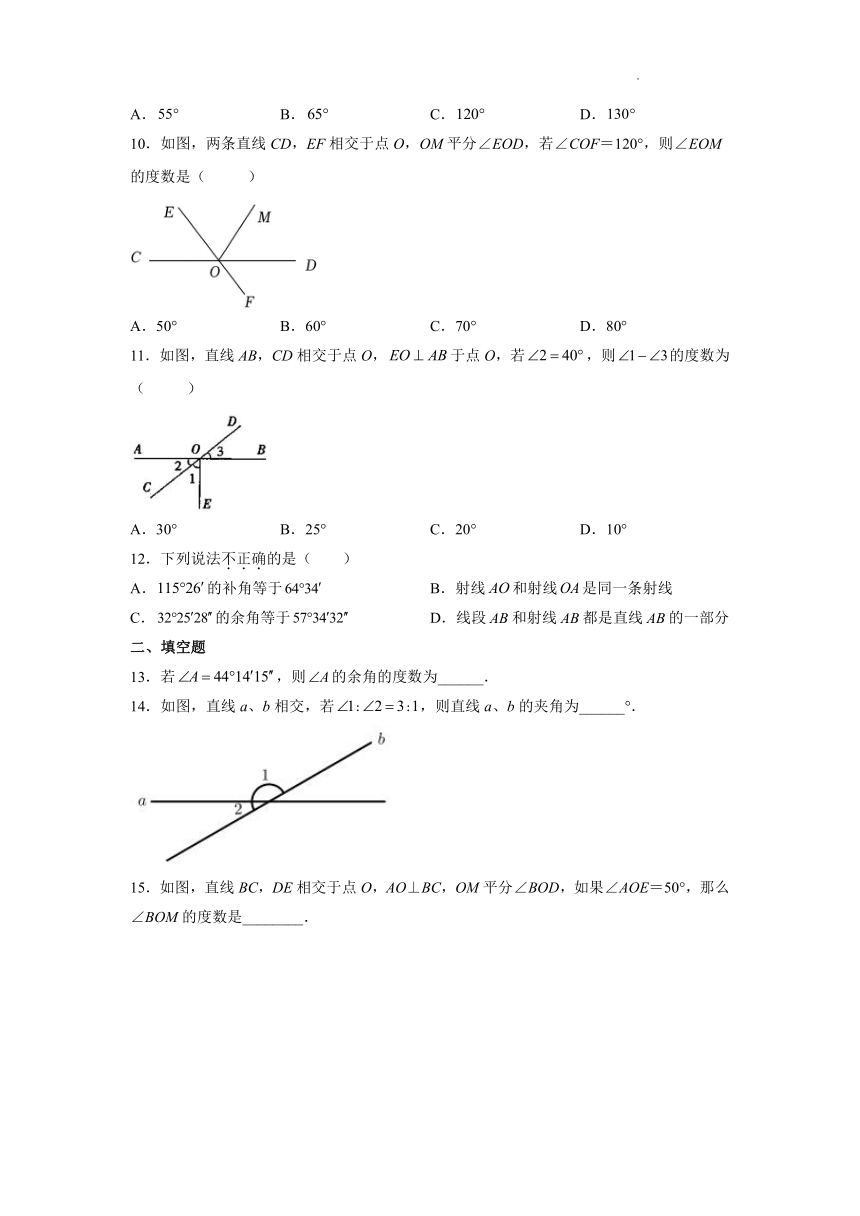
10.如图,两条直线CD,EF相交于点O,OM平分∠EOD,若∠COF=120°,则∠EOM的度数是( )
A.50° B.60° C.70° D.80°
11.如图,直线AB,CD相交于点O,于点O,若,则的度数为( )
A.30° B.25° C.20° D.10°
12.下列说法不正确的是( )
A.的补角等于 B.射线和射线是同一条射线
C.的余角等于 D.线段和射线都是直线的一部分
二、填空题
13.若,则的余角的度数为______.
14.如图,直线a、b相交,若,则直线a、b的夹角为______°.
15.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是________.
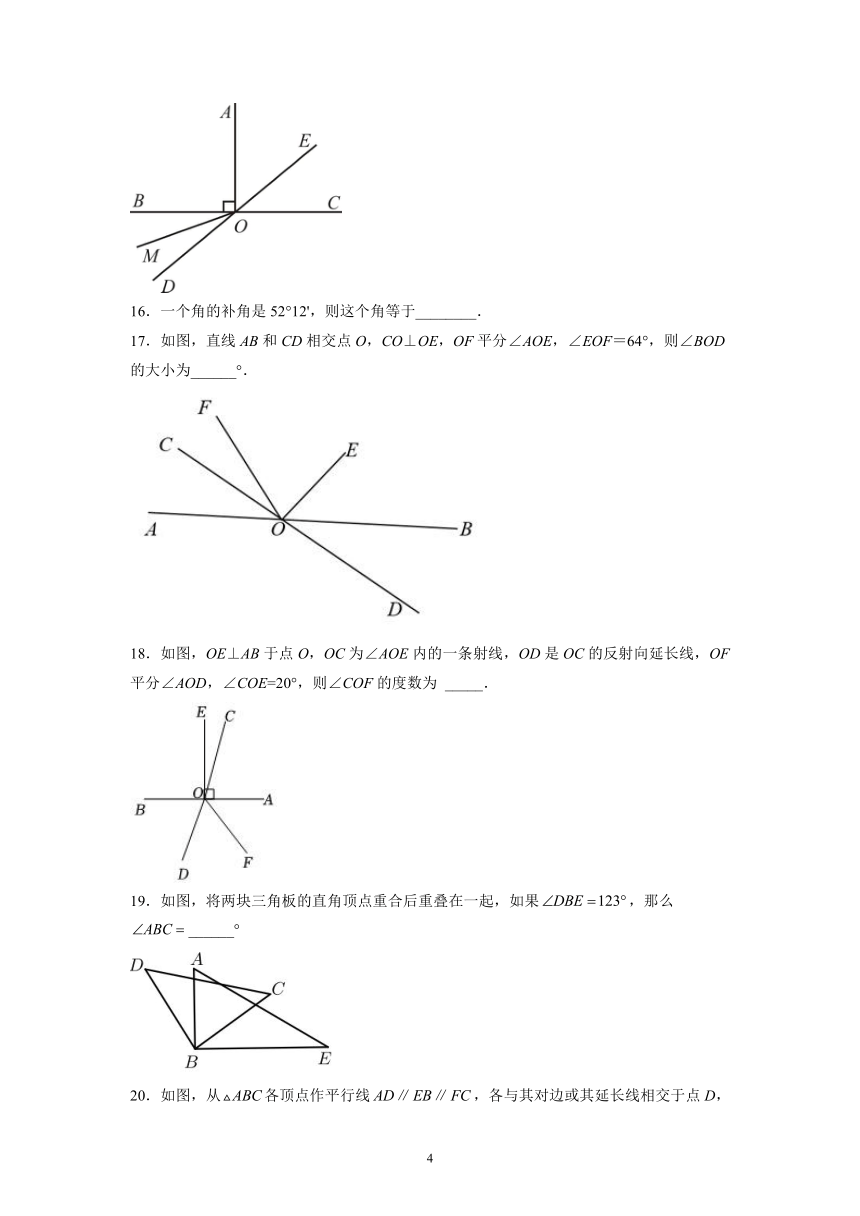
16.一个角的补角是52°12',则这个角等于________.
17.如图,直线AB和CD相交点O,CO⊥OE,OF平分∠AOE,∠EOF=64°,则∠BOD的大小为______°.
18.如图,OE⊥AB于点O,OC为∠AOE内的一条射线,OD是OC的反射向延长线,OF平分∠AOD,∠COE=20°,则∠COF的度数为 _____.
19.如图,将两块三角板的直角顶点重合后重叠在一起,如果,那么______°
20.如图,从各顶点作平行线,各与其对边或其延长线相交于点D,E,F.若的面积为5,则的面积为______.
三、解答题
21.如图,平面上有3个点,,.
(1)画线段,射线和直线;
(2)过点画直线的垂线,垂足为,比较______(填“>”或“=”或“<”),能说明这个结论正确的依据是:连结直线外一点与直线上各点的所有线段中,______.
22.如图,在高速公路的同一侧有、两座城市.
(1)现在要以最低成本在、两座城市之间修建一条公路,假设每公里修建的成本相同,试在图中画出这条公路的位置,并简要说明你的依据;
(2)若要在高速公路边建一个停靠站,使得城市的人到该停靠点最方便(即距离最近),请在图中标出的位置,并简要说明你的依据.
23.如图,已知∠AOC=90°,∠BOD=90°,∠BOC=38°19′,求∠AOD的度数.
24.如图,点O在直线AB上,已知∠1=30°,∠2∠COE,
(1)求∠2的度数;
(2)若OD平分∠BOC,求∠3和∠COE的度数.
25.如图,与互为补角,与互为余角,且.
(1)求的度数;
(2)若平分,求的度数.
26.如图,直线AB、CD相交于O点,∠AOC=70°,∠BOE=35°,
(1)∠DOE的度数;
(2)若OF平分∠AOD,射线OE与OF之间有什么位置关系?为什么?
27.如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2:∠1=4:1,求∠AOF.
28.如图,直线,相交于点,,是的平分线,是的反向延长线.
(1)求、的度数;
(2)说明平分的理由.
29.如图,直线AB、CD相交于点O,OE平分∠BOD,OE⊥OF.
(1)若∠DOE=32°,求∠BOF的度数;
(2)若∠COE:∠COF=8:3,求∠AOF的度数.
30.【实践操作】三角尺中的数学
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,∠ACD=∠ECB=90°.
①若∠ECD=35°,则∠ACB=______;若∠ACB=140°,则∠ECD=______;
②猜想∠ACB与∠ECD的大小有何特殊关系,并说明理由;
(2)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,∠ACD=∠AFG=90°,则∠GAC与∠DAF的大小又有何关系,请说明理由.
参考答案:
1.D 2.A 3.D 4.C 5.D 6.C 7.C 8.A 9.B 10.B 11.D 12.B
13.
14.
15.20°/20度
16.
17.38
18.125°/125度
19.57
20.10
21.(1)略 (2)>,垂线段最短
22.(1)两点之间,线段最短
23.141°41′
24.(1)∠2=50°;
(2)∠3=25°,∠COE=100°.
25.(1)72°
(2)126°
26.(1)35°;
(2)OE⊥OF
27.
28.(1),;
(2)略.
29.(1)58°
(2)126°
30.(1)①145°,40°;②∠ACB+∠ECD=180°(或∠ACB与∠ECD互补)
(2)∠GAC+∠DAF=120°
姓名:___________班级:___________
一、单选题
1.在同一平面内,两直线的位置关系必是( )
A.垂直 B.平行 C.垂直或平行 D.相交或平行
2.已知点A在直线l外,点B在直线l上,点A到直线l的距离记作a,A、B两点的距离记作b,则a与b的大小关系正确是( )
A. B.
C. D.
3.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B. C. D.
4.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
5.点A是直线a外的一点,点A到a的距离为15cm,M是a上任意一点,MA的最小值为( )
A.12cm B.13cm C.14cm D.15cm
6.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点B到直线AC的距离
D.线段BD的长度叫作点D到直线BC的距离
7.如图,已知于点,,那么图中互补的角有( )对
A.3 B.4 C.5 D.6
8.如图所示,已知点O是直线CD上的一点,∠AOC=30°,OB平分∠AOD,则∠BOD的度数是( )
A.75° B.65° C.55° D.45°
9.已知的补角比它的余角的4倍还大,则的大小是( )
A. B. C. D.
10.如图,两条直线CD,EF相交于点O,OM平分∠EOD,若∠COF=120°,则∠EOM的度数是( )
A.50° B.60° C.70° D.80°
11.如图,直线AB,CD相交于点O,于点O,若,则的度数为( )
A.30° B.25° C.20° D.10°
12.下列说法不正确的是( )
A.的补角等于 B.射线和射线是同一条射线
C.的余角等于 D.线段和射线都是直线的一部分
二、填空题
13.若,则的余角的度数为______.
14.如图,直线a、b相交,若,则直线a、b的夹角为______°.
15.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是________.
16.一个角的补角是52°12',则这个角等于________.
17.如图,直线AB和CD相交点O,CO⊥OE,OF平分∠AOE,∠EOF=64°,则∠BOD的大小为______°.
18.如图,OE⊥AB于点O,OC为∠AOE内的一条射线,OD是OC的反射向延长线,OF平分∠AOD,∠COE=20°,则∠COF的度数为 _____.
19.如图,将两块三角板的直角顶点重合后重叠在一起,如果,那么______°
20.如图,从各顶点作平行线,各与其对边或其延长线相交于点D,E,F.若的面积为5,则的面积为______.
三、解答题
21.如图,平面上有3个点,,.
(1)画线段,射线和直线;
(2)过点画直线的垂线,垂足为,比较______(填“>”或“=”或“<”),能说明这个结论正确的依据是:连结直线外一点与直线上各点的所有线段中,______.
22.如图,在高速公路的同一侧有、两座城市.
(1)现在要以最低成本在、两座城市之间修建一条公路,假设每公里修建的成本相同,试在图中画出这条公路的位置,并简要说明你的依据;
(2)若要在高速公路边建一个停靠站,使得城市的人到该停靠点最方便(即距离最近),请在图中标出的位置,并简要说明你的依据.
23.如图,已知∠AOC=90°,∠BOD=90°,∠BOC=38°19′,求∠AOD的度数.
24.如图,点O在直线AB上,已知∠1=30°,∠2∠COE,
(1)求∠2的度数;
(2)若OD平分∠BOC,求∠3和∠COE的度数.
25.如图,与互为补角,与互为余角,且.
(1)求的度数;
(2)若平分,求的度数.
26.如图,直线AB、CD相交于O点,∠AOC=70°,∠BOE=35°,
(1)∠DOE的度数;
(2)若OF平分∠AOD,射线OE与OF之间有什么位置关系?为什么?
27.如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2:∠1=4:1,求∠AOF.
28.如图,直线,相交于点,,是的平分线,是的反向延长线.
(1)求、的度数;
(2)说明平分的理由.
29.如图,直线AB、CD相交于点O,OE平分∠BOD,OE⊥OF.
(1)若∠DOE=32°,求∠BOF的度数;
(2)若∠COE:∠COF=8:3,求∠AOF的度数.
30.【实践操作】三角尺中的数学
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,∠ACD=∠ECB=90°.
①若∠ECD=35°,则∠ACB=______;若∠ACB=140°,则∠ECD=______;
②猜想∠ACB与∠ECD的大小有何特殊关系,并说明理由;
(2)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,∠ACD=∠AFG=90°,则∠GAC与∠DAF的大小又有何关系,请说明理由.
参考答案:
1.D 2.A 3.D 4.C 5.D 6.C 7.C 8.A 9.B 10.B 11.D 12.B
13.
14.
15.20°/20度
16.
17.38
18.125°/125度
19.57
20.10
21.(1)略 (2)>,垂线段最短
22.(1)两点之间,线段最短
23.141°41′
24.(1)∠2=50°;
(2)∠3=25°,∠COE=100°.
25.(1)72°
(2)126°
26.(1)35°;
(2)OE⊥OF
27.
28.(1),;
(2)略.
29.(1)58°
(2)126°
30.(1)①145°,40°;②∠ACB+∠ECD=180°(或∠ACB与∠ECD互补)
(2)∠GAC+∠DAF=120°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
