第五章 相交线与平行线 单元复习课件(共28张PPT)
文档属性
| 名称 | 第五章 相交线与平行线 单元复习课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:38:28 | ||
图片预览





文档简介
第五章 相交线与平行线
人教版 七年级下册
直线的位置关系:在同一平面内,不重合的两条直线之间的位置关系只有两种:相交或平行。
知识点一 相交线
【典例1】a、b、c是平面上任意三条直线,交点可以有( ) A.1个或2个或3个 B. 0个或1个或2个或3个 C.1个或2个 D. 都不对
B
概念:当两条相交直线所成的四个角中,有一个角是直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,交点叫做垂足。
表示方法:
如图,a ⊥ b,垂足为O.
记作:a ⊥ b于点O.
垂线
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线的画法:一落、二移、三画。
垂线段最短定理:连接直线外一点与直线上各点的所有线段中,垂线段最短。
【注意事项】
1.线段与线段,线段与射线,线段与直线,射线与射线,射线与直线垂直,是特指它们所在的直线互相垂直。
2.两条直线互相垂直,则它们之间所形成的四个角为直角;若两条直线的夹角为直角,则这两条直线互相垂直。
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
注意:
1.垂线是一条直线,而垂线段是一条线段。
2.经过直线外一点到这条直线的垂线段有且只有一条。
3.经过一点画射线或线段的垂线,是指它们所在直线的垂线,垂足的位置不固定,可能会出现在射线的反向延长线或线段的延长线上。
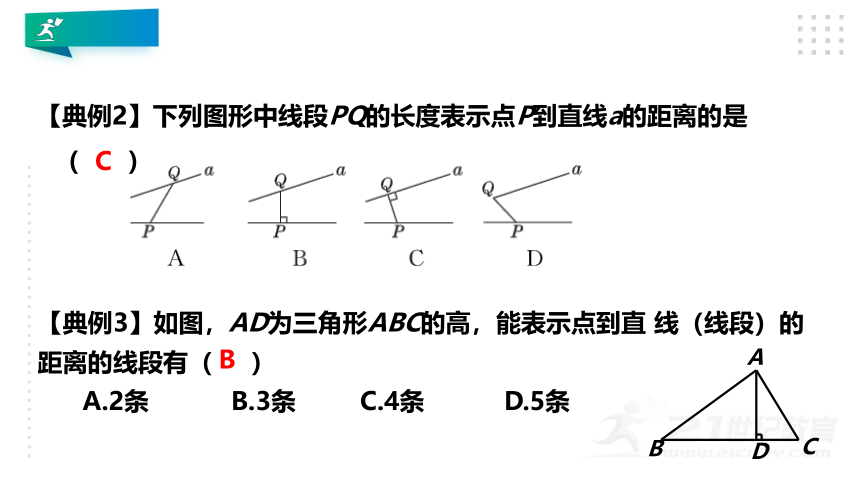
【典例3】如图,AD为三角形ABC的高,能表示点到直 线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
B
C
D
A
B
【典例2】下列图形中线段PQ的长度表示点P到直线a的距离的是( )
C
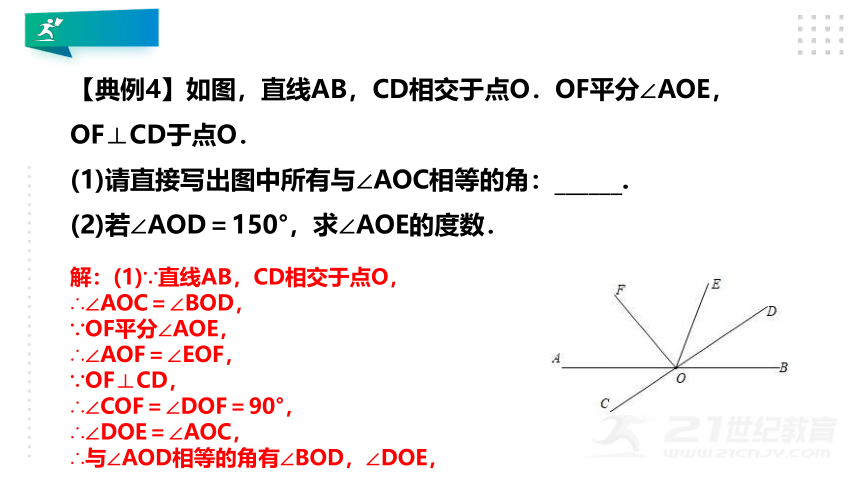
【典例4】如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O. (1)请直接写出图中所有与∠AOC相等的角:______. (2)若∠AOD=150°,求∠AOE的度数.
解:(1)∵直线AB,CD相交于点O, ∴∠AOC=∠BOD, ∵OF平分∠AOE, ∴∠AOF=∠EOF, ∵OF⊥CD, ∴∠COF=∠DOF=90°, ∴∠DOE=∠AOC, ∴与∠AOD相等的角有∠BOD,∠DOE,
解:(2)∵OF⊥CD, ∴∠DOF=90°, ∵∠AOD=150°, ∴∠AOF=60°, ∵OF平分∠AOE, ∴∠AOE=2∠AOF=120°.
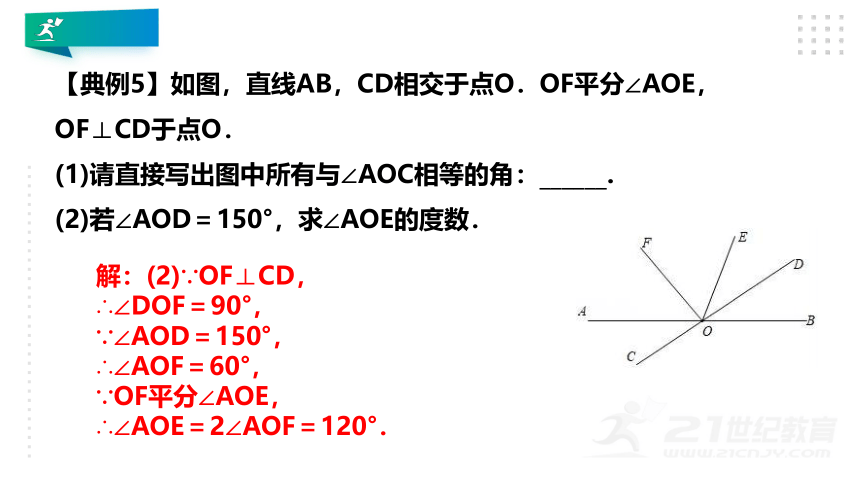
【典例5】如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O. (1)请直接写出图中所有与∠AOC相等的角:______. (2)若∠AOD=150°,求∠AOE的度数.
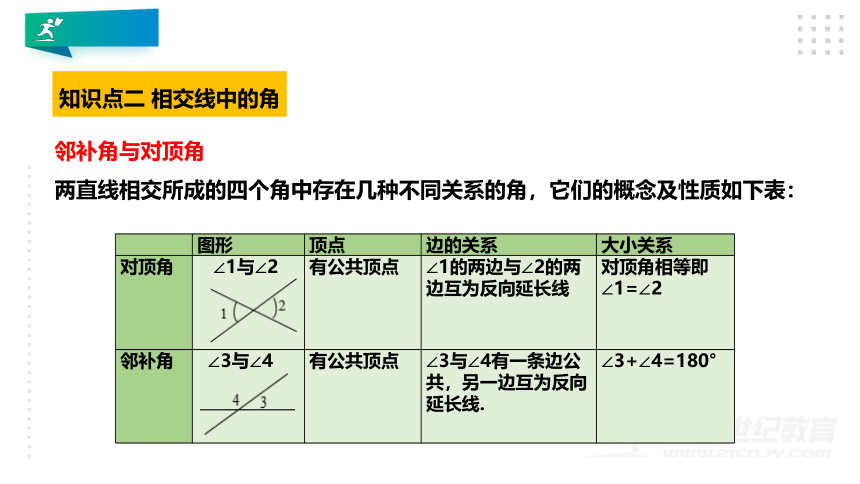
邻补角与对顶角
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}
图形
顶点
边的关系
大小关系
对顶角
∠1与∠2
有公共顶点
∠1的两边与∠2的两边互为反向延长线
对顶角相等即∠1=∠2
邻补角
∠3与∠4
有公共顶点
∠3与∠4有一条边公共,另一边互为反向延长线.
∠3+∠4=180°
知识点二 相交线中的角
注意点:
(1)对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
(2)如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角;
(3)如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角;
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
【典例6】如图,∠1与∠2是对顶角的是( )
A
【典例7】如图,直线AB,CD相交于点O,OE⊥CD,垂足为O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
B
同位角:在两条直线的上方,又在直线EF的同侧,具有这种位置关系的两个角叫同位角。(同旁同侧)
如:∠1和∠5。
内错角:在在两条直线之间,又在直线EF的两侧,具有这种位置关系的两个角叫内错角。(内部异侧)
如:∠3和∠5。
同旁内角:在在两条直线之间,又在直线EF的同侧,具有这种位置关系的两个角叫同旁内角。(同旁内侧)
如:∠3和∠6。
同位角、内错角与同旁内角
三线八角:
指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对,同旁内角有2对。
概念:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示,
如:直线与直线互相平行,记作∥,读作a平行于b。
画法:一落、二靠、三移、四画。
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合
知识点三 平行线
平行公理(唯一性):
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
几何描述 :
∵b∥a,c∥a
∴b∥c
判定方法 1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
平行线的判定
判定方法 2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行
几何符号语言:
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
几何符号语言:
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
判定方法 3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行
平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
【典例8】如图,下列说法中不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠ACE是内错角
C.∠B和∠4是同位角 D.∠3和∠1不是内错角
D
【典例9】如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.∠2=∠4
D
【典例10】如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,
则∠CEF 的度数为( )
A.95° B.105° C.110° D.115°
B
【典例11】如图,直线L1、L2分别与直线L3、L4相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
解:∵∠2=104°, ∴∠5=∠2=104°, ∵∠1=76°, ∴∠1+∠5=180°, ∴直线l1∥l2, ∵∠3=68°, ∴∠6=∠3=68°, ∴∠4=180°?∠6=112°.
∵∠2=104°, ∴∠5=∠2=104°, ∵∠1=76°, ∴∠1+∠5=180°,
∴直线l1∥l2,
∵∠3=68°,
∴∠6=∠3=68°,
∴∠4=180°-∠6=112°
命题的概念:
像这样判断一件事情的语句,叫做命题。
命题的形式:“如果…那么…”。(如果+题设,那么+结论)
真命题的概念:
如果题设成立,那么结论一定成立,这样的命题叫做真命题。
假命题的概念:
如果题设成立,不能保证结论一定成立,这样的命题叫做假命题。
如何说明一个命题是假命题:只需要举出一个反例即可。
知识点四 命题、定理与证明
一个命题的正确性需经过推理,才能作出判断,这个推理过程叫做证明。
证明的依据:可以是已知条件,也可以是学过的定义、基本事实或定理等。
定义、命题、公理和定理之间的关系:
这四者都是句子,都可以判断真假,即定义、公理和定理也是命题,不同的是定义、公理和定理都是真命题,都可以作为进一步判断其他命题真假的依据,而命题不一定是真命题,因而它不一定能作为进一步判断其它命题真假的依据。
证明
【典例12】下列语句是命题的是( )
A.延长线段AB到C B.用量角器画∠AOB=90°
C.同位角相等,两直线平行 D.任何数的平方都不小于0吗?
C
【典例13】命题、定理、基本事实的关系如下:
①基本事实是真命题;②定理是由定义和基本事实推出来的真命题;
③真命题是基本事实;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
知识点五 图形的平移
平移的概念:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移变换 (简称平移),平移不改变物体的形状和大小。
1、把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2、新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
3、连接各组对应点的线段平行且相等。
平移的性质:
作平移图形的一般步骤:
1、确定平移的方向和距离。
2、确定图形的关键点。
3、过这些关键点作与平移方向平行的射线,在射线上截取与平移的距离相等的线段,得到关键点的对应点。
4、依次连接关键点,作出平移后的新图形。
【典例14】下列四个图形中,可以由已知图形(如图)通过平移得到的是( )
D
【典例15】如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知EC=2,BF=8,则平移的距离为________.
3
【典例16】如图,三角形ABC沿BC边所在的直线向右平移得到三角形DEF,下列结论中错误的是( )
A.AC∥DF B.∠A=∠D
C.AC=DF D.EC=CF
D
【典例17】如图,已知直线AB,CD,点P.按要求作垂直:
(1)过点P作AB的,垂足为E;并测量出点P到直线AB的距离.
(2)过点P作CD的垂线PF,垂足为F.
(2)作OM⊥CD,并测量出点O到点P的距离.
解:如图所示.
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下册
直线的位置关系:在同一平面内,不重合的两条直线之间的位置关系只有两种:相交或平行。
知识点一 相交线
【典例1】a、b、c是平面上任意三条直线,交点可以有( ) A.1个或2个或3个 B. 0个或1个或2个或3个 C.1个或2个 D. 都不对
B
概念:当两条相交直线所成的四个角中,有一个角是直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,交点叫做垂足。
表示方法:
如图,a ⊥ b,垂足为O.
记作:a ⊥ b于点O.
垂线
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线的画法:一落、二移、三画。
垂线段最短定理:连接直线外一点与直线上各点的所有线段中,垂线段最短。
【注意事项】
1.线段与线段,线段与射线,线段与直线,射线与射线,射线与直线垂直,是特指它们所在的直线互相垂直。
2.两条直线互相垂直,则它们之间所形成的四个角为直角;若两条直线的夹角为直角,则这两条直线互相垂直。
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
注意:
1.垂线是一条直线,而垂线段是一条线段。
2.经过直线外一点到这条直线的垂线段有且只有一条。
3.经过一点画射线或线段的垂线,是指它们所在直线的垂线,垂足的位置不固定,可能会出现在射线的反向延长线或线段的延长线上。
【典例3】如图,AD为三角形ABC的高,能表示点到直 线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
B
C
D
A
B
【典例2】下列图形中线段PQ的长度表示点P到直线a的距离的是( )
C
【典例4】如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O. (1)请直接写出图中所有与∠AOC相等的角:______. (2)若∠AOD=150°,求∠AOE的度数.
解:(1)∵直线AB,CD相交于点O, ∴∠AOC=∠BOD, ∵OF平分∠AOE, ∴∠AOF=∠EOF, ∵OF⊥CD, ∴∠COF=∠DOF=90°, ∴∠DOE=∠AOC, ∴与∠AOD相等的角有∠BOD,∠DOE,
解:(2)∵OF⊥CD, ∴∠DOF=90°, ∵∠AOD=150°, ∴∠AOF=60°, ∵OF平分∠AOE, ∴∠AOE=2∠AOF=120°.
【典例5】如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O. (1)请直接写出图中所有与∠AOC相等的角:______. (2)若∠AOD=150°,求∠AOE的度数.
邻补角与对顶角
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}
图形
顶点
边的关系
大小关系
对顶角
∠1与∠2
有公共顶点
∠1的两边与∠2的两边互为反向延长线
对顶角相等即∠1=∠2
邻补角
∠3与∠4
有公共顶点
∠3与∠4有一条边公共,另一边互为反向延长线.
∠3+∠4=180°
知识点二 相交线中的角
注意点:
(1)对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
(2)如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角;
(3)如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角;
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
【典例6】如图,∠1与∠2是对顶角的是( )
A
【典例7】如图,直线AB,CD相交于点O,OE⊥CD,垂足为O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
B
同位角:在两条直线的上方,又在直线EF的同侧,具有这种位置关系的两个角叫同位角。(同旁同侧)
如:∠1和∠5。
内错角:在在两条直线之间,又在直线EF的两侧,具有这种位置关系的两个角叫内错角。(内部异侧)
如:∠3和∠5。
同旁内角:在在两条直线之间,又在直线EF的同侧,具有这种位置关系的两个角叫同旁内角。(同旁内侧)
如:∠3和∠6。
同位角、内错角与同旁内角
三线八角:
指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对,同旁内角有2对。
概念:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示,
如:直线与直线互相平行,记作∥,读作a平行于b。
画法:一落、二靠、三移、四画。
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合
知识点三 平行线
平行公理(唯一性):
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
几何描述 :
∵b∥a,c∥a
∴b∥c
判定方法 1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
平行线的判定
判定方法 2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行
几何符号语言:
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
几何符号语言:
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
判定方法 3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行
平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
【典例8】如图,下列说法中不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠ACE是内错角
C.∠B和∠4是同位角 D.∠3和∠1不是内错角
D
【典例9】如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.∠2=∠4
D
【典例10】如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,
则∠CEF 的度数为( )
A.95° B.105° C.110° D.115°
B
【典例11】如图,直线L1、L2分别与直线L3、L4相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
解:∵∠2=104°, ∴∠5=∠2=104°, ∵∠1=76°, ∴∠1+∠5=180°, ∴直线l1∥l2, ∵∠3=68°, ∴∠6=∠3=68°, ∴∠4=180°?∠6=112°.
∵∠2=104°, ∴∠5=∠2=104°, ∵∠1=76°, ∴∠1+∠5=180°,
∴直线l1∥l2,
∵∠3=68°,
∴∠6=∠3=68°,
∴∠4=180°-∠6=112°
命题的概念:
像这样判断一件事情的语句,叫做命题。
命题的形式:“如果…那么…”。(如果+题设,那么+结论)
真命题的概念:
如果题设成立,那么结论一定成立,这样的命题叫做真命题。
假命题的概念:
如果题设成立,不能保证结论一定成立,这样的命题叫做假命题。
如何说明一个命题是假命题:只需要举出一个反例即可。
知识点四 命题、定理与证明
一个命题的正确性需经过推理,才能作出判断,这个推理过程叫做证明。
证明的依据:可以是已知条件,也可以是学过的定义、基本事实或定理等。
定义、命题、公理和定理之间的关系:
这四者都是句子,都可以判断真假,即定义、公理和定理也是命题,不同的是定义、公理和定理都是真命题,都可以作为进一步判断其他命题真假的依据,而命题不一定是真命题,因而它不一定能作为进一步判断其它命题真假的依据。
证明
【典例12】下列语句是命题的是( )
A.延长线段AB到C B.用量角器画∠AOB=90°
C.同位角相等,两直线平行 D.任何数的平方都不小于0吗?
C
【典例13】命题、定理、基本事实的关系如下:
①基本事实是真命题;②定理是由定义和基本事实推出来的真命题;
③真命题是基本事实;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
知识点五 图形的平移
平移的概念:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移变换 (简称平移),平移不改变物体的形状和大小。
1、把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2、新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
3、连接各组对应点的线段平行且相等。
平移的性质:
作平移图形的一般步骤:
1、确定平移的方向和距离。
2、确定图形的关键点。
3、过这些关键点作与平移方向平行的射线,在射线上截取与平移的距离相等的线段,得到关键点的对应点。
4、依次连接关键点,作出平移后的新图形。
【典例14】下列四个图形中,可以由已知图形(如图)通过平移得到的是( )
D
【典例15】如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知EC=2,BF=8,则平移的距离为________.
3
【典例16】如图,三角形ABC沿BC边所在的直线向右平移得到三角形DEF,下列结论中错误的是( )
A.AC∥DF B.∠A=∠D
C.AC=DF D.EC=CF
D
【典例17】如图,已知直线AB,CD,点P.按要求作垂直:
(1)过点P作AB的,垂足为E;并测量出点P到直线AB的距离.
(2)过点P作CD的垂线PF,垂足为F.
(2)作OM⊥CD,并测量出点O到点P的距离.
解:如图所示.
https://www.21cnjy.com/help/help_extract.php
