2021-2022学年人教版数学八年级下册17.2 勾股定理的逆定理 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.2 勾股定理的逆定理 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 389.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 14:59:28 | ||
图片预览






文档简介
(共18张PPT)
17.2 勾股定理的逆定理
教学目标
1、知识与技能目标:
·理解并证明勾股定理的逆命题
·能用勾股定理的逆定理判定直角三角形
·了解逆命题、逆定理、互逆命题、定理及勾股数的概念
2、过程与方法目标:
经历“观察—测量—猜想—论证”的探究过程,体会“构造法”证明数学命题的基本思想
3、情感、态度价值观目标:
培养学生严谨的学习态度
教学重点:
探索并证明勾股定理的逆定理
教学难点:
勾股定理的逆定理的证明过程
教具准备:
PPT课件、套尺、圆规、足够长的棉线
一、创设情境、提出问题
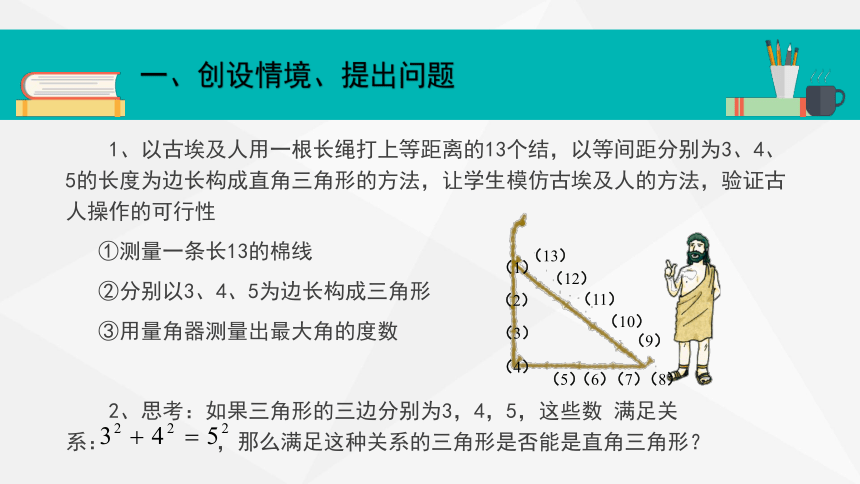
1、以古埃及人用一根长绳打上等距离的13个结,以等间距分别为3、4、5的长度为边长构成直角三角形的方法,让学生模仿古埃及人的方法,验证古人操作的可行性
①测量一条长13的棉线
②分别以3、4、5为边长构成三角形
③用量角器测量出最大角的度数
2、思考:如果三角形的三边分别为3,4,5,这些数 满足关系: ,那么满足这种关系的三角形是否能是直角三角形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
二、精确验证、提出猜想
实验操作:
(1)画一画:下列各组数中的两数平方和等于第三数的
平方,分别以这些数为边长画出三角形(单位:cm),
它们是直角三角形吗?
① 3.5,6,6.5; ② 5,12,13.
(2)量一量:用量角器分别测量上述各三角形的最大角
的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
三、探究验证
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
做法:画一个Rt△A'B'C'使B'C'=a,A'C'=b,∠C '=90°
方法一:剪下△ABC与△A'B'C',重叠,看是否能够重合;
方法二:用推理论证的方法来证明两个三角形全等。
A'
B'
C'
A
B
C
a
b
c
引出概念
1、勾股定理:如果直角三角形两直角边分别为a,b,
斜边为c,那么a2+b2=c2.
2、勾股定理的定理:如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
3、巩固知识并举例
四、应用新知
例1 判断由线段a,b,c 组成的三角形是不是直角三角形:
(1) a=15,b=17,c=8;
(2) a=13,b=15,c=14;
(3) a= ,b=5,c=8.
分析:根据勾股定理及其逆定理判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
概念:像15,17,8 这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
勾股定理的应用练习
活动1
问题1:请叙述出勾股定理的具体内容。
问题2:勾股定理应用的条件有哪些?
活动2
练习:
1.在△ABC中,∠B =90°AB=c,BC=a,AC=b。
⑴若a =9,b =15,则c = ;⑵若a =6,c =8,则b = ;⑶已知a:c =3:4, b =25,求c = 。⑷∠A=30°,若b =5,则c = 。
活动3
问题: 某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,为了安全起见梯子的底部与墙基的距离是2.5米。请问消防队员能否进入三楼灭火?
活动4
问题:一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
B
A
C
D
1m
2m
C
B
A
活动5
问题:做了这两题,大家能否归纳一下应用勾股定理解决实际问题的关键在哪里呢?
活动6
问题:如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
B
D
C
A
O
演练一:暑假到了,小华与父亲外出旅游,他的行李箱长为40cm,宽为30 cm,高为70 cm,一把80 cm的雨伞是否放进这个行李箱中?
演练二:若△ABC的三边a、b、c满足条件
请你判断△ABC的形状.
演练三:我们都知道数轴上的点有的表示有
理数,有的表示无理数,你能在数轴上画出表示
的点吗
演练四葭生池中
今有方池一丈,
葭生其中央,
出水一尺,
引葭赴岸,
适与岸齐。
问:水深、葭长各几何?
5尺
X-1
X
1尺
解:可设葭长为x尺,
则水深为(x-1)尺。
则有: (x-1)2+52=x2
解得:x=13
所以:葭长13尺,水深12尺。
葭(jiā)
本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长
演练五:假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?
C
解:在Rt△ABC中,∠ACB=90°
AC=6,BC=8,根据勾股定理,得
AB =
=
=10(千米)
答:登陆点A到宝藏点B的直线距离是10千米。
过点B作BC⊥AC于C
1、课堂小结:说说这节课你有什么收获?
2、思考题:笨人持竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭。有个邻居聪明者,教他斜竿对两角。笨伯依言试一试,不多不少刚抵足。借问竿长多少数,谁人算出我佩服。
——(当代数学教育家清华大学教授许莼舫著作《古算题味》)
谢谢聆听
17.2 勾股定理的逆定理
教学目标
1、知识与技能目标:
·理解并证明勾股定理的逆命题
·能用勾股定理的逆定理判定直角三角形
·了解逆命题、逆定理、互逆命题、定理及勾股数的概念
2、过程与方法目标:
经历“观察—测量—猜想—论证”的探究过程,体会“构造法”证明数学命题的基本思想
3、情感、态度价值观目标:
培养学生严谨的学习态度
教学重点:
探索并证明勾股定理的逆定理
教学难点:
勾股定理的逆定理的证明过程
教具准备:
PPT课件、套尺、圆规、足够长的棉线
一、创设情境、提出问题
1、以古埃及人用一根长绳打上等距离的13个结,以等间距分别为3、4、5的长度为边长构成直角三角形的方法,让学生模仿古埃及人的方法,验证古人操作的可行性
①测量一条长13的棉线
②分别以3、4、5为边长构成三角形
③用量角器测量出最大角的度数
2、思考:如果三角形的三边分别为3,4,5,这些数 满足关系: ,那么满足这种关系的三角形是否能是直角三角形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
二、精确验证、提出猜想
实验操作:
(1)画一画:下列各组数中的两数平方和等于第三数的
平方,分别以这些数为边长画出三角形(单位:cm),
它们是直角三角形吗?
① 3.5,6,6.5; ② 5,12,13.
(2)量一量:用量角器分别测量上述各三角形的最大角
的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
三、探究验证
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
做法:画一个Rt△A'B'C'使B'C'=a,A'C'=b,∠C '=90°
方法一:剪下△ABC与△A'B'C',重叠,看是否能够重合;
方法二:用推理论证的方法来证明两个三角形全等。
A'
B'
C'
A
B
C
a
b
c
引出概念
1、勾股定理:如果直角三角形两直角边分别为a,b,
斜边为c,那么a2+b2=c2.
2、勾股定理的定理:如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
3、巩固知识并举例
四、应用新知
例1 判断由线段a,b,c 组成的三角形是不是直角三角形:
(1) a=15,b=17,c=8;
(2) a=13,b=15,c=14;
(3) a= ,b=5,c=8.
分析:根据勾股定理及其逆定理判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
概念:像15,17,8 这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
勾股定理的应用练习
活动1
问题1:请叙述出勾股定理的具体内容。
问题2:勾股定理应用的条件有哪些?
活动2
练习:
1.在△ABC中,∠B =90°AB=c,BC=a,AC=b。
⑴若a =9,b =15,则c = ;⑵若a =6,c =8,则b = ;⑶已知a:c =3:4, b =25,求c = 。⑷∠A=30°,若b =5,则c = 。
活动3
问题: 某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,为了安全起见梯子的底部与墙基的距离是2.5米。请问消防队员能否进入三楼灭火?
活动4
问题:一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
B
A
C
D
1m
2m
C
B
A
活动5
问题:做了这两题,大家能否归纳一下应用勾股定理解决实际问题的关键在哪里呢?
活动6
问题:如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
B
D
C
A
O
演练一:暑假到了,小华与父亲外出旅游,他的行李箱长为40cm,宽为30 cm,高为70 cm,一把80 cm的雨伞是否放进这个行李箱中?
演练二:若△ABC的三边a、b、c满足条件
请你判断△ABC的形状.
演练三:我们都知道数轴上的点有的表示有
理数,有的表示无理数,你能在数轴上画出表示
的点吗
演练四葭生池中
今有方池一丈,
葭生其中央,
出水一尺,
引葭赴岸,
适与岸齐。
问:水深、葭长各几何?
5尺
X-1
X
1尺
解:可设葭长为x尺,
则水深为(x-1)尺。
则有: (x-1)2+52=x2
解得:x=13
所以:葭长13尺,水深12尺。
葭(jiā)
本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长
演练五:假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?
C
解:在Rt△ABC中,∠ACB=90°
AC=6,BC=8,根据勾股定理,得
AB =
=
=10(千米)
答:登陆点A到宝藏点B的直线距离是10千米。
过点B作BC⊥AC于C
1、课堂小结:说说这节课你有什么收获?
2、思考题:笨人持竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭。有个邻居聪明者,教他斜竿对两角。笨伯依言试一试,不多不少刚抵足。借问竿长多少数,谁人算出我佩服。
——(当代数学教育家清华大学教授许莼舫著作《古算题味》)
谢谢聆听
