【2022春人教八下数学同步精品课件+变式练习】18.2.1 矩形(第二课时 矩形的判定) 课件(共20张PPT)
文档属性
| 名称 | 【2022春人教八下数学同步精品课件+变式练习】18.2.1 矩形(第二课时 矩形的判定) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 09:57:41 | ||
图片预览







文档简介
(共20张PPT)
数学(人教版)
八年级 下册
18.2.1 矩形
(第二课时 矩形的判定)
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解矩形的判定定理。
2、尝试对矩形判定定理的证明。
3、利用矩形的判定定理解决简单问题。
重点
理解并掌握矩形的判定定理。
难点
利用矩形的判定定理解决简单问题。
矩形的知识点回顾
概念:
注意事项:
矩形的性质:
有一个角是直角的平行四边形叫做矩形,也叫做长方形.
1、矩形是一种特殊的平行四边形。
2、平行四边形不一定是矩形。
矩形的两组对边分别相等
矩形对角线互相平分
矩形的两组对角分别相等
矩形的四个角都是直角
矩形的对角线相等
A
B
D
C
本节课我们学习如何判定一个平行四边形或四边形是矩形
探索与思考
矩形性质的逆命题:
两组对边分别相等的四边形是矩形
两组对角分别相等的四边形是矩形
对角线互相平分的四边形是矩形
四个角都是直角的四边形是矩形
对角线相等的平行四边形是矩形
想一想,矩形性质的逆命题是否成立,请举出反例?
前三个逆命题不一定成立,当条件成立时,结论可能是平行四边形,也可能是矩形。
本节课我们讨论
这两个逆命题是否成立
探索与思考
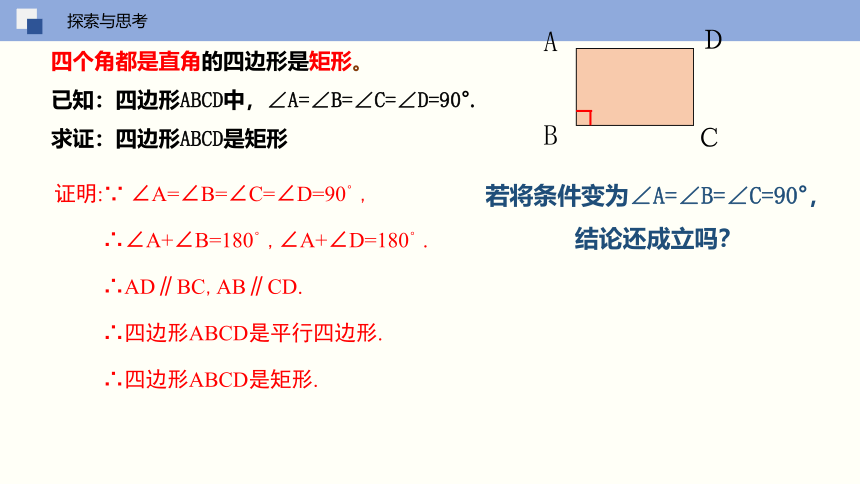
四个角都是直角的四边形是矩形。
已知:四边形ABCD中,∠A=∠B=∠C=∠D=90°.
求证:四边形ABCD是矩形
A
B
D
C
证明:∵ ∠A=∠B=∠C=∠D=90°,
∴∠A+∠B=180°,∠A+∠D=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
若将条件变为∠A=∠B=∠C=90°,
结论还成立吗?
探索与思考
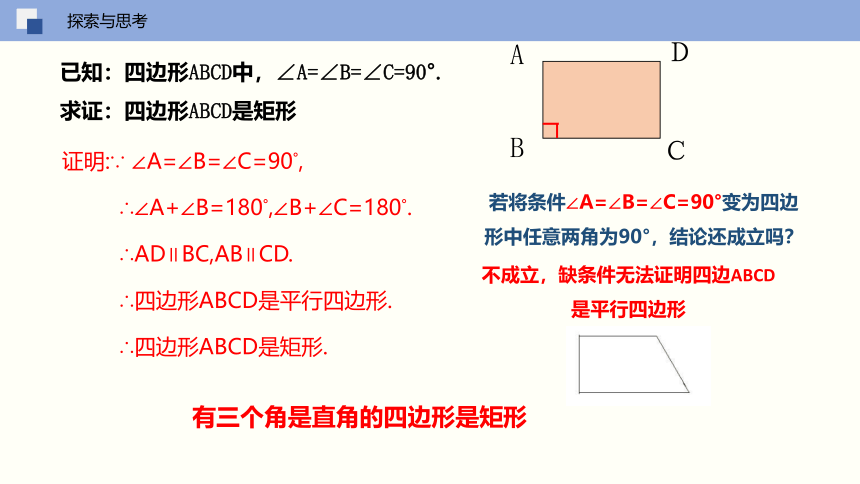
已知:四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形
A
B
D
C
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
若将条件∠A=∠B=∠C=90°变为四边形中任意两角为90°,结论还成立吗?
有三个角是直角的四边形是矩形
不成立,缺条件无法证明四边ABCD是平行四边形
探索与思考
对角线相等的平行四边形是矩形。
已知: ABCD中,AC=BD,
求证:四边形ABCD是矩形。
A
B
D
C
O
证明:∵平行四边形ABCD
∴AB∥CD,AB=CD
∵AB = DC,BC = CB,AC = DB
∴ △ABC≌△DCB(SSS)
∴∠ABC = ∠DCB而AB∥CD,
∴ ∠ABC = 90°,
∴ 四边形ABCD是矩形(矩形的定义).
对角线相等的平行四边形是矩形
理解矩形的判定定理
如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90°
B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO
D.AO=BO=CO=DO
【详解】
A、∠DAB=∠ABC=∠BCD=90°根据有三个角是直角的四边形是矩形可判定为矩形,故此选项错误;
B、AB∥CD,AB=CD,可以判定为平行四边形,又有AB⊥AD,可判定为矩形,故此选项错误;
C、AO=BO,CO=DO,不可以判定为平行四边形,所以不可判定为矩形,故此选项正确;
D、AO=BO=CO=DO,可以得到对角线互相平分且相等,据此可以判定矩形,故此选项错误,故选:C.
理解矩形的判定定理
如图,在 ABCD中,AC、BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )
A.∠BAC=∠ACB B.∠BAC=∠ACD
C.∠BAC=∠DAC D.∠BAC=∠ABD
【详解】根据矩形的判定可知,两条对角线相等的平行四边形是矩形.
所以,假如四边形是矩形,那么AC=BD,
又因为平行四边形对角线互相平分,
所以,AC=BD,
所以,∠BAC=∠ABD.
故只有选项D符合条件。
理解矩形的判定定理
如图,为了检查平行四边形书柜 ABCD 的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线 AC,BD 的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理_____.
【解析】∵平行四边形ABCD的对角线相等,
∴四边形ABCD是矩形,而矩形的四个角都是直角.
理解矩形的判定定理
在数学活动课上,同学们判断一个四边形图案是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( )
A.测量对角线是否平分 B.测量两组对边是否分别相等
C.测量其中三个角是否是直角 D.测量对角线是否相等
【解析】
A、根据对角线互相平分只能得出四边形是平行四边形,故本选项错误;
B、根据对边分别相等,只能得出四边形是平行四边形,故本选项错误;
C、根据矩形的判定,可得出此时四边形是矩形,故本选项正确;
D、根据对角线相等不能得出四边形是矩形,故本选项错误;
故选C.
理解矩形的判定定理
在数学活动课上,老师和同学们判断一块地板砖上的四边形图案是否为矩形,下面是某学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否相等
C.测量对角线是否相等
D.测量对角线是否平分且相等
【详解】
解:A、测量对角线是否互相平分,能判定平行四边形,不能判定矩形,故选项A不符合题意;
B、测量两组对边是否相等,能判定平行四边形,不能判定矩形,故选项B不符合题意;
C、测量对角线是否相等,不能判定平行四边形,也不能判定矩形,故选项C不符合题意;
D、测量对角线是否平分且相等,能判定矩形;
故选:D.
理解矩形的判定定理
如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快___s后,四边形ABPQ成为矩形.
【详解】
设最快x秒,四边形ABPQ成为矩形,
由BP=AQ
得3x=20﹣2x.
解得x=4.
故答案为4
理解矩形的判定定理
如图,为了检验矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
A.AB=CD,AD=BC,AC=BD B.AC=BD,∠B=∠C=90°
C.AB=CD,∠B=∠C=90° D.AB=CD,AC=BD
【解析】
A、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,
∵AC=BD,∴四边形ABCD是矩形,故能判定门框合格;
B、在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL),∴AB=CD,∵∠B=∠C=90°,∴AB∥CD,∴四边形ABCD是平行四边形,∴四边形ABCD是矩形,故能判定门框合格;
C、∵∠B=∠C=90°,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,
∵∠B=∠C=90°,∴四边形ABCD是矩形,故能判定门框合格;
D、当四边形ABCD是等腰梯形时,也满足AB=CD,AC=BD,故不能判定门框合格.故选D.
理解矩形的判定定理
如图,在中,,点、分别是边、的中点,将绕点旋转180°得,则四边形ADCF一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【详解】
点、分别是边、的中点,
,AE=EC
将绕点旋转180°得,
,
,四边形ADCF是平行四边形,
,
,
四边形ADCF是矩形.
故选B
证明四边形是矩形
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=3,BC=4,AC=8。求证:四边形ABCD是矩形.
【详解】
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°,
又∵△ABC中,AB=3,BC=4,AC=5,
∵52=32+42,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
证明四边形是矩形
如图,在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE
求证:四边形BECD是矩形.
【详解】
证明:∵AB=BC,BD平分∠ABC,
∴BD⊥AC,AD=CD.
∵四边形ABED是平行四边形,
∴BE∥AD,BE=AD,
∴四边形BECD是平行四边形.
∵BD⊥AC,∴∠BDC=90°,
∴ BECD是矩形.
课后回顾
理解矩形的判定定理
01
课后回顾
矩形的判定定理的证明
02
利用矩形的判定定理
解决简单问题
03
https://www.21cnjy.com/help/help_extract.php
数学(人教版)
八年级 下册
18.2.1 矩形
(第二课时 矩形的判定)
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解矩形的判定定理。
2、尝试对矩形判定定理的证明。
3、利用矩形的判定定理解决简单问题。
重点
理解并掌握矩形的判定定理。
难点
利用矩形的判定定理解决简单问题。
矩形的知识点回顾
概念:
注意事项:
矩形的性质:
有一个角是直角的平行四边形叫做矩形,也叫做长方形.
1、矩形是一种特殊的平行四边形。
2、平行四边形不一定是矩形。
矩形的两组对边分别相等
矩形对角线互相平分
矩形的两组对角分别相等
矩形的四个角都是直角
矩形的对角线相等
A
B
D
C
本节课我们学习如何判定一个平行四边形或四边形是矩形
探索与思考
矩形性质的逆命题:
两组对边分别相等的四边形是矩形
两组对角分别相等的四边形是矩形
对角线互相平分的四边形是矩形
四个角都是直角的四边形是矩形
对角线相等的平行四边形是矩形
想一想,矩形性质的逆命题是否成立,请举出反例?
前三个逆命题不一定成立,当条件成立时,结论可能是平行四边形,也可能是矩形。
本节课我们讨论
这两个逆命题是否成立
探索与思考
四个角都是直角的四边形是矩形。
已知:四边形ABCD中,∠A=∠B=∠C=∠D=90°.
求证:四边形ABCD是矩形
A
B
D
C
证明:∵ ∠A=∠B=∠C=∠D=90°,
∴∠A+∠B=180°,∠A+∠D=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
若将条件变为∠A=∠B=∠C=90°,
结论还成立吗?
探索与思考
已知:四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形
A
B
D
C
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
若将条件∠A=∠B=∠C=90°变为四边形中任意两角为90°,结论还成立吗?
有三个角是直角的四边形是矩形
不成立,缺条件无法证明四边ABCD是平行四边形
探索与思考
对角线相等的平行四边形是矩形。
已知: ABCD中,AC=BD,
求证:四边形ABCD是矩形。
A
B
D
C
O
证明:∵平行四边形ABCD
∴AB∥CD,AB=CD
∵AB = DC,BC = CB,AC = DB
∴ △ABC≌△DCB(SSS)
∴∠ABC = ∠DCB而AB∥CD,
∴ ∠ABC = 90°,
∴ 四边形ABCD是矩形(矩形的定义).
对角线相等的平行四边形是矩形
理解矩形的判定定理
如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90°
B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO
D.AO=BO=CO=DO
【详解】
A、∠DAB=∠ABC=∠BCD=90°根据有三个角是直角的四边形是矩形可判定为矩形,故此选项错误;
B、AB∥CD,AB=CD,可以判定为平行四边形,又有AB⊥AD,可判定为矩形,故此选项错误;
C、AO=BO,CO=DO,不可以判定为平行四边形,所以不可判定为矩形,故此选项正确;
D、AO=BO=CO=DO,可以得到对角线互相平分且相等,据此可以判定矩形,故此选项错误,故选:C.
理解矩形的判定定理
如图,在 ABCD中,AC、BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )
A.∠BAC=∠ACB B.∠BAC=∠ACD
C.∠BAC=∠DAC D.∠BAC=∠ABD
【详解】根据矩形的判定可知,两条对角线相等的平行四边形是矩形.
所以,假如四边形是矩形,那么AC=BD,
又因为平行四边形对角线互相平分,
所以,AC=BD,
所以,∠BAC=∠ABD.
故只有选项D符合条件。
理解矩形的判定定理
如图,为了检查平行四边形书柜 ABCD 的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线 AC,BD 的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理_____.
【解析】∵平行四边形ABCD的对角线相等,
∴四边形ABCD是矩形,而矩形的四个角都是直角.
理解矩形的判定定理
在数学活动课上,同学们判断一个四边形图案是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( )
A.测量对角线是否平分 B.测量两组对边是否分别相等
C.测量其中三个角是否是直角 D.测量对角线是否相等
【解析】
A、根据对角线互相平分只能得出四边形是平行四边形,故本选项错误;
B、根据对边分别相等,只能得出四边形是平行四边形,故本选项错误;
C、根据矩形的判定,可得出此时四边形是矩形,故本选项正确;
D、根据对角线相等不能得出四边形是矩形,故本选项错误;
故选C.
理解矩形的判定定理
在数学活动课上,老师和同学们判断一块地板砖上的四边形图案是否为矩形,下面是某学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否相等
C.测量对角线是否相等
D.测量对角线是否平分且相等
【详解】
解:A、测量对角线是否互相平分,能判定平行四边形,不能判定矩形,故选项A不符合题意;
B、测量两组对边是否相等,能判定平行四边形,不能判定矩形,故选项B不符合题意;
C、测量对角线是否相等,不能判定平行四边形,也不能判定矩形,故选项C不符合题意;
D、测量对角线是否平分且相等,能判定矩形;
故选:D.
理解矩形的判定定理
如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快___s后,四边形ABPQ成为矩形.
【详解】
设最快x秒,四边形ABPQ成为矩形,
由BP=AQ
得3x=20﹣2x.
解得x=4.
故答案为4
理解矩形的判定定理
如图,为了检验矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
A.AB=CD,AD=BC,AC=BD B.AC=BD,∠B=∠C=90°
C.AB=CD,∠B=∠C=90° D.AB=CD,AC=BD
【解析】
A、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,
∵AC=BD,∴四边形ABCD是矩形,故能判定门框合格;
B、在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL),∴AB=CD,∵∠B=∠C=90°,∴AB∥CD,∴四边形ABCD是平行四边形,∴四边形ABCD是矩形,故能判定门框合格;
C、∵∠B=∠C=90°,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,
∵∠B=∠C=90°,∴四边形ABCD是矩形,故能判定门框合格;
D、当四边形ABCD是等腰梯形时,也满足AB=CD,AC=BD,故不能判定门框合格.故选D.
理解矩形的判定定理
如图,在中,,点、分别是边、的中点,将绕点旋转180°得,则四边形ADCF一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【详解】
点、分别是边、的中点,
,AE=EC
将绕点旋转180°得,
,
,四边形ADCF是平行四边形,
,
,
四边形ADCF是矩形.
故选B
证明四边形是矩形
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=3,BC=4,AC=8。求证:四边形ABCD是矩形.
【详解】
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°,
又∵△ABC中,AB=3,BC=4,AC=5,
∵52=32+42,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
证明四边形是矩形
如图,在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE
求证:四边形BECD是矩形.
【详解】
证明:∵AB=BC,BD平分∠ABC,
∴BD⊥AC,AD=CD.
∵四边形ABED是平行四边形,
∴BE∥AD,BE=AD,
∴四边形BECD是平行四边形.
∵BD⊥AC,∴∠BDC=90°,
∴ BECD是矩形.
课后回顾
理解矩形的判定定理
01
课后回顾
矩形的判定定理的证明
02
利用矩形的判定定理
解决简单问题
03
https://www.21cnjy.com/help/help_extract.php
