【2022春人教八下数学同步精品课件+变式练习】18.2.1 矩形(第一课时 矩形的性质) 课件(共25张PPT)
文档属性
| 名称 | 【2022春人教八下数学同步精品课件+变式练习】18.2.1 矩形(第一课时 矩形的性质) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 09:54:49 | ||
图片预览






文档简介
(共25张PPT)
数学(人教版)
八年级 下册
18.2.3 正方形
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解矩形的概念。
2、探索矩形的性质。
3、理解直角三角形斜边的中线等于斜边的一半。
重点
探索矩形的性质。
难点
能利用矩形的性质解决实际问题。
生活中常见的长方形
想一想,图中的长方形
与平行四边形之间有什么联系吗?
观察与思考
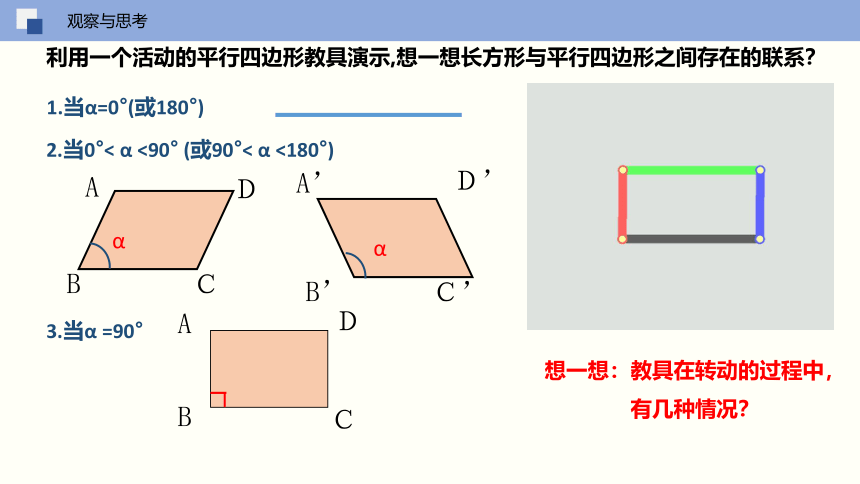
利用一个活动的平行四边形教具演示,想一想长方形与平行四边形之间存在的联系?
A
B
D
C
α
想一想:教具在转动的过程中,
有几种情况?
1.当α=0°(或180°)
2.当0°< α <90° (或90°< α <180°)
A’
B’
D’
C’
α
3.当α =90°
A
B
D
C
矩形
有一个角是直角的平行四边形叫做矩形,也叫做长方形.
【注意】
1、矩形是一种特殊的平行四边形。
2、平行四边形不一定是矩形。
【矩形的条件】①平行四边形;②其中有一个角是直角。
A
B
D
C
因为矩形是特殊的平行四边形,
所以它具有平行四边形的所有性质,
由于它有一个角为直角,
它是否具有一般平行四边形不具有的一些特殊性质呢?
探索与思考
A
B
D
C
A
B
D
C
O
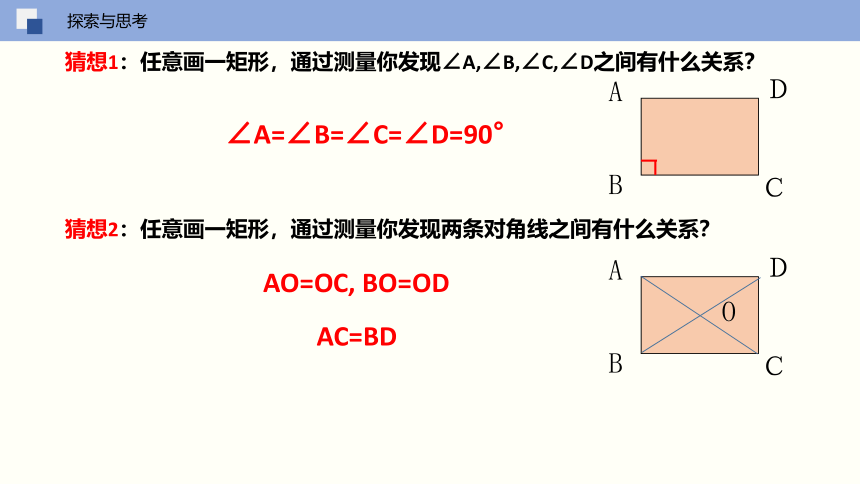
猜想1:任意画一矩形,通过测量你发现∠A,∠B,∠C,∠D之间有什么关系?
猜想2:任意画一矩形,通过测量你发现两条对角线之间有什么关系?
∠A=∠B=∠C=∠D=90°
AO=OC, BO=OD
AC=BD
探索与证明
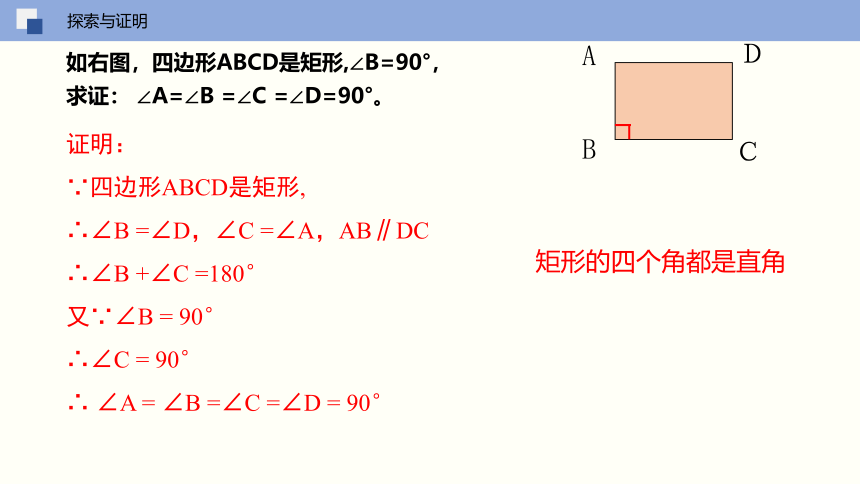
如右图,四边形ABCD是矩形,∠B=90°,
求证: ∠A=∠B =∠C =∠D=90°。
A
B
D
C
证明:
∵四边形ABCD是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC
∴∠B +∠C =180°
又∵∠B = 90°
∴∠C = 90°
∴ ∠A = ∠B =∠C =∠D = 90°
矩形的四个角都是直角
探索与证明
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
D
C
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB
∴△ABC≌△DCB(SAS).
∴AC=DB.
矩形的对角线相等
小结
矩形的性质:
矩形的对边相等
矩形对角线互相平分
矩形的对角相等
A
B
D
C
O
矩形的四个角都是直角
矩形的对角线相等
平行四边形
矩形
矩形既是轴对称,又是中心对称图形
利用矩形的性质求解
如图,矩形ABCD中,,,则AC的长是
A.4 B. C.8 D.10
【详解】
解:∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,∴OA=OB,
∵∠BOC=120°,∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=3,∴AC=2OA=6,故选:B.
利用矩形的性质求解
如图,矩形的对角线AC和BD相交于O,∠BOC=120°,AB=5,则BD的长是_____
【详解】
解:∵∠BOC=120°,
∴∠AOB=180°﹣∠BOC=180°﹣120°=60°,
∵四边形ABCD是矩形,
∴AO=BO=OD,
∴△AOB是等边三角形,
∴AO=OB=AB=5,
∴BD=2OB=10.
利用矩形的性质求解
如图,矩形ABCD的对角线交于点O,若∠BAO=65°,则∠AOD等于( )
A.110° B.115° C.130° D.150°
【详解】
解:∵四边形ABCD是矩形,
∴AC=BD,OA=OB,
∠BAO =∠ABO=65°,
∠AOD =∠BAO+∠ABO = 65°+65°=130°.
故答案为:C
利用矩形的性质求解
如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.
若,,求BF的长.
【详解】
解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC’ = AB = 3,CF = C'F
在Rt△BC'F中,C’F2 = BF2+C'B2,
∴CF2 =(9-CF)2+9
∴CF = 5
∴BF = 4.
利用矩形的性质求解
如图,矩形ABCD的对角线AC=10cm,∠AOD=120°,则AB的长为 cm.
【解析】
∵四边形ABCD是矩形,
∴OA=AC,OB=BD,BD=AC=10cm,
∴OA=OB=5cm,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=5cm.
利用矩形的性质求解
将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,则∠EBD的度数( )
A.80° B.90° C.100° D.110°
【详解】
解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠EBD=∠A′BE+∠DBC′=180°×=90°.
故选B.
利用矩形的性质求解(提高)
已知矩形的面积是4,其中一边长为,则对角线长为___.
直角三角形斜边中线
A
B
C
O
如图,一张矩形纸片,沿着对角线AC剪去一部分,在Rt△ABC中,BO是斜边AC上的中线,思考:AC与BO之间的关系?并尝试证明?
A
B
D
C
O
即:直角三角形斜边上的中线等于斜边的一半
AC
探索与思考
如图,在Rt△ABC中,∠ABC=90°,BO是斜边AC上的中线.
求证: BO = AC
A
B
C
O
D
证明:
延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形
∵∠ABC=90°
∴平行四边形ABCD是矩形,
∴AC=BD,
∴BO = BD= AC.
利用直角三角形斜边中线性质求解
三角形的两直角边长分别为6和8,则斜边上的中线长是( )
A.10 B.2.5 C.5 D.8
【详解】
已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故选:C.
利用直角三角形斜边中线性质求解
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )
A.2 B.3 C.4 D.2
【解析】
∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∴AE=CE=5,
∵AD=2,∴DE=3,
∵CD为AB边上的高,∴在Rt△CDE中,CD=,
故选C.
利用直角三角形斜边中线性质求解
如图,在Rt△ABC中,∠ACB=90°,CD是斜边上的中线,若CD=BC,则∠A=_____.
【详解】
解:如图,∵在Rt△ABC中,∠ACB=90°,CD是斜边上的中线,
∴BD=CD.
又∵CD=BC,
∴CD=BC=BD,
∴△BCD是等边三角形,
∴∠B=60°,
∴∠A=90°﹣∠B=30°.
利用直角三角形斜边中线性质求解
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为3.6km,则M、C两点间的距离为( )
A.1.8km B.3.6km C.3km D.2km
【详解】
解:∵AC⊥BC,
∴∠ACB=90°,
∵M点是AB的中点,AB=3.6km,
∴CM=AB=1.8km.
故选:A.
课后回顾
理解矩形的概念
01
课后回顾
理解矩形的性质
02
理解“直角三角形斜边的中线等于斜边的一半”的性质
03
https://www.21cnjy.com/help/help_extract.php
数学(人教版)
八年级 下册
18.2.3 正方形
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解矩形的概念。
2、探索矩形的性质。
3、理解直角三角形斜边的中线等于斜边的一半。
重点
探索矩形的性质。
难点
能利用矩形的性质解决实际问题。
生活中常见的长方形
想一想,图中的长方形
与平行四边形之间有什么联系吗?
观察与思考
利用一个活动的平行四边形教具演示,想一想长方形与平行四边形之间存在的联系?
A
B
D
C
α
想一想:教具在转动的过程中,
有几种情况?
1.当α=0°(或180°)
2.当0°< α <90° (或90°< α <180°)
A’
B’
D’
C’
α
3.当α =90°
A
B
D
C
矩形
有一个角是直角的平行四边形叫做矩形,也叫做长方形.
【注意】
1、矩形是一种特殊的平行四边形。
2、平行四边形不一定是矩形。
【矩形的条件】①平行四边形;②其中有一个角是直角。
A
B
D
C
因为矩形是特殊的平行四边形,
所以它具有平行四边形的所有性质,
由于它有一个角为直角,
它是否具有一般平行四边形不具有的一些特殊性质呢?
探索与思考
A
B
D
C
A
B
D
C
O
猜想1:任意画一矩形,通过测量你发现∠A,∠B,∠C,∠D之间有什么关系?
猜想2:任意画一矩形,通过测量你发现两条对角线之间有什么关系?
∠A=∠B=∠C=∠D=90°
AO=OC, BO=OD
AC=BD
探索与证明
如右图,四边形ABCD是矩形,∠B=90°,
求证: ∠A=∠B =∠C =∠D=90°。
A
B
D
C
证明:
∵四边形ABCD是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC
∴∠B +∠C =180°
又∵∠B = 90°
∴∠C = 90°
∴ ∠A = ∠B =∠C =∠D = 90°
矩形的四个角都是直角
探索与证明
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
D
C
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB
∴△ABC≌△DCB(SAS).
∴AC=DB.
矩形的对角线相等
小结
矩形的性质:
矩形的对边相等
矩形对角线互相平分
矩形的对角相等
A
B
D
C
O
矩形的四个角都是直角
矩形的对角线相等
平行四边形
矩形
矩形既是轴对称,又是中心对称图形
利用矩形的性质求解
如图,矩形ABCD中,,,则AC的长是
A.4 B. C.8 D.10
【详解】
解:∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,∴OA=OB,
∵∠BOC=120°,∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=3,∴AC=2OA=6,故选:B.
利用矩形的性质求解
如图,矩形的对角线AC和BD相交于O,∠BOC=120°,AB=5,则BD的长是_____
【详解】
解:∵∠BOC=120°,
∴∠AOB=180°﹣∠BOC=180°﹣120°=60°,
∵四边形ABCD是矩形,
∴AO=BO=OD,
∴△AOB是等边三角形,
∴AO=OB=AB=5,
∴BD=2OB=10.
利用矩形的性质求解
如图,矩形ABCD的对角线交于点O,若∠BAO=65°,则∠AOD等于( )
A.110° B.115° C.130° D.150°
【详解】
解:∵四边形ABCD是矩形,
∴AC=BD,OA=OB,
∠BAO =∠ABO=65°,
∠AOD =∠BAO+∠ABO = 65°+65°=130°.
故答案为:C
利用矩形的性质求解
如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.
若,,求BF的长.
【详解】
解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC’ = AB = 3,CF = C'F
在Rt△BC'F中,C’F2 = BF2+C'B2,
∴CF2 =(9-CF)2+9
∴CF = 5
∴BF = 4.
利用矩形的性质求解
如图,矩形ABCD的对角线AC=10cm,∠AOD=120°,则AB的长为 cm.
【解析】
∵四边形ABCD是矩形,
∴OA=AC,OB=BD,BD=AC=10cm,
∴OA=OB=5cm,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=5cm.
利用矩形的性质求解
将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,则∠EBD的度数( )
A.80° B.90° C.100° D.110°
【详解】
解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠EBD=∠A′BE+∠DBC′=180°×=90°.
故选B.
利用矩形的性质求解(提高)
已知矩形的面积是4,其中一边长为,则对角线长为___.
直角三角形斜边中线
A
B
C
O
如图,一张矩形纸片,沿着对角线AC剪去一部分,在Rt△ABC中,BO是斜边AC上的中线,思考:AC与BO之间的关系?并尝试证明?
A
B
D
C
O
即:直角三角形斜边上的中线等于斜边的一半
AC
探索与思考
如图,在Rt△ABC中,∠ABC=90°,BO是斜边AC上的中线.
求证: BO = AC
A
B
C
O
D
证明:
延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形
∵∠ABC=90°
∴平行四边形ABCD是矩形,
∴AC=BD,
∴BO = BD= AC.
利用直角三角形斜边中线性质求解
三角形的两直角边长分别为6和8,则斜边上的中线长是( )
A.10 B.2.5 C.5 D.8
【详解】
已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故选:C.
利用直角三角形斜边中线性质求解
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )
A.2 B.3 C.4 D.2
【解析】
∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∴AE=CE=5,
∵AD=2,∴DE=3,
∵CD为AB边上的高,∴在Rt△CDE中,CD=,
故选C.
利用直角三角形斜边中线性质求解
如图,在Rt△ABC中,∠ACB=90°,CD是斜边上的中线,若CD=BC,则∠A=_____.
【详解】
解:如图,∵在Rt△ABC中,∠ACB=90°,CD是斜边上的中线,
∴BD=CD.
又∵CD=BC,
∴CD=BC=BD,
∴△BCD是等边三角形,
∴∠B=60°,
∴∠A=90°﹣∠B=30°.
利用直角三角形斜边中线性质求解
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为3.6km,则M、C两点间的距离为( )
A.1.8km B.3.6km C.3km D.2km
【详解】
解:∵AC⊥BC,
∴∠ACB=90°,
∵M点是AB的中点,AB=3.6km,
∴CM=AB=1.8km.
故选:A.
课后回顾
理解矩形的概念
01
课后回顾
理解矩形的性质
02
理解“直角三角形斜边的中线等于斜边的一半”的性质
03
https://www.21cnjy.com/help/help_extract.php
