【2022春人教八下数学同步精品课件+变式练习】18.2.2 菱形(第一课时 菱形的性质) 课件(共27张PPT)
文档属性
| 名称 | 【2022春人教八下数学同步精品课件+变式练习】18.2.2 菱形(第一课时 菱形的性质) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 08:40:19 | ||
图片预览







文档简介
(共27张PPT)
数学(人教版)
八年级 下册
18.2.2 菱形
第一课时 菱形的性质
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解菱形的概念。
2、探索菱形的性质。
3、利用菱形的性质解决实际问题。
重点
探索菱形的性质。
难点
能利用菱形的性质解决实际问题。
探索与思考
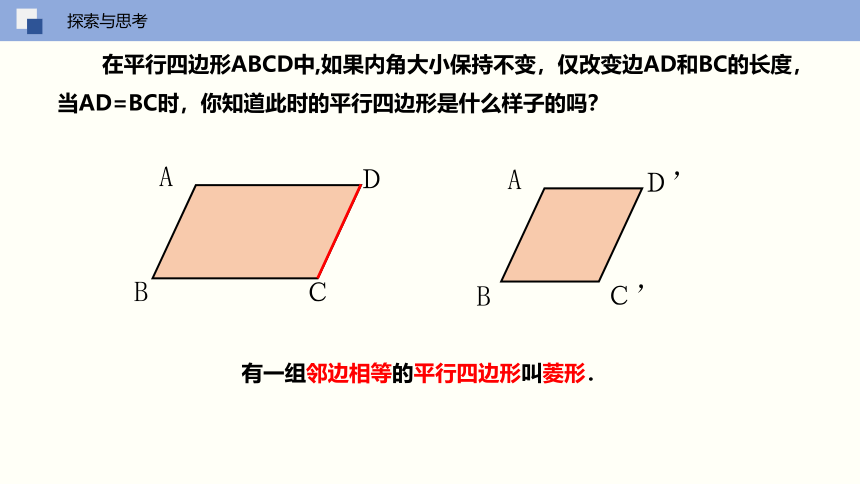
在平行四边形ABCD中,如果内角大小保持不变,仅改变边AD和BC的长度,当AD=BC时,你知道此时的平行四边形是什么样子的吗?
A
B
D
C
A
B
D’
C’
有一组邻边相等的平行四边形叫菱形.
生活中常见的菱形图案
说一说生活中还有那些常见的菱形?
菱形的概念
有一组邻边相等的平行四边形叫做菱形。
【注意事项】
1)菱形是一种特殊的平行四边形。
2)平行四边形不一定是菱形。
【菱形的条件】①平行四边形;②一组邻边相等。
平行四边形
菱形
矩形
平行四边形知识点回顾
平行四边形性质:
平行四边形对边相等
平行四边形对角线互相平分
平行四边形对角相等
因为菱形是特殊的平行四边形,
所以它具有平行四边形的所有性质,
由于它有一组邻边相等,
它是否具有一般平行四边形不具有的一些特殊性质呢?
探索与思考
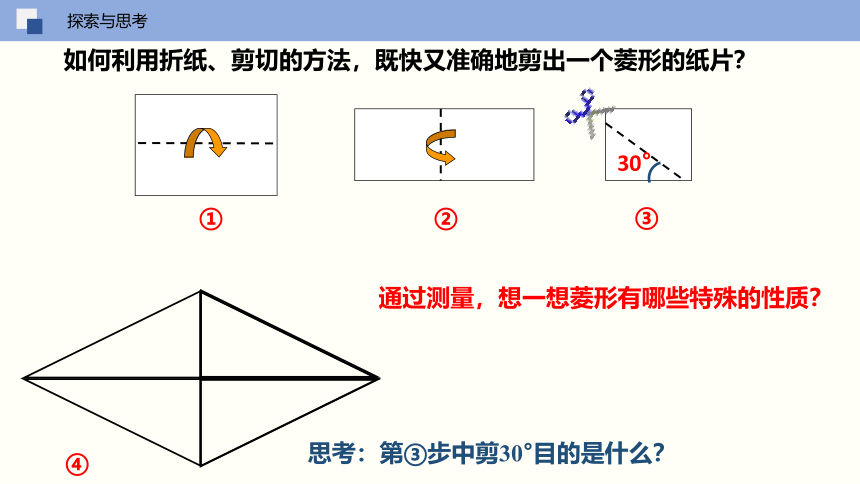
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
30°
通过测量,想一想菱形有哪些特殊的性质?
①
②
③
④
思考:第③步中剪30°目的是什么?
探索菱形的性质
猜想1:测量裁剪后的菱形,你发现AB、BC、CD、AD之间有什么关系?
猜想2:测量裁剪后的菱形,你发现两条对角线之间有什么关系?
AB=BC=CD=AD
AO=OC, BO=OD
A
B
D
C
A
B
D
C
O
AC⊥BD
探索菱形的性质
猜想3:测量裁剪后的菱形,你发现两条对角线与菱形的两组对角之间有什么关系?通过测量填写下表
∠ABD ∠DBC ∠ACB ∠ACD ∠BDC ∠ADB ∠CAD ∠BAC
测量值
对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC,
即每条对角线平分一组对角。
A
B
D
C
O
菱形的性质
菱形的性质:
菱形的对边相等
菱形对角线互相平分
菱形的对角相等
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
平行四边形
菱形
菱形既是轴对称,又是中心对称图形
A
B
D
C
O
练一练
如图,在 ABCD中,AB=AD,对角线AC与BD相交于点O,
求证: 1)AB=BC=CD=AD; 2)AC⊥BD;
3)对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC
A
B
C
O
D
证明:1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC
又∵AB=AD,
∴AB = BC = CD =AD
练一练
如图,在 ABCD中,AB=AD,对角线AC与BD相交于点O,
求证: 1)AB=BC=CD=AD; 2)AC⊥BD;
3)对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC
A
B
C
O
D
2)∵AB = AD
∴△ABD是等腰三角形.
∵四边形ABCD是平行四边形
∴OB = OD
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA, ∠ADB=∠CDB,∠ABD=∠CBD
探索菱形的面积与对角线的关系
菱形是特殊的平行四边形,能否利用它的性质计算菱形ABCD的面积
A
B
C
D
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
=AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
利用菱形的性质解决实际问题
如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
A
B
C
D
O
解:∵花坛ABCD是菱形
∴AC⊥BD,∠ABO= ∠ABC=30°
在Rt ABO中,AO= AB=10
∴BO==10 m
AC=2AO=20 m,BD=2BO=10≈34.64 m
S菱形ABCD =4S△ABO = AC·BD =200≈316.4 ㎡
利用菱形的性质进行计算
如图,在菱形ABCD中,AE⊥BC于E,,AC,则菱形ABCD的周长是
A.6 B.10 C.12 D.16
【详解】
如图连接AC,
C, AE⊥BC
,
菱形ABCD的周长,
故选D.
利用菱形的性质进行计算
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AD等于( )
A.5 B.10 C. D.18
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵AC=8,BD=6,
∴OA=4,OB=3,
∴AB==5,
即菱形ABCD的边长是5.故选A.
利用菱形的性质进行计算
如图,菱形ABCD中,对角线AC,BD相交于点O,点M是DC的中点.若菱形ABCD的周长为24,则的长为( )
A.12 B.8 C.6 D.3
【详解】
解:∵四边形ABCD是菱形,
∴,AC⊥BD,
∵菱形ABCD的周长为24,
∴,
又∵点M是CD中点,
∴,
故选:D.
利用菱形的性质进行计算
在菱形ABCD中,对角线AC,BD相交于点O,如果AC=6,BD=8,那么菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
【详解】解:菱形ABCD的面积===24,故选:C.
利用菱形的性质进行计算
已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.7.2cm D.9.6cm
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB=,
∵菱形ABCD的面积=AB DE=AC BD=×8×6=24,
∴DE= =4.8;
故选B.
利用菱形的性质进行计算(求周长)
如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=4,那么菱形ABCD的周长为( )
A.32 B.24 C.16 D.8
【详解】∵E是AC中点,
∵EF∥BC,交AB于点F,
∴EF是△ABC的中位线,
∴BC=2EF=2×4=8,
∴菱形ABCD的周长是4×8=32,
故选A.
利用菱形的性质进行计算(求周长)
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
1)证明:四边形ACDE是平行四边形;
2)若AC=8,BD=6,求△ADE的周长.
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°,
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5,
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△ADE的周长为AD+AE+DE=5+5+8=18.
利用菱形的性质进行计算(求面积)
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
A.18 B.18 C.24 D.2
【解析】
过点A作AE⊥BC于E
∵在菱形ABCD中,AB=6,∠ABD=30°,
∴∠BAE=30°,
∵AE⊥BC,
∴AE=,
∴菱形ABCD的面积是=,故选B.
利用菱形的性质进行计算(求面积)
在菱形ABCD中,∠ABC∠BAD的度数比为1:2,周长是8cm。
问题:1)两条对角线的长度;2)菱形的面积。
A
B
C
D
解:1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=60°,∠ABO=30°
∴△ABC是等边三角形。则AC=AB
∵菱形ABCD的周长是8cm.∴AB=AC=2cm
∴在Rt ABO中,AO= AB=1 cm
∴BO== cm∴AC=2 cm,BD= cm
2)S菱形ABCD =4S△ABO = AC·BD = 2· = c㎡
菱形中的相关计算通常转化为直角三角形或等腰三角形,
当菱形中有一个角是60°时,
菱形被分为以60°为顶角的两个等边三角形
利用菱形的性质进行计算(求面积)
菱形的周长为100 cm,一条对角线长为14 cm,它的面积是( )
A.168 cm2 B.336 cm2
C.672 cm2 D.84 cm2
【详解】
四边形是菱形,,
,
,
在中,
菱形的面积,故选B
课后回顾
理解菱形的概念
01
课后回顾
理解菱形的性质
02
利用菱形的性质解决
实际问题
03
https://www.21cnjy.com/help/help_extract.php
数学(人教版)
八年级 下册
18.2.2 菱形
第一课时 菱形的性质
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解菱形的概念。
2、探索菱形的性质。
3、利用菱形的性质解决实际问题。
重点
探索菱形的性质。
难点
能利用菱形的性质解决实际问题。
探索与思考
在平行四边形ABCD中,如果内角大小保持不变,仅改变边AD和BC的长度,当AD=BC时,你知道此时的平行四边形是什么样子的吗?
A
B
D
C
A
B
D’
C’
有一组邻边相等的平行四边形叫菱形.
生活中常见的菱形图案
说一说生活中还有那些常见的菱形?
菱形的概念
有一组邻边相等的平行四边形叫做菱形。
【注意事项】
1)菱形是一种特殊的平行四边形。
2)平行四边形不一定是菱形。
【菱形的条件】①平行四边形;②一组邻边相等。
平行四边形
菱形
矩形
平行四边形知识点回顾
平行四边形性质:
平行四边形对边相等
平行四边形对角线互相平分
平行四边形对角相等
因为菱形是特殊的平行四边形,
所以它具有平行四边形的所有性质,
由于它有一组邻边相等,
它是否具有一般平行四边形不具有的一些特殊性质呢?
探索与思考
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
30°
通过测量,想一想菱形有哪些特殊的性质?
①
②
③
④
思考:第③步中剪30°目的是什么?
探索菱形的性质
猜想1:测量裁剪后的菱形,你发现AB、BC、CD、AD之间有什么关系?
猜想2:测量裁剪后的菱形,你发现两条对角线之间有什么关系?
AB=BC=CD=AD
AO=OC, BO=OD
A
B
D
C
A
B
D
C
O
AC⊥BD
探索菱形的性质
猜想3:测量裁剪后的菱形,你发现两条对角线与菱形的两组对角之间有什么关系?通过测量填写下表
∠ABD ∠DBC ∠ACB ∠ACD ∠BDC ∠ADB ∠CAD ∠BAC
测量值
对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC,
即每条对角线平分一组对角。
A
B
D
C
O
菱形的性质
菱形的性质:
菱形的对边相等
菱形对角线互相平分
菱形的对角相等
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
平行四边形
菱形
菱形既是轴对称,又是中心对称图形
A
B
D
C
O
练一练
如图,在 ABCD中,AB=AD,对角线AC与BD相交于点O,
求证: 1)AB=BC=CD=AD; 2)AC⊥BD;
3)对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC
A
B
C
O
D
证明:1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC
又∵AB=AD,
∴AB = BC = CD =AD
练一练
如图,在 ABCD中,AB=AD,对角线AC与BD相交于点O,
求证: 1)AB=BC=CD=AD; 2)AC⊥BD;
3)对角线AC平分∠BAD和∠BCD,对角线BD平分∠ABC和∠ADC
A
B
C
O
D
2)∵AB = AD
∴△ABD是等腰三角形.
∵四边形ABCD是平行四边形
∴OB = OD
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA, ∠ADB=∠CDB,∠ABD=∠CBD
探索菱形的面积与对角线的关系
菱形是特殊的平行四边形,能否利用它的性质计算菱形ABCD的面积
A
B
C
D
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
=AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
利用菱形的性质解决实际问题
如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
A
B
C
D
O
解:∵花坛ABCD是菱形
∴AC⊥BD,∠ABO= ∠ABC=30°
在Rt ABO中,AO= AB=10
∴BO==10 m
AC=2AO=20 m,BD=2BO=10≈34.64 m
S菱形ABCD =4S△ABO = AC·BD =200≈316.4 ㎡
利用菱形的性质进行计算
如图,在菱形ABCD中,AE⊥BC于E,,AC,则菱形ABCD的周长是
A.6 B.10 C.12 D.16
【详解】
如图连接AC,
C, AE⊥BC
,
菱形ABCD的周长,
故选D.
利用菱形的性质进行计算
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AD等于( )
A.5 B.10 C. D.18
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵AC=8,BD=6,
∴OA=4,OB=3,
∴AB==5,
即菱形ABCD的边长是5.故选A.
利用菱形的性质进行计算
如图,菱形ABCD中,对角线AC,BD相交于点O,点M是DC的中点.若菱形ABCD的周长为24,则的长为( )
A.12 B.8 C.6 D.3
【详解】
解:∵四边形ABCD是菱形,
∴,AC⊥BD,
∵菱形ABCD的周长为24,
∴,
又∵点M是CD中点,
∴,
故选:D.
利用菱形的性质进行计算
在菱形ABCD中,对角线AC,BD相交于点O,如果AC=6,BD=8,那么菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
【详解】解:菱形ABCD的面积===24,故选:C.
利用菱形的性质进行计算
已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.7.2cm D.9.6cm
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB=,
∵菱形ABCD的面积=AB DE=AC BD=×8×6=24,
∴DE= =4.8;
故选B.
利用菱形的性质进行计算(求周长)
如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=4,那么菱形ABCD的周长为( )
A.32 B.24 C.16 D.8
【详解】∵E是AC中点,
∵EF∥BC,交AB于点F,
∴EF是△ABC的中位线,
∴BC=2EF=2×4=8,
∴菱形ABCD的周长是4×8=32,
故选A.
利用菱形的性质进行计算(求周长)
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
1)证明:四边形ACDE是平行四边形;
2)若AC=8,BD=6,求△ADE的周长.
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°,
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5,
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△ADE的周长为AD+AE+DE=5+5+8=18.
利用菱形的性质进行计算(求面积)
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
A.18 B.18 C.24 D.2
【解析】
过点A作AE⊥BC于E
∵在菱形ABCD中,AB=6,∠ABD=30°,
∴∠BAE=30°,
∵AE⊥BC,
∴AE=,
∴菱形ABCD的面积是=,故选B.
利用菱形的性质进行计算(求面积)
在菱形ABCD中,∠ABC∠BAD的度数比为1:2,周长是8cm。
问题:1)两条对角线的长度;2)菱形的面积。
A
B
C
D
解:1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=60°,∠ABO=30°
∴△ABC是等边三角形。则AC=AB
∵菱形ABCD的周长是8cm.∴AB=AC=2cm
∴在Rt ABO中,AO= AB=1 cm
∴BO== cm∴AC=2 cm,BD= cm
2)S菱形ABCD =4S△ABO = AC·BD = 2· = c㎡
菱形中的相关计算通常转化为直角三角形或等腰三角形,
当菱形中有一个角是60°时,
菱形被分为以60°为顶角的两个等边三角形
利用菱形的性质进行计算(求面积)
菱形的周长为100 cm,一条对角线长为14 cm,它的面积是( )
A.168 cm2 B.336 cm2
C.672 cm2 D.84 cm2
【详解】
四边形是菱形,,
,
,
在中,
菱形的面积,故选B
课后回顾
理解菱形的概念
01
课后回顾
理解菱形的性质
02
利用菱形的性质解决
实际问题
03
https://www.21cnjy.com/help/help_extract.php
