【2022春人教八下数学同步精品课件+变式练习】18.2.3 正方形 课件(共24张PPT)
文档属性
| 名称 | 【2022春人教八下数学同步精品课件+变式练习】18.2.3 正方形 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
数学(人教版)
八年级 下册
18.2.3 正方形
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解正方形的概念。
2、探索正方形的性质。
3、利用正方形的性质解决实际问题。
重点
探索正方形的性质。
难点
能利用正方形的性质解决实际问题。
生活中常见的正方形
说一说生活中还有那些类似图形?
探索与思考
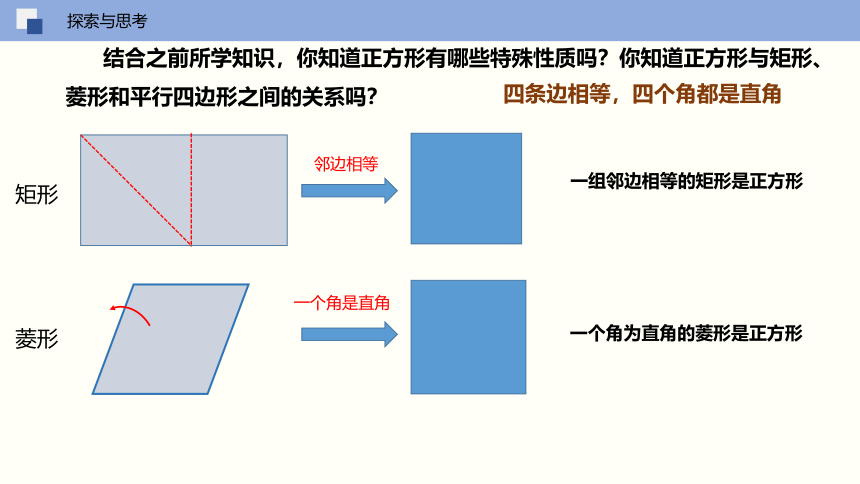
结合之前所学知识,你知道正方形有哪些特殊性质吗?你知道正方形与矩形、菱形和平行四边形之间的关系吗?
四条边相等,四个角都是直角
矩形
邻边相等
一组邻边相等的矩形是正方形
菱形
一个角是直角
一个角为直角的菱形是正方形
正方形
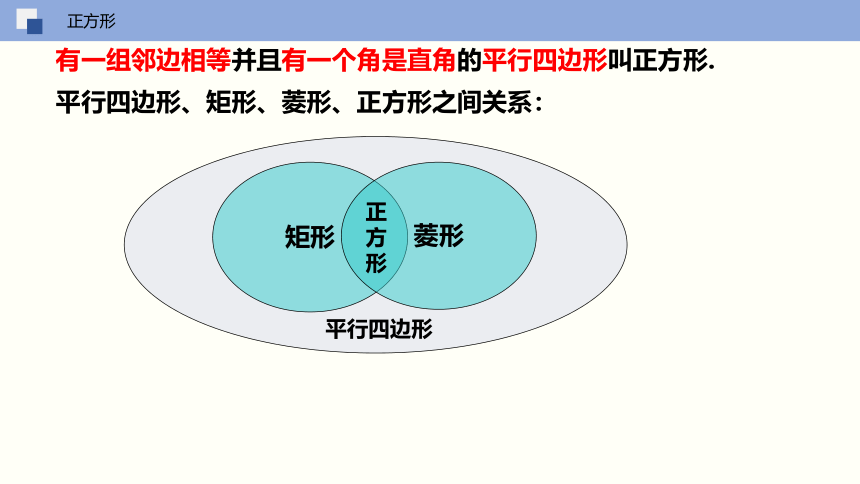
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正
方
形
平行四边形
正方形的性质
正方形的性质:
1、正方形具有平行四边形和菱形的所有性质;
2、正方形的四个角都是直角,四条边都相等;
3、正方形对边平行且相等;
4、正方形的对角线互相垂直平分且相等,对角线平分对角;
5、正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6、正方形既是中心对称图形,也是轴对称图形。
探索与思考
正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O。
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形。
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO
正方形的判定
正方形的判定:
1)有一个角是直角的菱形是正方形;
2)对角线相等的菱形是正方形;
3)一组邻边相等的矩形是正方形;
4)对角线互相垂直的矩形是正方形;
5)对角线互相垂直平分且相等的四边形是正方形;
6)四条边都相等,四个角都是直角的四边形是正方形。
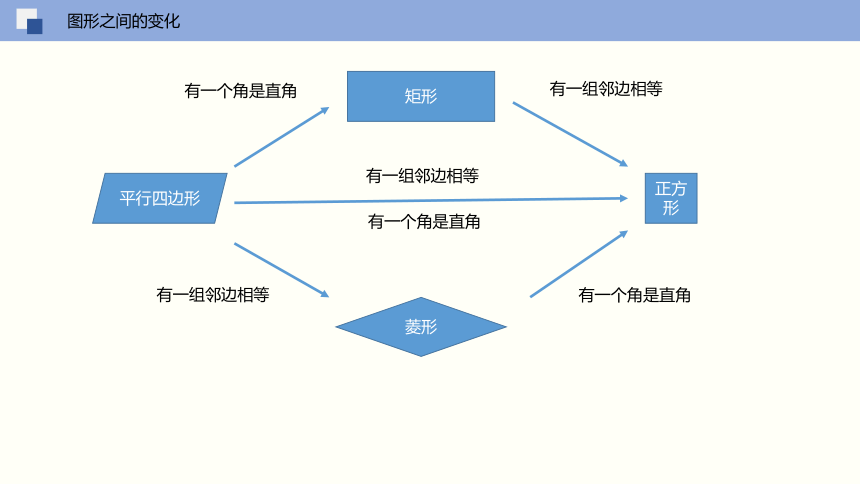
图形之间的变化
平行四边形
矩形
正方形
菱形
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等
有一个角是直角
课堂测试(理解正方形的性质)
对正方形的描述错误的是( )
A.正方形的四个角都是直角 B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形 D.对角线相等的平行四边形是正方形
【详解】
解:∵正方形的四个角都是直角,对角线互相垂直,∴A、B正确;
∵邻边相等的矩形是正方形,∴C正确;
∵对角线相等的平行四边形是矩形,不一定是正方形,∴D不正确;
故选D.
课堂测试(理解正方形的性质)
正方形具有而菱形不一定具有的性质是 ( )
A.对角线相等 B.对角线互相垂直平分
C.四条边相等 D.对角线平分一组对角
【详解】
解:正方形的对角线相等,菱形的对角线不相等,故A符合题意;
正方形和菱形的对角线都互相垂直平分,故B不符合题意;
正方形和菱形的四条边都相等,故C不符合题意;
正方形和菱形的对角线都平分一组对角,故D不符合题意,
故选:A.
课堂测试(理解正方形的性质)
平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
【详解】
解:A. 平行四边形、矩形、菱形、正方形的对角线互相平分,故符合题意;
B. 菱形、正方形的对角线互相垂直,而平行四边形、矩形对角线不互相垂直,故不符合题意;
C. 矩形、正方形的对角线相等,而平行四边形、菱形的对角线不相等,故不符合题意;
D.正方形的对角线互相垂直平分且相等,而平行四边形、矩形、菱形不具有这一性质,故不符合题意.故选:A.
课堂测试(理解正方形的性质)
如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
【解析】
∵将长方形纸片折叠,A落在BC上的F处,∴BA=BF,
∵折痕为BE,沿EF剪下,∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.故选A.
课堂测试(利用正方形的性质进行计算)
如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.52 B.68
C.76 D.86
【解析】
∵∠AEB=90°,AE=6,BE=8,
∴根据勾股定理得AB=10
∴S阴影部分=S正方形ABCD-SRt△ABE=76.
故选C.
课堂测试(利用正方形的性质进行计算)
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
A.2a2 B.4a2 C.6a2 D.8a2
【提示】
正多边形和圆,等腰直角三角形的性质,正方形的性质.图案中间的阴影部分是正方形,面积是,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为的正方形的一半,它的面积用对角线积的一半
【详解】
解:.
故选A.
课堂测试(利用正方形的性质进行计算)
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
【详解】
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
故选:.
课堂测试(利用正方形的性质进行计算)
如图,在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
A.16- B.-12+
C.12- D.4-
【详解】
∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为4cm,cm,
∴AB=4cm,BC= cm,
∴空白部分的面积=×4 12 16=+16 12 16= cm2.
故选B.
利用正方形的性质进行计算
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长____cm.
【解析】
因为正方形AECF的面积为50cm2,
所以
因为菱形ABCD的面积为120cm2,
所以
所以菱形的边长
故答案为13.
利用正方形的性质进行计算
如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
课堂测试(正方形的判定)
已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
【详解】
解:四边形是平行四边形,
A、当时,它是菱形,选项不符合题意,
B、当时,它是菱形,选项不符合题意,
C、当时,它是矩形,选项不符合题意,
D、当AC=BD时,它是矩形,不一定是正方形,选项符合题意,
故选:.
课堂测试(正方形的判定)
下列关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC=BD,则 ABCD是矩形
C.若AC平分∠BAD,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是正方形
【详解】
解:∵ ABCD中,AB⊥BC,∴四边形ABCD是矩形,不一定是菱形,选项A不符合题意;
∵ ABCD中,AC=BD,∴四边形ABCD是矩形,选项B符合题意;
∵ ABCD中,AC平分∠BAD,∴四边形ABCD是菱形,不一定是正方形,选项C不符合题意;
∵ ABCD中,AC⊥BD,∴四边形ABCD是菱形,选项D不符合题意;
故选:B.
课后回顾
理解正方形的概念
01
课后回顾
理解正方形的性质
02
理解正方形的判定
03
https://www.21cnjy.com/help/help_extract.php
数学(人教版)
八年级 下册
18.2.3 正方形
第十八章 平行四边形
2022春人教版七下数学同步精品教学课件
学习目标
学习目标
1、理解正方形的概念。
2、探索正方形的性质。
3、利用正方形的性质解决实际问题。
重点
探索正方形的性质。
难点
能利用正方形的性质解决实际问题。
生活中常见的正方形
说一说生活中还有那些类似图形?
探索与思考
结合之前所学知识,你知道正方形有哪些特殊性质吗?你知道正方形与矩形、菱形和平行四边形之间的关系吗?
四条边相等,四个角都是直角
矩形
邻边相等
一组邻边相等的矩形是正方形
菱形
一个角是直角
一个角为直角的菱形是正方形
正方形
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正
方
形
平行四边形
正方形的性质
正方形的性质:
1、正方形具有平行四边形和菱形的所有性质;
2、正方形的四个角都是直角,四条边都相等;
3、正方形对边平行且相等;
4、正方形的对角线互相垂直平分且相等,对角线平分对角;
5、正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6、正方形既是中心对称图形,也是轴对称图形。
探索与思考
正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O。
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形。
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO
正方形的判定
正方形的判定:
1)有一个角是直角的菱形是正方形;
2)对角线相等的菱形是正方形;
3)一组邻边相等的矩形是正方形;
4)对角线互相垂直的矩形是正方形;
5)对角线互相垂直平分且相等的四边形是正方形;
6)四条边都相等,四个角都是直角的四边形是正方形。
图形之间的变化
平行四边形
矩形
正方形
菱形
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等
有一个角是直角
课堂测试(理解正方形的性质)
对正方形的描述错误的是( )
A.正方形的四个角都是直角 B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形 D.对角线相等的平行四边形是正方形
【详解】
解:∵正方形的四个角都是直角,对角线互相垂直,∴A、B正确;
∵邻边相等的矩形是正方形,∴C正确;
∵对角线相等的平行四边形是矩形,不一定是正方形,∴D不正确;
故选D.
课堂测试(理解正方形的性质)
正方形具有而菱形不一定具有的性质是 ( )
A.对角线相等 B.对角线互相垂直平分
C.四条边相等 D.对角线平分一组对角
【详解】
解:正方形的对角线相等,菱形的对角线不相等,故A符合题意;
正方形和菱形的对角线都互相垂直平分,故B不符合题意;
正方形和菱形的四条边都相等,故C不符合题意;
正方形和菱形的对角线都平分一组对角,故D不符合题意,
故选:A.
课堂测试(理解正方形的性质)
平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
【详解】
解:A. 平行四边形、矩形、菱形、正方形的对角线互相平分,故符合题意;
B. 菱形、正方形的对角线互相垂直,而平行四边形、矩形对角线不互相垂直,故不符合题意;
C. 矩形、正方形的对角线相等,而平行四边形、菱形的对角线不相等,故不符合题意;
D.正方形的对角线互相垂直平分且相等,而平行四边形、矩形、菱形不具有这一性质,故不符合题意.故选:A.
课堂测试(理解正方形的性质)
如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
【解析】
∵将长方形纸片折叠,A落在BC上的F处,∴BA=BF,
∵折痕为BE,沿EF剪下,∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.故选A.
课堂测试(利用正方形的性质进行计算)
如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.52 B.68
C.76 D.86
【解析】
∵∠AEB=90°,AE=6,BE=8,
∴根据勾股定理得AB=10
∴S阴影部分=S正方形ABCD-SRt△ABE=76.
故选C.
课堂测试(利用正方形的性质进行计算)
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
A.2a2 B.4a2 C.6a2 D.8a2
【提示】
正多边形和圆,等腰直角三角形的性质,正方形的性质.图案中间的阴影部分是正方形,面积是,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为的正方形的一半,它的面积用对角线积的一半
【详解】
解:.
故选A.
课堂测试(利用正方形的性质进行计算)
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
【详解】
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
故选:.
课堂测试(利用正方形的性质进行计算)
如图,在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
A.16- B.-12+
C.12- D.4-
【详解】
∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为4cm,cm,
∴AB=4cm,BC= cm,
∴空白部分的面积=×4 12 16=+16 12 16= cm2.
故选B.
利用正方形的性质进行计算
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长____cm.
【解析】
因为正方形AECF的面积为50cm2,
所以
因为菱形ABCD的面积为120cm2,
所以
所以菱形的边长
故答案为13.
利用正方形的性质进行计算
如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
课堂测试(正方形的判定)
已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
【详解】
解:四边形是平行四边形,
A、当时,它是菱形,选项不符合题意,
B、当时,它是菱形,选项不符合题意,
C、当时,它是矩形,选项不符合题意,
D、当AC=BD时,它是矩形,不一定是正方形,选项符合题意,
故选:.
课堂测试(正方形的判定)
下列关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC=BD,则 ABCD是矩形
C.若AC平分∠BAD,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是正方形
【详解】
解:∵ ABCD中,AB⊥BC,∴四边形ABCD是矩形,不一定是菱形,选项A不符合题意;
∵ ABCD中,AC=BD,∴四边形ABCD是矩形,选项B符合题意;
∵ ABCD中,AC平分∠BAD,∴四边形ABCD是菱形,不一定是正方形,选项C不符合题意;
∵ ABCD中,AC⊥BD,∴四边形ABCD是菱形,选项D不符合题意;
故选:B.
课后回顾
理解正方形的概念
01
课后回顾
理解正方形的性质
02
理解正方形的判定
03
https://www.21cnjy.com/help/help_extract.php
