北师大版五年级下册数学第八单元 数据的表示和分析 单元综合练习试卷(word版,含解析)
文档属性
| 名称 | 北师大版五年级下册数学第八单元 数据的表示和分析 单元综合练习试卷(word版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 20:09:22 | ||
图片预览


文档简介
北师大版五年级年级下 八 数据的表示和分析 单元综合练
一、选择题
1.单式折线统计图和复式折线统计图的区别是( )
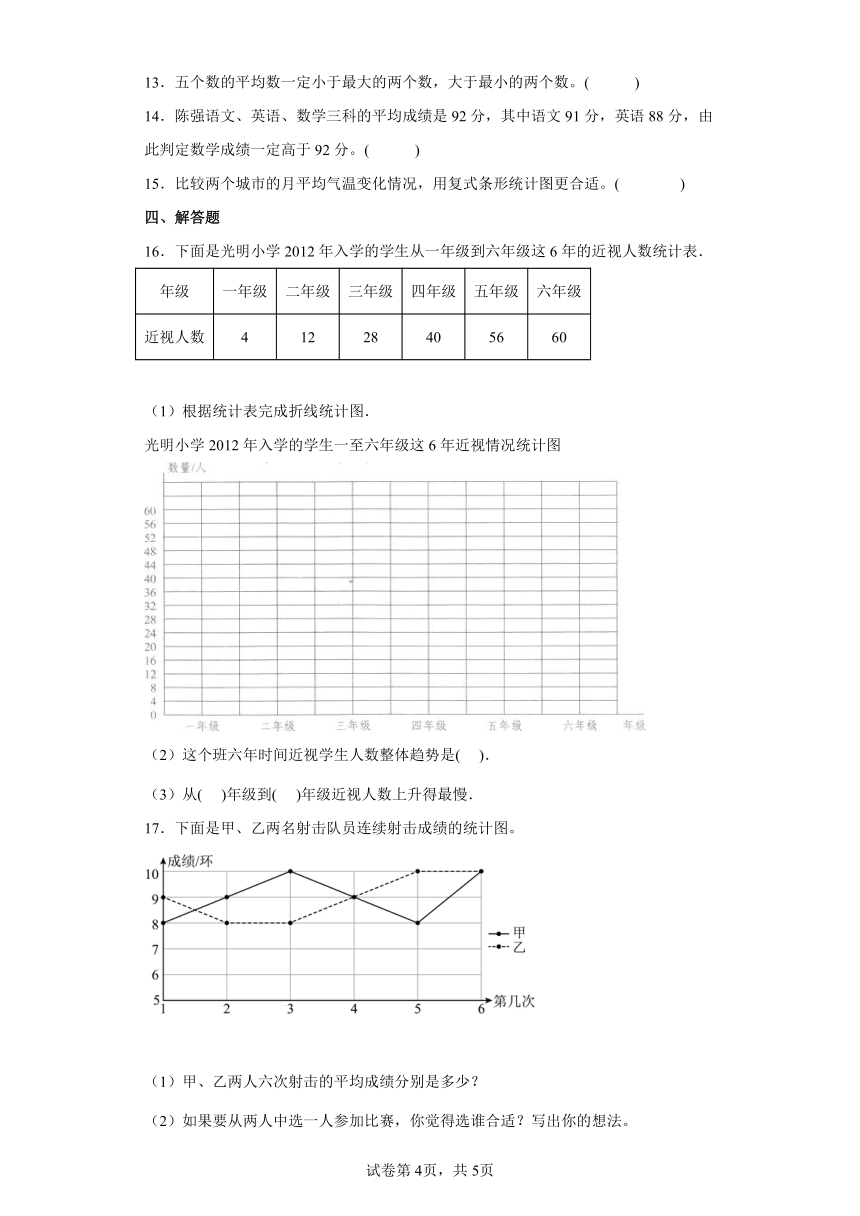
A.单式折线统计图表示出数量的多少,复式折线统计图能反映出数据的变化情况.
B.单式折线统计图比较简单,复式折线统计图不容易看懂.
C.单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示出两组或两组以上的数据的增减变化情况.
2.一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游去,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图像,若不计转向时间,则从开始起到3分钟止他们相遇的次数为( )
A.2次 B.3次 C.4次 D.5次
3.8名同学用软尺测量同一个圆的周长,测量结果如下表:
学号 1 2 3 4 5 6 7 8
周长/cm 9.1 8.9 9.0 9.2 9.1 14.8 9.1 9.03
如果想尽可能减小误差,得到这个圆的周长,你会建议他们选择( )方法。A.采用出现次数最多的9.1 B.去掉14.8把剩余的7个数据加起来除以7
C.把8个数据加起来除以8 D.选择小数点后有两位小数的9.03
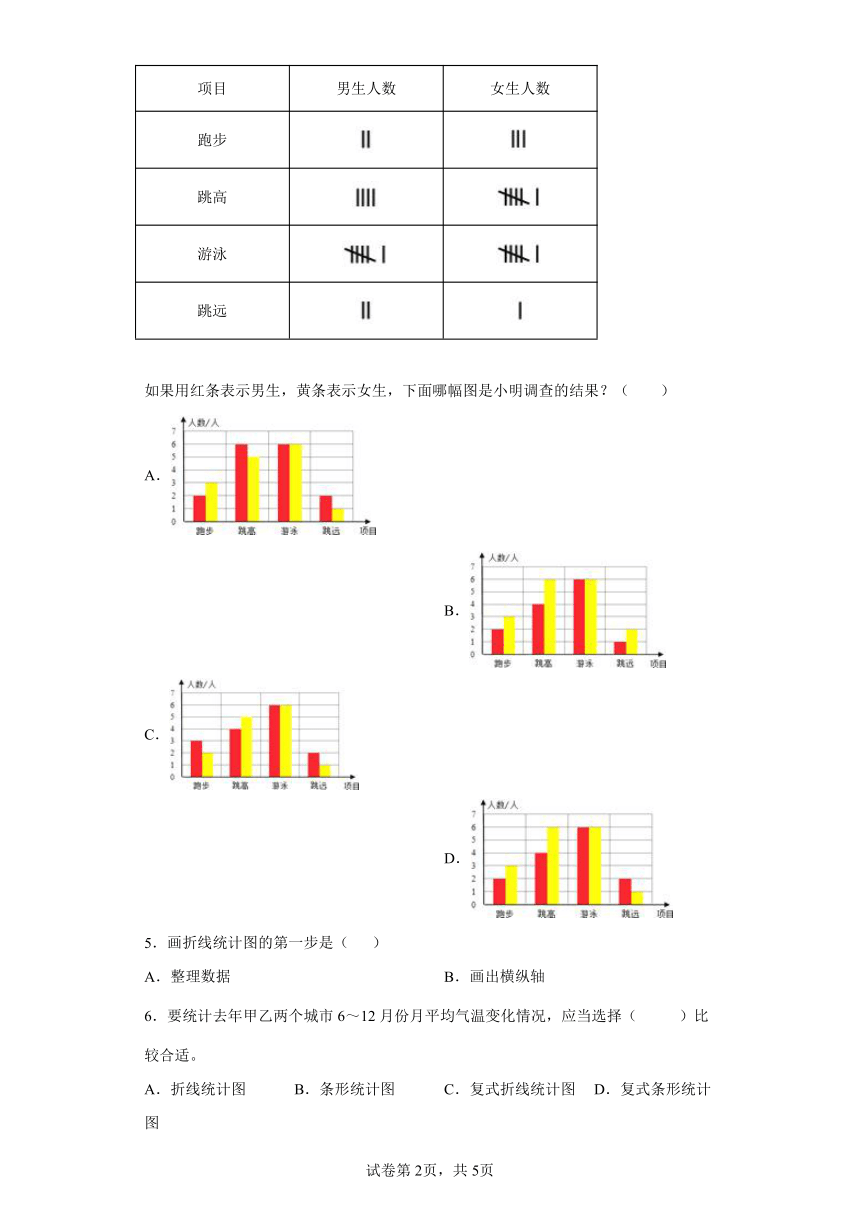
4.小明调查了一些同学最喜欢的运动项目是什么,把他收集的数据记录在下面的表内:
项目 男生人数 女生人数
跑步
跳高
游泳
跳远
如果用红条表示男生,黄条表示女生,下面哪幅图是小明调查的结果?( )A. B.
C. D.
5.画折线统计图的第一步是( )
A.整理数据 B.画出横纵轴
6.要统计去年甲乙两个城市6~12月份月平均气温变化情况,应当选择( )比较合适。
A.折线统计图 B.条形统计图 C.复式折线统计图 D.复式条形统计图
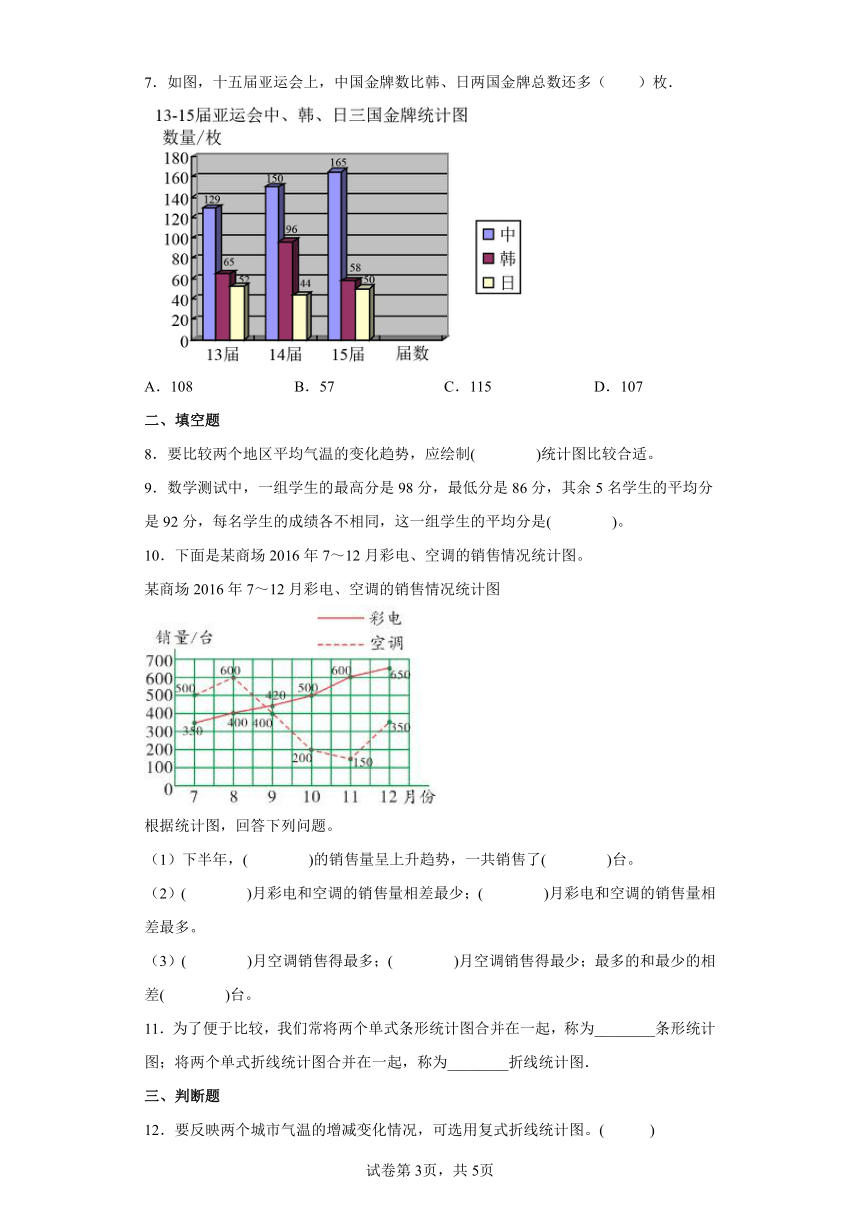
7.如图,十五届亚运会上,中国金牌数比韩、日两国金牌总数还多( )枚.
A.108 B.57 C.115 D.107
二、填空题
8.要比较两个地区平均气温的变化趋势,应绘制( )统计图比较合适。
9.数学测试中,一组学生的最高分是98分,最低分是86分,其余5名学生的平均分是92分,每名学生的成绩各不相同,这一组学生的平均分是( )。
10.下面是某商场2016年7~12月彩电、空调的销售情况统计图。
某商场2016年7~12月彩电、空调的销售情况统计图
根据统计图,回答下列问题。
(1)下半年,( )的销售量呈上升趋势,一共销售了( )台。
(2)( )月彩电和空调的销售量相差最少;( )月彩电和空调的销售量相差最多。
(3)( )月空调销售得最多;( )月空调销售得最少;最多的和最少的相差( )台。
11.为了便于比较,我们常将两个单式条形统计图合并在一起,称为________条形统计图;将两个单式折线统计图合并在一起,称为________折线统计图.
三、判断题
12.要反映两个城市气温的增减变化情况,可选用复式折线统计图。( )
13.五个数的平均数一定小于最大的两个数,大于最小的两个数。( )
14.陈强语文、英语、数学三科的平均成绩是92分,其中语文91分,英语88分,由此判定数学成绩一定高于92分。( )
15.比较两个城市的月平均气温变化情况,用复式条形统计图更合适。( )
四、解答题
16.下面是光明小学2012年入学的学生从一年级到六年级这6年的近视人数统计表.
年级 一年级 二年级 三年级 四年级 五年级 六年级
近视人数 4 12 28 40 56 60
(1)根据统计表完成折线统计图.
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是( ).
(3)从( )年级到( )年级近视人数上升得最慢.
17.下面是甲、乙两名射击队员连续射击成绩的统计图。
(1)甲、乙两人六次射击的平均成绩分别是多少?
(2)如果要从两人中选一人参加比赛,你觉得选谁合适?写出你的想法。
18.小芳五天看完一本数学故事书,下面是她看书的情况。
时间 第一天 第二天 第三天 第四天 第五天
页数 34 40 46 42 38
(1)前两天,小芳平均每天看书多少页?
(2)这五天小芳平均每天看书多少页?
(3)哪几天看书页数比平均每天看的页数少?
19.甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克.求四人的平均体重是多少千克?
20.斌斌商场的经理为了了解两个不同产地的同一种水果的销售情况,收集了10个省会城市的销售批发价格,如下表:(单位:元/千克)
产地 长沙 武汉 广州 海口 福州 昆明 南宁 南昌 南京 郑州
甲 0.85 0.83 0.90 0.90 0.88 0.86 0.82 0.81 0.95 0.84
乙 0.80 0.82 0.95 0.91 0.86 0.82 0.83 0.79 0.84 0.80
(1)哪种水果的平均批发价较高?
(2)如果你是该商场经理,你将作出怎样的经营决策?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
略
2.D
【解析】
【详解】
略
3.B
【解析】
平均数与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低。
【详解】
根据分析可知,如果想尽可能减小误差,得到这个圆的周长,就要把极端值(14.8)去掉,把剩余的7个数据加起来除以7。
故答案为:B
【点睛】
通常把影响平均数的极端值去掉,再根据平均数的求法求出平均数,结果较为准确。
4.D
【解析】
【详解】
根据统计表可知,跑步的男生有2人、女生有3人,跳高的男生有4人、女生有6人,游泳的男生有6人、女生有6人,跳远的男生有2人、女生有1人,根据这些数据选择条形统计图即可得到答案.
5.A
【解析】
【详解】
略
6.C
【解析】
【分析】
根据题意分析可知,条形统计图能反映出数据的多少,折线统计图不仅能反映出数据的多少也能反映出数据的增减变化情况。据此解答。
【详解】
复式折线统计图不但可以表示两个不同数值的多少,而且能够清楚地表示出数量增减变化的情况和两者之间的对比情况,所以要统计两个城市1~6月份月平均气温变化情况,用复式折线统计图比较合适。
故答案是:C
【点睛】
掌握不同统计图的特点是解答本题的关键。
7.B
【解析】
【详解】
165﹣(58+50)
=165﹣108
=57(枚)
答:中国金牌数比韩、日两国金牌总数还多57枚.
8.复式折线
【解析】
【分析】
条形统计图的特征:能够清楚的看出数量的多少;折线统计图的特征:能够清楚的反应出数量的增减变化情况;如果是两组或两组以上的数据,则采用复式统计图,由此即可解答。
【详解】
由分析可知,两个地区平均气温的变化趋势,应绘制复式折线统计图比较合适。
【点睛】
本题主要考查统计图的特征,熟练掌握统计图的特征并灵活运用。
9.92分
【解析】
【分析】
平均分=学生的总份数÷学生人数,据此解答。
【详解】
(98+86+92×5)÷(5+2)
=644÷7
=92(分)
这一组学生的平均分是92分。
【点睛】
此题考查了平均数的求法,明确平均数=总数量÷份数。
10. 彩电 2920 9 11 8 11 450
【解析】
略
11. 复式 复式
【解析】
【详解】
单式条形统计图或单式折线统计图只能表示一种数据;复式条形统计图或复式折线统计图能表示两种或两种以上的数据.
12.√
【解析】
【分析】
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,据此解答。
【详解】
要反映两个城市气温的增减变化情况,可选用复式折线统计图。
故答案为:√
【点睛】
掌握折线统计图的特点是解答此题的关键。
13.×
【解析】
【分析】
根据平均数据的意义,一组数据的平均数就是各数之和除以这组数据的个数,因此,平均数是在最大数和最小数之间;题目中五个数的平均数一定小于最大的两个数,大于最小的两个数不一定正确,举一反例即可判断。
【详解】
由平均数的意义及求法可知,平均数应该在最大数和最小数之间,但不一定小于最大的两个数或大于最小的两个数。
例:50、4、3、2、1这组数中最大的两个数是50和4,这组数的平均数为:
(50+4+3+2+1)÷5
=60÷5
=12
12<60,12>4,所以,五个数的平均数一定小于最大的两个数,大于最小的两个数的说法错误。
故答案为:×
【点睛】
此题考查了平均数的意义,一组数据的平均数一定大于这组数据中最小的数,小于最大的数,即在最大数和最小数之间。
14.√
【解析】
【分析】
根据语文、数学、英语三科的平均成绩是92分,由此可以求出三科的总成绩,然后用总成绩减去语文和英语的成绩即可求出数学的成绩,再与92分比较即可判断。
【详解】
92×3﹣91﹣88
=276﹣91﹣88
=185﹣88
=97(分)
97>92
数学成绩一定高于92分,原题说法正确。
故答案为:√。
15.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化;据此解答。
【详解】
根据题意可知,是两个城市,比较两个城市的月平均气温变化情况,用复式折线统计图更合适。
原题干比较两个城市的月平均气温变化情况,用复式条形统计图更合适,是错误的。
故答案为:×
【点睛】
本题考查统计图的选择,根据统计图的各自特点,进行解答。
16.(1)如图:
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是上升.
(3)从五年级到六年级近视人数上升得最慢.
【解析】
【详解】
(1)横轴表示年级,竖轴表示人数,一格表示4人,根据统计表中的数据先找出对应的点,然后把这些点顺次连接绘制成折线统计图;
(2)根据折线的走势判断近视人数的趋势;
(3)根据折线上升的程度结合数据判断上升最慢的阶段即可.
17.(1)甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【解析】
【分析】
(1)通过折线统计图收集数据:甲6次射击的分数为: 8,9,10,9,8,10;乙6次射击的成绩为: 9,8,8, 9,10,10;然后用各自分数的和:射击的次数得到平均数即可。
{2)通过统计图发现,甲的成绩波动较大,而乙的发挥呈上升趋势。
【详解】
(1)甲:(8+9+10+9+8+10)÷6
=54÷6
=9(环)
乙:(9+8+8+9+10+10)÷6
=54÷6
=9(环)
答:甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【点睛】
本题考查了从复式折线统计图获取信的能力。折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况。
18.(1)(34+40)÷2=37(页)
(2)(34+40+46+42+38)÷5=40(页)
(3)第一天和第五天。
【解析】
略
19.41.5千克
【解析】
【详解】
120-2×40=40(千克)
126-2×40=46(千克)
(40+46+2×40)÷4=41.5(千克)
答:四人的平均体重是41.5千克.
20.(1)产地甲的水果平均批发价较高;
(2)多进乙地的水果。
【解析】
略
答案第1页,共2页
答案第1页,共2页
一、选择题
1.单式折线统计图和复式折线统计图的区别是( )
A.单式折线统计图表示出数量的多少,复式折线统计图能反映出数据的变化情况.
B.单式折线统计图比较简单,复式折线统计图不容易看懂.
C.单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示出两组或两组以上的数据的增减变化情况.
2.一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游去,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图像,若不计转向时间,则从开始起到3分钟止他们相遇的次数为( )
A.2次 B.3次 C.4次 D.5次
3.8名同学用软尺测量同一个圆的周长,测量结果如下表:
学号 1 2 3 4 5 6 7 8
周长/cm 9.1 8.9 9.0 9.2 9.1 14.8 9.1 9.03
如果想尽可能减小误差,得到这个圆的周长,你会建议他们选择( )方法。A.采用出现次数最多的9.1 B.去掉14.8把剩余的7个数据加起来除以7
C.把8个数据加起来除以8 D.选择小数点后有两位小数的9.03
4.小明调查了一些同学最喜欢的运动项目是什么,把他收集的数据记录在下面的表内:
项目 男生人数 女生人数
跑步
跳高
游泳
跳远
如果用红条表示男生,黄条表示女生,下面哪幅图是小明调查的结果?( )A. B.
C. D.
5.画折线统计图的第一步是( )
A.整理数据 B.画出横纵轴
6.要统计去年甲乙两个城市6~12月份月平均气温变化情况,应当选择( )比较合适。
A.折线统计图 B.条形统计图 C.复式折线统计图 D.复式条形统计图
7.如图,十五届亚运会上,中国金牌数比韩、日两国金牌总数还多( )枚.
A.108 B.57 C.115 D.107
二、填空题
8.要比较两个地区平均气温的变化趋势,应绘制( )统计图比较合适。
9.数学测试中,一组学生的最高分是98分,最低分是86分,其余5名学生的平均分是92分,每名学生的成绩各不相同,这一组学生的平均分是( )。
10.下面是某商场2016年7~12月彩电、空调的销售情况统计图。
某商场2016年7~12月彩电、空调的销售情况统计图
根据统计图,回答下列问题。
(1)下半年,( )的销售量呈上升趋势,一共销售了( )台。
(2)( )月彩电和空调的销售量相差最少;( )月彩电和空调的销售量相差最多。
(3)( )月空调销售得最多;( )月空调销售得最少;最多的和最少的相差( )台。
11.为了便于比较,我们常将两个单式条形统计图合并在一起,称为________条形统计图;将两个单式折线统计图合并在一起,称为________折线统计图.
三、判断题
12.要反映两个城市气温的增减变化情况,可选用复式折线统计图。( )
13.五个数的平均数一定小于最大的两个数,大于最小的两个数。( )
14.陈强语文、英语、数学三科的平均成绩是92分,其中语文91分,英语88分,由此判定数学成绩一定高于92分。( )
15.比较两个城市的月平均气温变化情况,用复式条形统计图更合适。( )
四、解答题
16.下面是光明小学2012年入学的学生从一年级到六年级这6年的近视人数统计表.
年级 一年级 二年级 三年级 四年级 五年级 六年级
近视人数 4 12 28 40 56 60
(1)根据统计表完成折线统计图.
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是( ).
(3)从( )年级到( )年级近视人数上升得最慢.
17.下面是甲、乙两名射击队员连续射击成绩的统计图。
(1)甲、乙两人六次射击的平均成绩分别是多少?
(2)如果要从两人中选一人参加比赛,你觉得选谁合适?写出你的想法。
18.小芳五天看完一本数学故事书,下面是她看书的情况。
时间 第一天 第二天 第三天 第四天 第五天
页数 34 40 46 42 38
(1)前两天,小芳平均每天看书多少页?
(2)这五天小芳平均每天看书多少页?
(3)哪几天看书页数比平均每天看的页数少?
19.甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克.求四人的平均体重是多少千克?
20.斌斌商场的经理为了了解两个不同产地的同一种水果的销售情况,收集了10个省会城市的销售批发价格,如下表:(单位:元/千克)
产地 长沙 武汉 广州 海口 福州 昆明 南宁 南昌 南京 郑州
甲 0.85 0.83 0.90 0.90 0.88 0.86 0.82 0.81 0.95 0.84
乙 0.80 0.82 0.95 0.91 0.86 0.82 0.83 0.79 0.84 0.80
(1)哪种水果的平均批发价较高?
(2)如果你是该商场经理,你将作出怎样的经营决策?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
略
2.D
【解析】
【详解】
略
3.B
【解析】
平均数与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低。
【详解】
根据分析可知,如果想尽可能减小误差,得到这个圆的周长,就要把极端值(14.8)去掉,把剩余的7个数据加起来除以7。
故答案为:B
【点睛】
通常把影响平均数的极端值去掉,再根据平均数的求法求出平均数,结果较为准确。
4.D
【解析】
【详解】
根据统计表可知,跑步的男生有2人、女生有3人,跳高的男生有4人、女生有6人,游泳的男生有6人、女生有6人,跳远的男生有2人、女生有1人,根据这些数据选择条形统计图即可得到答案.
5.A
【解析】
【详解】
略
6.C
【解析】
【分析】
根据题意分析可知,条形统计图能反映出数据的多少,折线统计图不仅能反映出数据的多少也能反映出数据的增减变化情况。据此解答。
【详解】
复式折线统计图不但可以表示两个不同数值的多少,而且能够清楚地表示出数量增减变化的情况和两者之间的对比情况,所以要统计两个城市1~6月份月平均气温变化情况,用复式折线统计图比较合适。
故答案是:C
【点睛】
掌握不同统计图的特点是解答本题的关键。
7.B
【解析】
【详解】
165﹣(58+50)
=165﹣108
=57(枚)
答:中国金牌数比韩、日两国金牌总数还多57枚.
8.复式折线
【解析】
【分析】
条形统计图的特征:能够清楚的看出数量的多少;折线统计图的特征:能够清楚的反应出数量的增减变化情况;如果是两组或两组以上的数据,则采用复式统计图,由此即可解答。
【详解】
由分析可知,两个地区平均气温的变化趋势,应绘制复式折线统计图比较合适。
【点睛】
本题主要考查统计图的特征,熟练掌握统计图的特征并灵活运用。
9.92分
【解析】
【分析】
平均分=学生的总份数÷学生人数,据此解答。
【详解】
(98+86+92×5)÷(5+2)
=644÷7
=92(分)
这一组学生的平均分是92分。
【点睛】
此题考查了平均数的求法,明确平均数=总数量÷份数。
10. 彩电 2920 9 11 8 11 450
【解析】
略
11. 复式 复式
【解析】
【详解】
单式条形统计图或单式折线统计图只能表示一种数据;复式条形统计图或复式折线统计图能表示两种或两种以上的数据.
12.√
【解析】
【分析】
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,据此解答。
【详解】
要反映两个城市气温的增减变化情况,可选用复式折线统计图。
故答案为:√
【点睛】
掌握折线统计图的特点是解答此题的关键。
13.×
【解析】
【分析】
根据平均数据的意义,一组数据的平均数就是各数之和除以这组数据的个数,因此,平均数是在最大数和最小数之间;题目中五个数的平均数一定小于最大的两个数,大于最小的两个数不一定正确,举一反例即可判断。
【详解】
由平均数的意义及求法可知,平均数应该在最大数和最小数之间,但不一定小于最大的两个数或大于最小的两个数。
例:50、4、3、2、1这组数中最大的两个数是50和4,这组数的平均数为:
(50+4+3+2+1)÷5
=60÷5
=12
12<60,12>4,所以,五个数的平均数一定小于最大的两个数,大于最小的两个数的说法错误。
故答案为:×
【点睛】
此题考查了平均数的意义,一组数据的平均数一定大于这组数据中最小的数,小于最大的数,即在最大数和最小数之间。
14.√
【解析】
【分析】
根据语文、数学、英语三科的平均成绩是92分,由此可以求出三科的总成绩,然后用总成绩减去语文和英语的成绩即可求出数学的成绩,再与92分比较即可判断。
【详解】
92×3﹣91﹣88
=276﹣91﹣88
=185﹣88
=97(分)
97>92
数学成绩一定高于92分,原题说法正确。
故答案为:√。
15.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化;据此解答。
【详解】
根据题意可知,是两个城市,比较两个城市的月平均气温变化情况,用复式折线统计图更合适。
原题干比较两个城市的月平均气温变化情况,用复式条形统计图更合适,是错误的。
故答案为:×
【点睛】
本题考查统计图的选择,根据统计图的各自特点,进行解答。
16.(1)如图:
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是上升.
(3)从五年级到六年级近视人数上升得最慢.
【解析】
【详解】
(1)横轴表示年级,竖轴表示人数,一格表示4人,根据统计表中的数据先找出对应的点,然后把这些点顺次连接绘制成折线统计图;
(2)根据折线的走势判断近视人数的趋势;
(3)根据折线上升的程度结合数据判断上升最慢的阶段即可.
17.(1)甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【解析】
【分析】
(1)通过折线统计图收集数据:甲6次射击的分数为: 8,9,10,9,8,10;乙6次射击的成绩为: 9,8,8, 9,10,10;然后用各自分数的和:射击的次数得到平均数即可。
{2)通过统计图发现,甲的成绩波动较大,而乙的发挥呈上升趋势。
【详解】
(1)甲:(8+9+10+9+8+10)÷6
=54÷6
=9(环)
乙:(9+8+8+9+10+10)÷6
=54÷6
=9(环)
答:甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【点睛】
本题考查了从复式折线统计图获取信的能力。折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况。
18.(1)(34+40)÷2=37(页)
(2)(34+40+46+42+38)÷5=40(页)
(3)第一天和第五天。
【解析】
略
19.41.5千克
【解析】
【详解】
120-2×40=40(千克)
126-2×40=46(千克)
(40+46+2×40)÷4=41.5(千克)
答:四人的平均体重是41.5千克.
20.(1)产地甲的水果平均批发价较高;
(2)多进乙地的水果。
【解析】
略
答案第1页,共2页
答案第1页,共2页
