17.2 勾股定理的逆定理的应用 第2课时 课件(共21张PPT)
文档属性
| 名称 | 17.2 勾股定理的逆定理的应用 第2课时 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 17:28:33 | ||
图片预览







文档简介
(共21张PPT)
2022年春人教版数学
八年级下册数学精品课件
17.2 勾股定理的逆定理
第2课时 勾股定理的逆定理应用
第十七章 勾股定理
情境引入
1.灵活应用勾股定理及其逆定理解决实际问题.(重点)
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点)
学习目标
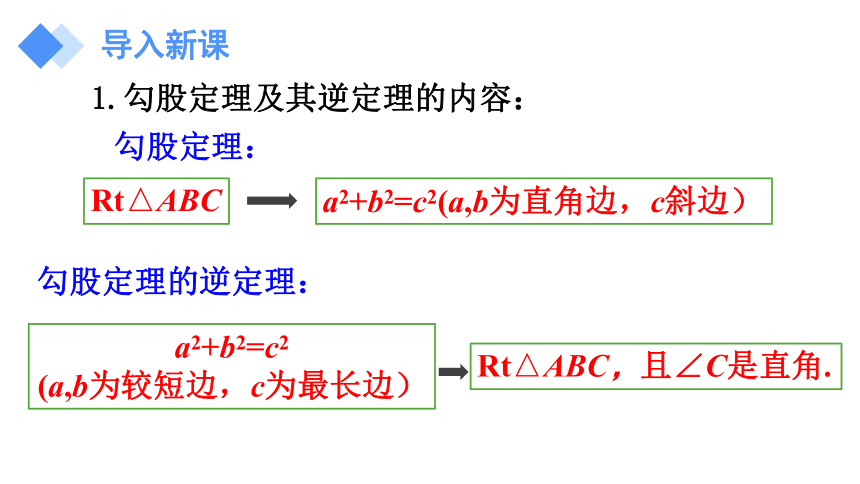
1.勾股定理及其逆定理的内容:
a2+b2=c2(a,b为直角边,c斜边)
Rt△ABC
勾股定理:
勾股定理的逆定理:
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
导入新课
2.等腰△ ABC中,AB=AC=10cm,BC=12cm,则BC边上的高是 cm.
8
3.已知△ ABC中,BC=41,AC=40,AB=9,则此三角形为 三角形, 是最大角.
直角
∠A
如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,
“远航”号每小时航行16海里,“海天”号每小时航行12海
里.它们离开港口一个半小时后分别位于Q、R处,且相距30
海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗
N
E
P
Q
R
1
2
勾股定理的逆定理的应用
讲授新课
例1
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302,即PQ2+PR2=QR2,所以∠QPR=90°.
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=450,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
勾股定理及其逆定理在解决航海问题时,理解方位角的含义是前提,画出符合题意的图形,标明已知条件,转化为解决直角三角形问题所需的条件.
归纳
勾股定理及其逆定理的综合应用
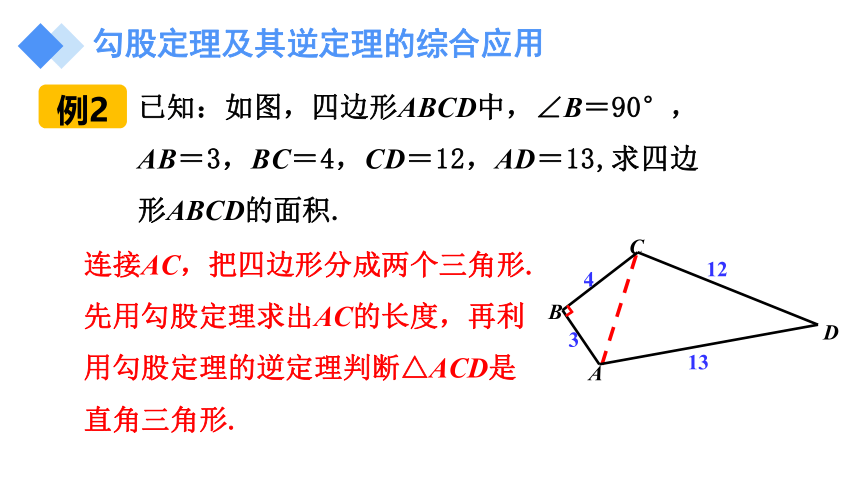
已知:如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
例2
A
D
B
C
3
4
13
12
解:连接AC.
四边形问题对角线是常用的辅助线,它把四边形问题转化成两个三角形的问题.在使用勾股定理的逆定理解决问题时,它与勾股定理是”黄金搭挡”,经常配套使用.
归纳
如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积.
A
B
C
3
4
13
12
D
解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,∴AC2+BC2=AB2,∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=24(m2).
变式训练
1.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
C
a
b
c
l
第1题
当堂练习
2. 如图,△ABC的顶点A,B,C,在边长为1的正方形方格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
A
B
C
D
第2题
C
3. 医院、公园和超市的平面示意图如图所示,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的北偏东 的方向.
东
医院
公园
超市
北
65°
4.如图,等边三角形的边长为6,则高AD的长是 ;这个三角形的面积是 .
A
B
C
D
5. 如图,矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠,点D落在E处,则重叠部分△AFC的面积是多少
解:
解得AF=
△AFC的面积是
因为将矩形沿AC折叠,点D落在E处,所以AE=AD=6,∠B=90°,
又因为AD=BC,CD=AB=8,
∠AFE=∠ CFB,所以△AFC≌△CFB,所以BF=8-AF=EF.
在Rt△AEF中,AF =AE +EF ,即AF =6 +(8-AF) ,
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题.
四边形问题
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
17.2 勾股定理的逆定理
第2课时 勾股定理的逆定理应用
第十七章 勾股定理
情境引入
1.灵活应用勾股定理及其逆定理解决实际问题.(重点)
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点)
学习目标
1.勾股定理及其逆定理的内容:
a2+b2=c2(a,b为直角边,c斜边)
Rt△ABC
勾股定理:
勾股定理的逆定理:
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
导入新课
2.等腰△ ABC中,AB=AC=10cm,BC=12cm,则BC边上的高是 cm.
8
3.已知△ ABC中,BC=41,AC=40,AB=9,则此三角形为 三角形, 是最大角.
直角
∠A
如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,
“远航”号每小时航行16海里,“海天”号每小时航行12海
里.它们离开港口一个半小时后分别位于Q、R处,且相距30
海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗
N
E
P
Q
R
1
2
勾股定理的逆定理的应用
讲授新课
例1
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302,即PQ2+PR2=QR2,所以∠QPR=90°.
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=450,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
勾股定理及其逆定理在解决航海问题时,理解方位角的含义是前提,画出符合题意的图形,标明已知条件,转化为解决直角三角形问题所需的条件.
归纳
勾股定理及其逆定理的综合应用
已知:如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
例2
A
D
B
C
3
4
13
12
解:连接AC.
四边形问题对角线是常用的辅助线,它把四边形问题转化成两个三角形的问题.在使用勾股定理的逆定理解决问题时,它与勾股定理是”黄金搭挡”,经常配套使用.
归纳
如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积.
A
B
C
3
4
13
12
D
解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,∴AC2+BC2=AB2,∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=24(m2).
变式训练
1.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
C
a
b
c
l
第1题
当堂练习
2. 如图,△ABC的顶点A,B,C,在边长为1的正方形方格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
A
B
C
D
第2题
C
3. 医院、公园和超市的平面示意图如图所示,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的北偏东 的方向.
东
医院
公园
超市
北
65°
4.如图,等边三角形的边长为6,则高AD的长是 ;这个三角形的面积是 .
A
B
C
D
5. 如图,矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠,点D落在E处,则重叠部分△AFC的面积是多少
解:
解得AF=
△AFC的面积是
因为将矩形沿AC折叠,点D落在E处,所以AE=AD=6,∠B=90°,
又因为AD=BC,CD=AB=8,
∠AFE=∠ CFB,所以△AFC≌△CFB,所以BF=8-AF=EF.
在Rt△AEF中,AF =AE +EF ,即AF =6 +(8-AF) ,
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题.
四边形问题
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
