18.1.1 平行四边形的边、角的特征 第1课时 课件(共24张PPT)
文档属性
| 名称 | 18.1.1 平行四边形的边、角的特征 第1课时 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 17:22:18 | ||
图片预览





文档简介
(共24张PPT)
2022年春人教版数学
八年级下册数学精品课件
18.1.1平行四边形的性质
第1课时 平行四边形的边、角特征
第十八章 平行四边形
情境引入
1.理解并掌握平行四边形的概念及其性质.(重点)
2.根据平行四边形的性质进行简单的计算和证明.(难点)
学习目标
导入新课
图片欣赏
A
B
C
A
B
C
D
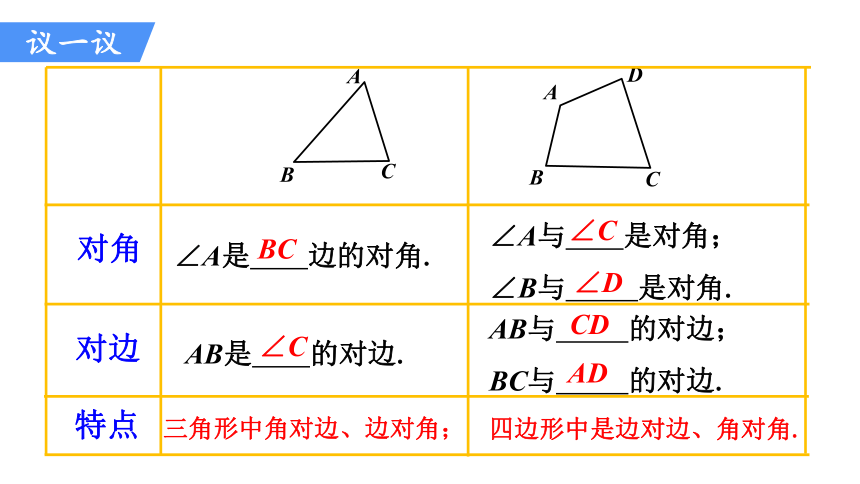
对角
对边
∠A是 边的对角.
∠A与 是对角;
∠B与 是对角.
AB是 的对边.
AB与 的对边;
BC与 的对边.
三角形中角对边、边对角;
特点
BC
CD
AD
∠C
∠D
∠C
四边形中是边对边、角对角.
议一议
平行四边形的定义
用两个全等的三角形,能拼出怎样的四边形? 拼拼看.
讲授新课
问题1
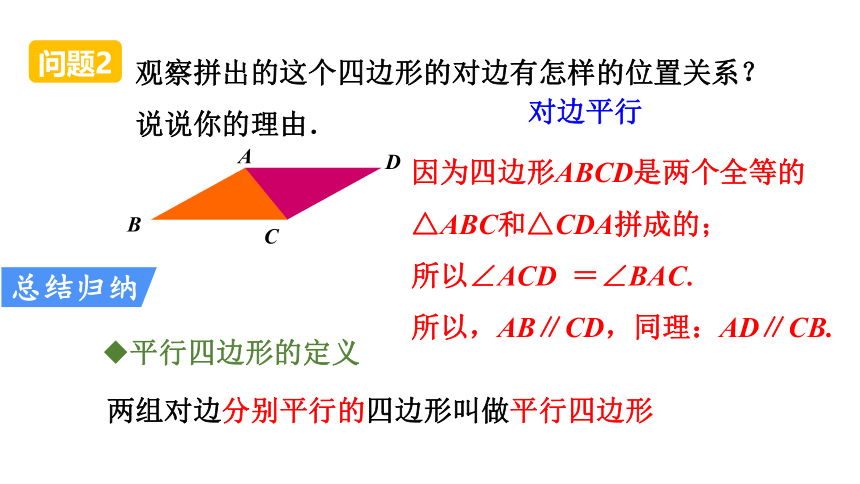
观察拼出的这个四边形的对边有怎样的位置关系?说说你的理由.
对边平行
A
B
C
D
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形
总结归纳
问题2
因为四边形ABCD是两个全等的△ABC和△CDA拼成的;
所以∠ACD =∠BAC.
所以,AB∥CD,同理:AD∥CB.
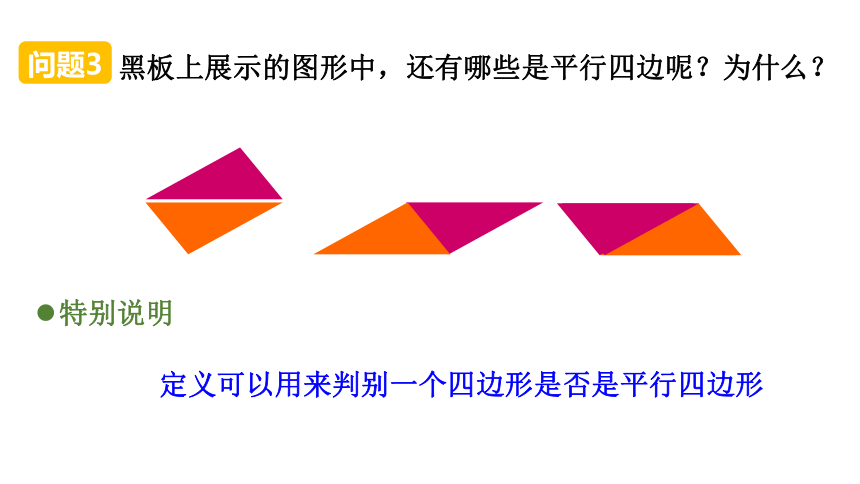
黑板上展示的图形中,还有哪些是平行四边呢?为什么?
定义可以用来判别一个四边形是否是平行四边形
特别说明
问题3
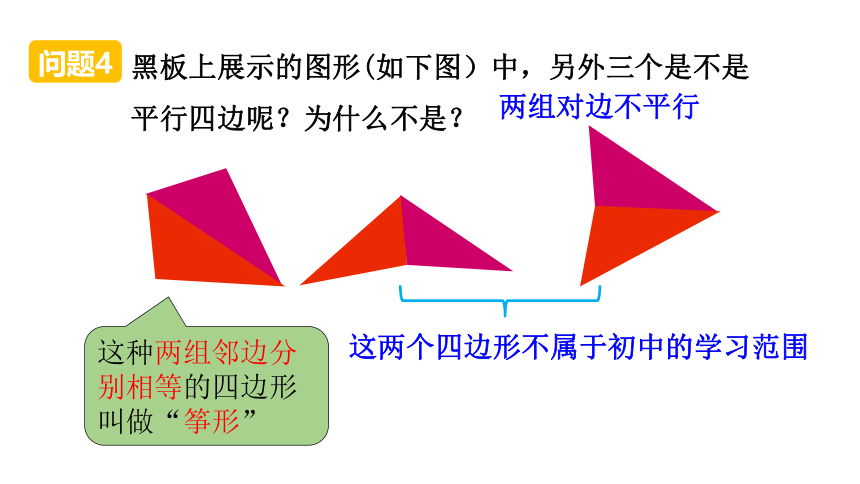
黑板上展示的图形(如下图)中,另外三个是不是平行四边呢?为什么不是?
两组对边不平行
这两个四边形不属于初中的学习范围
这种两组邻边分别相等的四边形叫做“筝形”
问题4
只有一组对边平行的四边形是不是平行四边形呢?是什么特殊四边形?
不是平行四边形,是梯形.
问题5
D
A
B
C
记作: ABCD
读作: 平行四边形ABCD
平行四边形的相关概念
记法与读法
相关元素
对角:∠A与∠C, ∠B与∠D.
对边:AB 与CD, AD与BC.
对角线:AC、BD.
平行四边形的性质
研究等腰三角形的性质是从哪些方面考虑的?
边和角
边和角
1.小组合作:同学们利用学具(全等的三角形纸板).
探究方法
2.汇报结论:学生展示实验过程,相互补充探究出的结论.
3.说理验证:请大家思考一下,利用我们以前学习的几何知识通过说理能验证这三个结论吗?
那么研究平行四边形首先可以从哪些方面考虑?
问题6
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
1.同学们自己证明∠BAD=∠DCB
2.不添加辅助线,你能否
直接运用平行四边形的定义,
证明其对角相等?
A
B
C
D
说理验证
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
A
B
C
D
总结归纳
如图,在□ABCD中
(1)若∠A=130°,则∠B=_____ ,∠C=_____ , ∠D=_____。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
例1
典例精析
D
A
B
C
F
E
证明:
平行四边形为证明线段及角相等提供了一种新的思路.
归纳
例2
如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
∵四边形ABCD是平行四边形,
∴∠ A=∠ C, AD=CB ,
又∠ AED = ∠ CFB = 90°,
∴ △ADE≌ △CBF.
∴AE=CF.
两条平行线间的距离
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离相等
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(因为平行四边形的对边相等)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
当堂练习
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55°
C. 65° D. 75°
A
A
B
C
M
D
2.在□ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A .3 B. 5 C. 2或3 D. 3或5
D
3.在□ABCD中, ∠A: ∠B: ∠C=1:2:1,则∠D等于 .
120°
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
5.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
18.1.1平行四边形的性质
第1课时 平行四边形的边、角特征
第十八章 平行四边形
情境引入
1.理解并掌握平行四边形的概念及其性质.(重点)
2.根据平行四边形的性质进行简单的计算和证明.(难点)
学习目标
导入新课
图片欣赏
A
B
C
A
B
C
D
对角
对边
∠A是 边的对角.
∠A与 是对角;
∠B与 是对角.
AB是 的对边.
AB与 的对边;
BC与 的对边.
三角形中角对边、边对角;
特点
BC
CD
AD
∠C
∠D
∠C
四边形中是边对边、角对角.
议一议
平行四边形的定义
用两个全等的三角形,能拼出怎样的四边形? 拼拼看.
讲授新课
问题1
观察拼出的这个四边形的对边有怎样的位置关系?说说你的理由.
对边平行
A
B
C
D
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形
总结归纳
问题2
因为四边形ABCD是两个全等的△ABC和△CDA拼成的;
所以∠ACD =∠BAC.
所以,AB∥CD,同理:AD∥CB.
黑板上展示的图形中,还有哪些是平行四边呢?为什么?
定义可以用来判别一个四边形是否是平行四边形
特别说明
问题3
黑板上展示的图形(如下图)中,另外三个是不是平行四边呢?为什么不是?
两组对边不平行
这两个四边形不属于初中的学习范围
这种两组邻边分别相等的四边形叫做“筝形”
问题4
只有一组对边平行的四边形是不是平行四边形呢?是什么特殊四边形?
不是平行四边形,是梯形.
问题5
D
A
B
C
记作: ABCD
读作: 平行四边形ABCD
平行四边形的相关概念
记法与读法
相关元素
对角:∠A与∠C, ∠B与∠D.
对边:AB 与CD, AD与BC.
对角线:AC、BD.
平行四边形的性质
研究等腰三角形的性质是从哪些方面考虑的?
边和角
边和角
1.小组合作:同学们利用学具(全等的三角形纸板).
探究方法
2.汇报结论:学生展示实验过程,相互补充探究出的结论.
3.说理验证:请大家思考一下,利用我们以前学习的几何知识通过说理能验证这三个结论吗?
那么研究平行四边形首先可以从哪些方面考虑?
问题6
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
1.同学们自己证明∠BAD=∠DCB
2.不添加辅助线,你能否
直接运用平行四边形的定义,
证明其对角相等?
A
B
C
D
说理验证
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
A
B
C
D
总结归纳
如图,在□ABCD中
(1)若∠A=130°,则∠B=_____ ,∠C=_____ , ∠D=_____。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
例1
典例精析
D
A
B
C
F
E
证明:
平行四边形为证明线段及角相等提供了一种新的思路.
归纳
例2
如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
∵四边形ABCD是平行四边形,
∴∠ A=∠ C, AD=CB ,
又∠ AED = ∠ CFB = 90°,
∴ △ADE≌ △CBF.
∴AE=CF.
两条平行线间的距离
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离相等
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(因为平行四边形的对边相等)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
当堂练习
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55°
C. 65° D. 75°
A
A
B
C
M
D
2.在□ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A .3 B. 5 C. 2或3 D. 3或5
D
3.在□ABCD中, ∠A: ∠B: ∠C=1:2:1,则∠D等于 .
120°
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
5.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
