2021-2022学年人教版数学八年级下册18.2.1 矩形 课件(2课时、共23张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.2.1 矩形 课件(2课时、共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 15:26:18 | ||
图片预览


文档简介
(共23张PPT)
18.2.1 矩形
(第1课时)
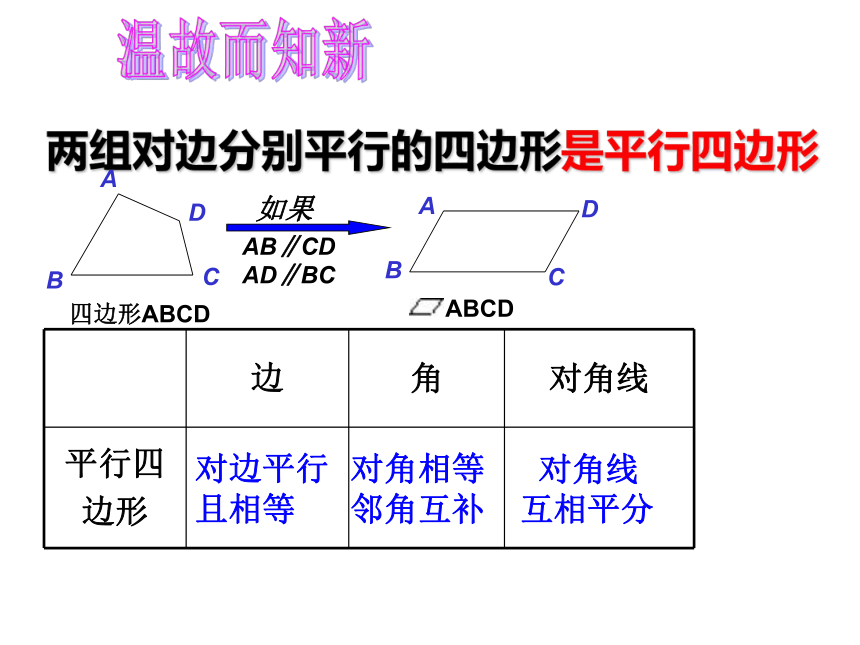
温故而知新
边 角 对角线
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
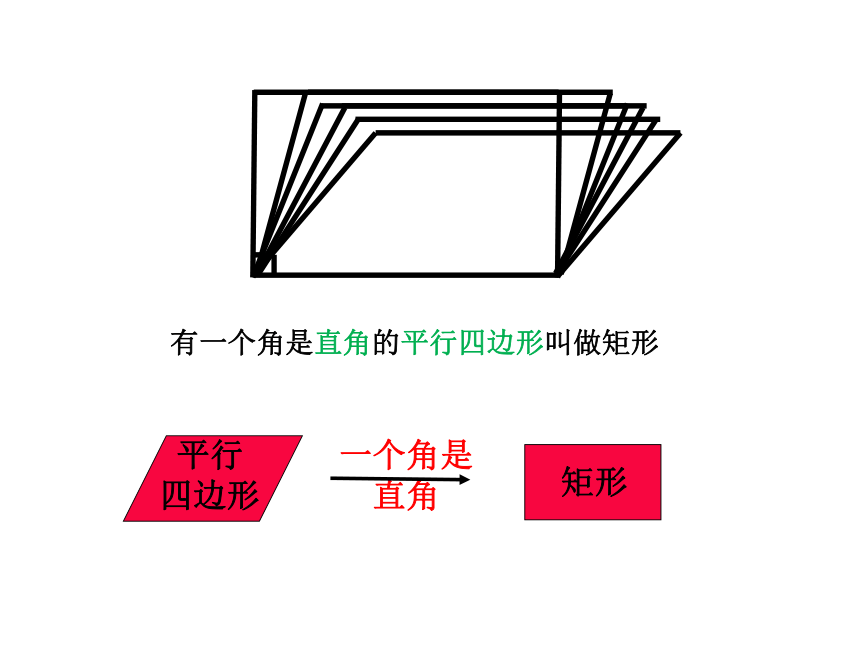
一个角是
直角
平行
四边形
矩形
有一个角是直角的平行四边形叫做矩形
生活中的实例
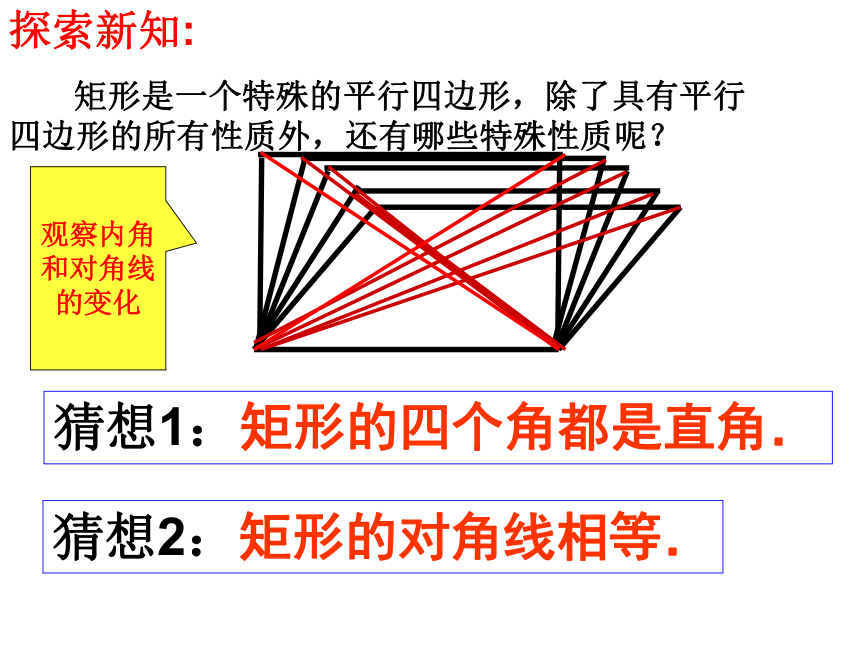
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
观察内角和对角线的变化
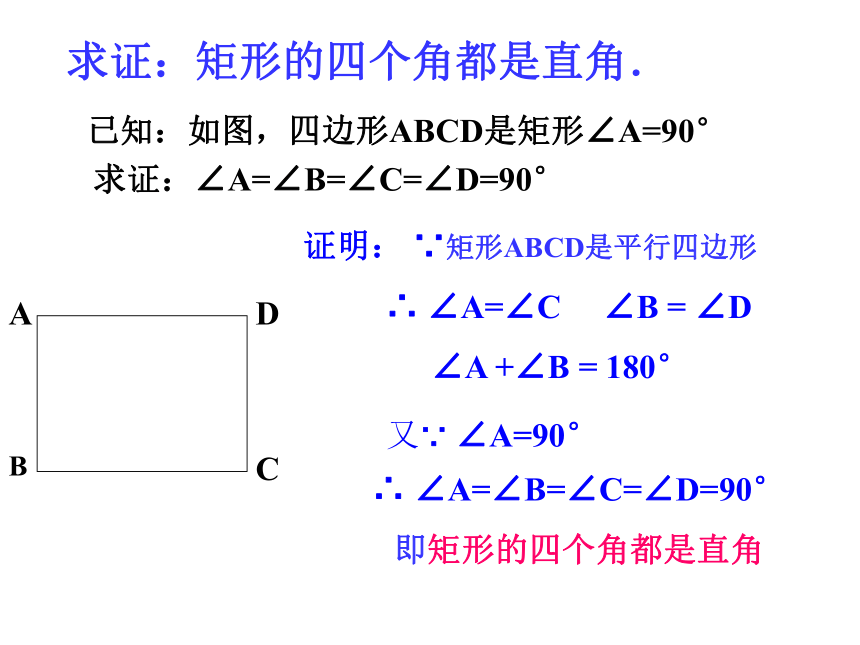
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形∠A=90°
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵矩形ABCD是平行四边形
又∵ ∠A=90°
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
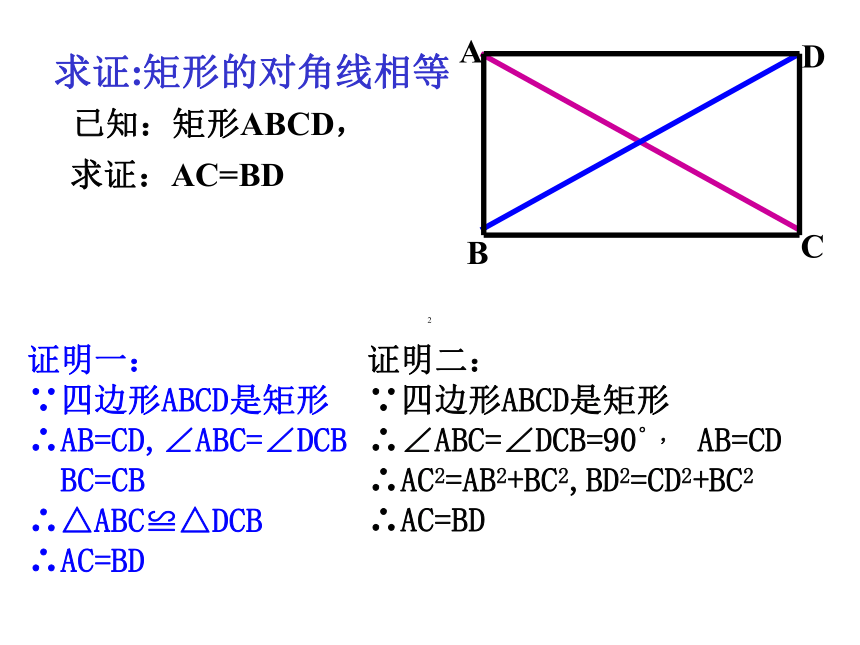
求证:矩形的对角线相等
A
D
C
B
已知:矩形ABCD,
求证:AC=BD
证明一:
∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB
∴AC=BD
证明二:
∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°, AB=CD
∴AC2=AB2+BC2,BD2=CD2+BC2
∴AC=BD
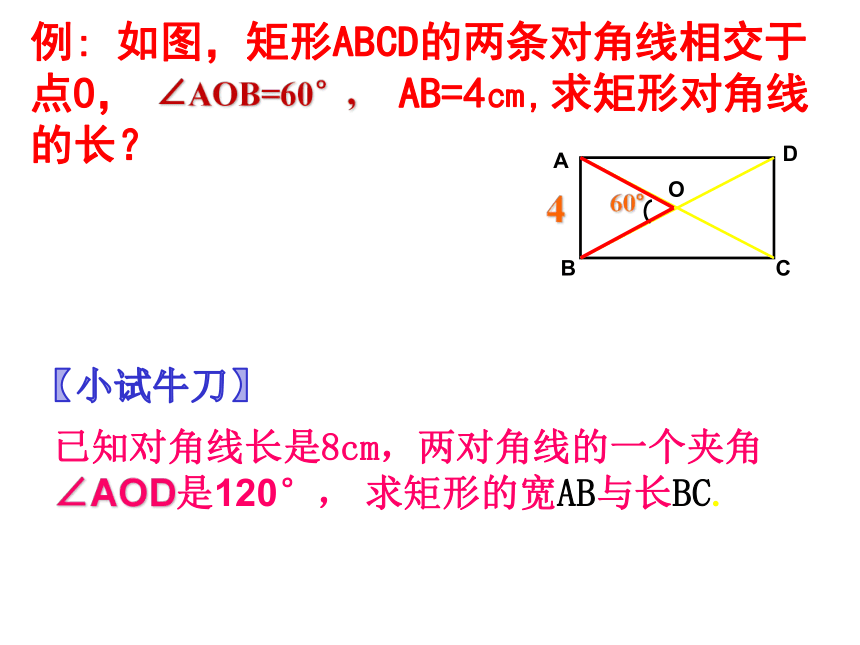
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC.
60°
4
∠AOB=60°,
【小试牛刀】
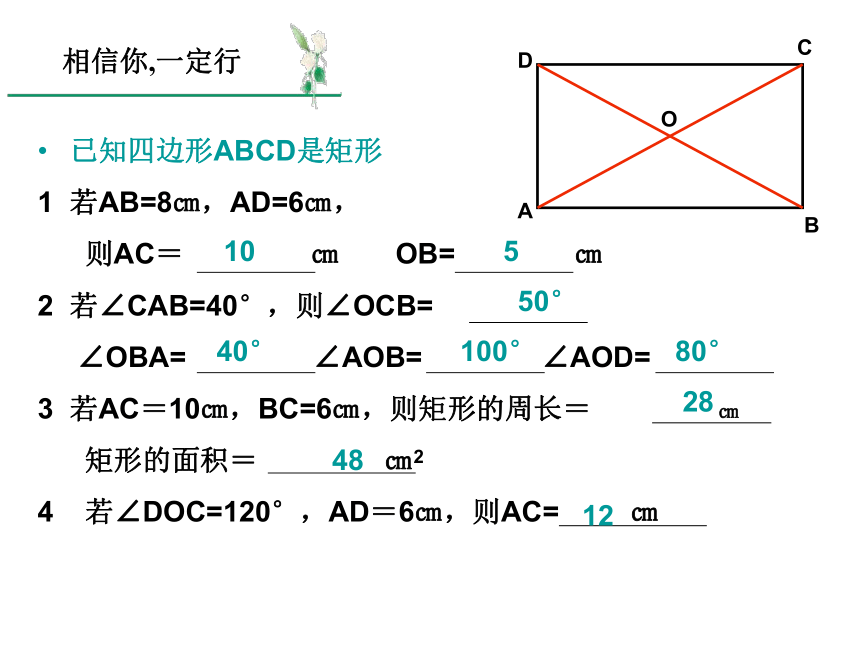
已知四边形ABCD是矩形
若AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
相信你,一定行
1、矩形的四个角都是直角.
※ 矩形的性质定理
2、矩形的对角线相等.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
这节课你学到了什么
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半
还有什么困惑吗?
18.2.1 矩形
(第2课时)
一、回忆
1.等腰三角形和等边三角形具有怎样的关系?
2.如何将等腰三角形这个图形转化为等边三角形?
角
边
特殊化
二、探究
如果将平行四边形的角、边进行特殊化的变形,会?
角
特殊化
矩形的定义:
有一个角是直角的平行四边形是矩形
矩形的性质
两组对边分别相等
两组对边分别平行
两组对角分别相等
对角线互相平分
矩形有没有平行四边形不具有的特殊的性质呢?
猜想:矩形的四个角都是直角
猜想:矩形的对角线相等
三、证明猜想
猜想:矩形的四个角都是直角
画图
写已知
写求证
推理证明
A
D
C
B
已知: 矩形ABCD
求证: ∠A=∠B=∠C=∠D=90°
矩形的性质:矩形的四个角都是直角
题设:
结论:
如果一个四边形是矩形
那么这个矩形的四个角都是直角
数学符号语言:
A
D
C
B
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
三、证明猜想
猜想:矩形的对角线相等
已知: 矩形ABCD,连接AC,BD,相交于点O
求证: AC=BD
A
D
C
B
O
矩形的性质:矩形的对角线相等
题设:
结论:
如果一个四边形是矩形
那么这个矩形的对角线相等
∵四边形ABCD是矩形
∴AC=BD
数学符号语言:
B
A
D
C
O
四、探究
A
D
C
B
O
AO是直角三角形斜边的中线
还有哪条线段是哪个直角三角形斜边的中线?
猜想:AO与BD有什么关系?
猜想:直角三角形斜边的中线等于斜边的一半
A
D
C
B
O
已知: 矩形ABCD,连接AC,BD,相交于点O
求证:
直角三角形的性质:直角三角形斜边的中线等于斜边的一半
题设:
结论:
如果一个三角形是直角三角形
那么斜边的中线等于斜边的一半
数学符号语言:
B
A
C
O
∵ Rt▲ABC,O为BC中点,连接AO
∴
课后小结
本节课我们学习了矩形的哪些性质?
谢谢!
18.2.1 矩形
(第1课时)
温故而知新
边 角 对角线
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
一个角是
直角
平行
四边形
矩形
有一个角是直角的平行四边形叫做矩形
生活中的实例
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
观察内角和对角线的变化
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形∠A=90°
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵矩形ABCD是平行四边形
又∵ ∠A=90°
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
求证:矩形的对角线相等
A
D
C
B
已知:矩形ABCD,
求证:AC=BD
证明一:
∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB
∴AC=BD
证明二:
∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°, AB=CD
∴AC2=AB2+BC2,BD2=CD2+BC2
∴AC=BD
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC.
60°
4
∠AOB=60°,
【小试牛刀】
已知四边形ABCD是矩形
若AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
相信你,一定行
1、矩形的四个角都是直角.
※ 矩形的性质定理
2、矩形的对角线相等.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
这节课你学到了什么
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半
还有什么困惑吗?
18.2.1 矩形
(第2课时)
一、回忆
1.等腰三角形和等边三角形具有怎样的关系?
2.如何将等腰三角形这个图形转化为等边三角形?
角
边
特殊化
二、探究
如果将平行四边形的角、边进行特殊化的变形,会?
角
特殊化
矩形的定义:
有一个角是直角的平行四边形是矩形
矩形的性质
两组对边分别相等
两组对边分别平行
两组对角分别相等
对角线互相平分
矩形有没有平行四边形不具有的特殊的性质呢?
猜想:矩形的四个角都是直角
猜想:矩形的对角线相等
三、证明猜想
猜想:矩形的四个角都是直角
画图
写已知
写求证
推理证明
A
D
C
B
已知: 矩形ABCD
求证: ∠A=∠B=∠C=∠D=90°
矩形的性质:矩形的四个角都是直角
题设:
结论:
如果一个四边形是矩形
那么这个矩形的四个角都是直角
数学符号语言:
A
D
C
B
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
三、证明猜想
猜想:矩形的对角线相等
已知: 矩形ABCD,连接AC,BD,相交于点O
求证: AC=BD
A
D
C
B
O
矩形的性质:矩形的对角线相等
题设:
结论:
如果一个四边形是矩形
那么这个矩形的对角线相等
∵四边形ABCD是矩形
∴AC=BD
数学符号语言:
B
A
D
C
O
四、探究
A
D
C
B
O
AO是直角三角形斜边的中线
还有哪条线段是哪个直角三角形斜边的中线?
猜想:AO与BD有什么关系?
猜想:直角三角形斜边的中线等于斜边的一半
A
D
C
B
O
已知: 矩形ABCD,连接AC,BD,相交于点O
求证:
直角三角形的性质:直角三角形斜边的中线等于斜边的一半
题设:
结论:
如果一个三角形是直角三角形
那么斜边的中线等于斜边的一半
数学符号语言:
B
A
C
O
∵ Rt▲ABC,O为BC中点,连接AO
∴
课后小结
本节课我们学习了矩形的哪些性质?
谢谢!
