17.1.1 变量与函数(2) 课件(共26张PPT)
文档属性
| 名称 | 17.1.1 变量与函数(2) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
2022年春华师大版数学
八年级下册数学精品课件
17.1.1 变量与函数(2)
学习目标
会根据函数表达式求函数值.
能根据实际问题写出函数表达式.
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
在同一个变化过程中,理解变量与常量的关键词:发生了变化和始终不变.
复习回顾
一般地,在一个变化过程中有两个变量x与y,如果对于x的每 一个值, y都有唯一的值与它对应,那么就说x是自变量, y是因变量, 此时也称 y是x的函数.
函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
在数学中,“y是x的函数”这句话常用 y = x的代数式来表示,这里x是自变量,y是x的函数.
复习回顾
函数关系的三种表示方法
解析法、列表法、图象法
(1)解析法,如问题3中的f= ,问题4中的S=πr2,这些表达式称为函数的关系式.
(2)列表法,如问题2中的表格,问题3中的波长与频率关系表.
(3)图象法,问题1中的气温曲线.
复习回顾
1.函数的关系式是等式.
2.通常等式的右边是含有自变量的代数式,左边的一个字母表示函数.
函数的书写:
书写函数关系式的一般步骤:
1.先认真审题,根据题意找出相等关系;
2.按相等关系,写出含有两个变量的等式;
3.将等式变形为用含有自变量的代数式表示函数的式子.
复习回顾
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
问题1:填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能
发现什么
问题引入
我们发现,横向的加数与纵向的加数之和为10.
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
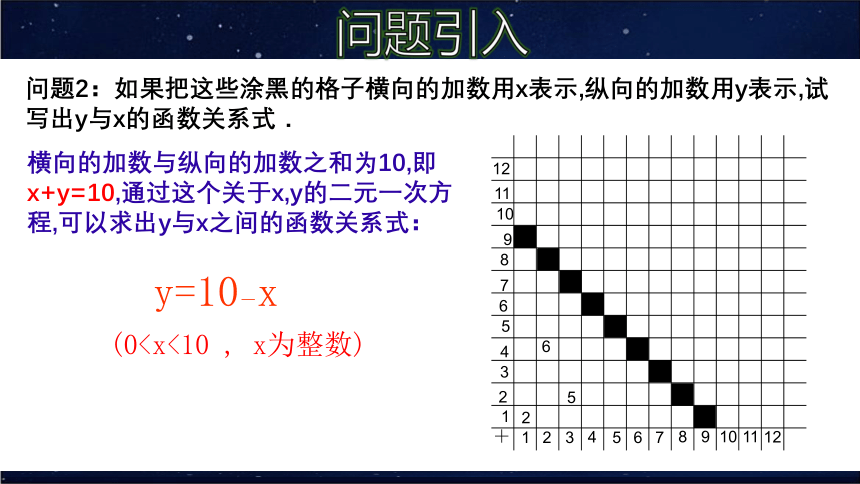
问题2:如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试
写出y与x的函数关系式.
问题引入
横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式:
y=10-x
(01
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
问题3:当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加
数为6时,横向的加数为多少?
问题引入
把x=3代入y=10-x中,得:y=7.
所以纵向的加数是7.
把y=6代入y=10-x中,得:x=4.
所以横向的加数是4.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
把自变量x的值带入关系式中,即可求出函数的值.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7.
(2)令 解得x=
即当x= 时,y=0.
针对练习
例1 试写出等腰三角形中顶角的度数y与底角的度数x之间的函数
关系式.
【分析】根据等腰三角形两个底角相等的性质,以及三角形内角和为180度,可以得到关于x,y的二元一次方程:2x+y=180
利用变量之间的关系列出方程,再把方程变形,从而求出两个变量之间的函数关系.
方程变形为:
y=180-2x
(0典例解析
例2 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式;
(2)当MA=1cm时,重叠部分的面积是多少?
分析:(1)根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系;
(2)将x=1cm代入可得出重叠部分的面积.
典例解析
解:(1)由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,
两图形重合的长度为AM=x,
,0<x≤10,
M
Q
N
P
A
B
C
X
X
典例解析
(2)当MA=1cm时,重叠部分的面积是:
如果把题目改为“最后C与N重合,重合的图形面积y与x的关系式会怎样”?请自己动手画画
Q
N
P
A
B
C
X
X-10
M
拓展延伸
1.对于一些简单问题的函数表达式,往往可以通过利用已有的公式列出.
2.一些实际问题的函数表达式
例如:底边一定,三角形的面积随高的变化而变化.
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
总结提升
1.求下列函数中自变量x的取值范围:
.
1
.
0
.
-1
x取全体实数
达标检测
2.当x=2及x=-3时,分别求出下列函数的函数值:
y=(x+1)(x-2);(2)y=2x2-3x+2; (3)
.
解:(1)x=2,y=0;x=-3,y=10
解:(2)x=2,y=4;x=-3,y=29
解:(3)x=2,y=4;x=-3,y=1/4
y=
x+2
x-1
达标检测
3.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少?
解:t=8时,代入s=10t+2t2,得s=208
答:坡长为208米.
达标检测
4.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
达标检测
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
八年级下册数学精品课件
17.1.1 变量与函数(2)
学习目标
会根据函数表达式求函数值.
能根据实际问题写出函数表达式.
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
在同一个变化过程中,理解变量与常量的关键词:发生了变化和始终不变.
复习回顾
一般地,在一个变化过程中有两个变量x与y,如果对于x的每 一个值, y都有唯一的值与它对应,那么就说x是自变量, y是因变量, 此时也称 y是x的函数.
函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
在数学中,“y是x的函数”这句话常用 y = x的代数式来表示,这里x是自变量,y是x的函数.
复习回顾
函数关系的三种表示方法
解析法、列表法、图象法
(1)解析法,如问题3中的f= ,问题4中的S=πr2,这些表达式称为函数的关系式.
(2)列表法,如问题2中的表格,问题3中的波长与频率关系表.
(3)图象法,问题1中的气温曲线.
复习回顾
1.函数的关系式是等式.
2.通常等式的右边是含有自变量的代数式,左边的一个字母表示函数.
函数的书写:
书写函数关系式的一般步骤:
1.先认真审题,根据题意找出相等关系;
2.按相等关系,写出含有两个变量的等式;
3.将等式变形为用含有自变量的代数式表示函数的式子.
复习回顾
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
问题1:填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能
发现什么
问题引入
我们发现,横向的加数与纵向的加数之和为10.
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
问题2:如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试
写出y与x的函数关系式.
问题引入
横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式:
y=10-x
(0
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
问题3:当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加
数为6时,横向的加数为多少?
问题引入
把x=3代入y=10-x中,得:y=7.
所以纵向的加数是7.
把y=6代入y=10-x中,得:x=4.
所以横向的加数是4.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
把自变量x的值带入关系式中,即可求出函数的值.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7.
(2)令 解得x=
即当x= 时,y=0.
针对练习
例1 试写出等腰三角形中顶角的度数y与底角的度数x之间的函数
关系式.
【分析】根据等腰三角形两个底角相等的性质,以及三角形内角和为180度,可以得到关于x,y的二元一次方程:2x+y=180
利用变量之间的关系列出方程,再把方程变形,从而求出两个变量之间的函数关系.
方程变形为:
y=180-2x
(0
例2 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式;
(2)当MA=1cm时,重叠部分的面积是多少?
分析:(1)根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系;
(2)将x=1cm代入可得出重叠部分的面积.
典例解析
解:(1)由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,
两图形重合的长度为AM=x,
,0<x≤10,
M
Q
N
P
A
B
C
X
X
典例解析
(2)当MA=1cm时,重叠部分的面积是:
如果把题目改为“最后C与N重合,重合的图形面积y与x的关系式会怎样”?请自己动手画画
Q
N
P
A
B
C
X
X-10
M
拓展延伸
1.对于一些简单问题的函数表达式,往往可以通过利用已有的公式列出.
2.一些实际问题的函数表达式
例如:底边一定,三角形的面积随高的变化而变化.
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
总结提升
1.求下列函数中自变量x的取值范围:
.
1
.
0
.
-1
x取全体实数
达标检测
2.当x=2及x=-3时,分别求出下列函数的函数值:
y=(x+1)(x-2);(2)y=2x2-3x+2; (3)
.
解:(1)x=2,y=0;x=-3,y=10
解:(2)x=2,y=4;x=-3,y=29
解:(3)x=2,y=4;x=-3,y=1/4
y=
x+2
x-1
达标检测
3.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少?
解:t=8时,代入s=10t+2t2,得s=208
答:坡长为208米.
达标检测
4.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
达标检测
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
达标检测
https://www.21cnjy.com/help/help_extract.php
