17.2.1 平面直角坐标系 课件(共28张PPT)
文档属性
| 名称 | 17.2.1 平面直角坐标系 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 17:32:34 | ||
图片预览







文档简介
(共28张PPT)
2022年春华师大版数学
八年级下册数学精品课件
17.2.1 平面直角坐标系
学习目标
理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系.
理解各象限内及坐标轴上点的坐标特征;会用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
如果课上老师要点一名同学回答问题,但不知道同学们的姓名,我想根据同学们所在的位置来确定,你能帮我解决吗?
情境引入
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
知识精讲
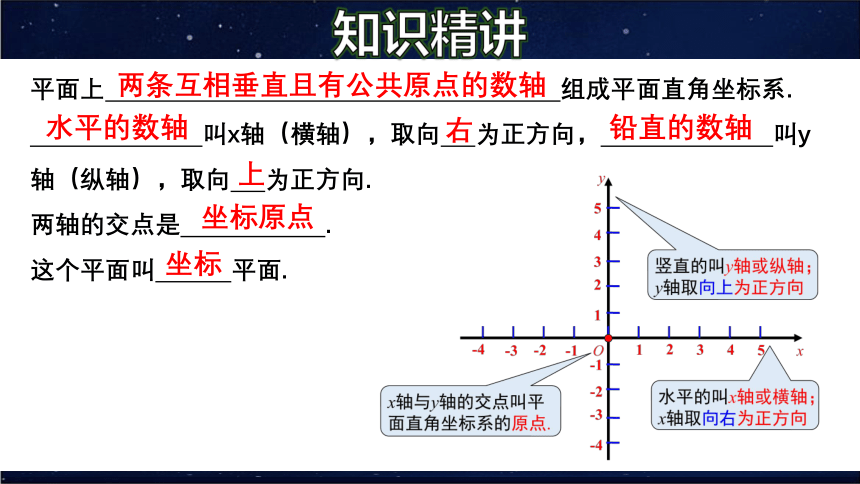
平面上 组成平面直角坐标系.
叫x轴(横轴),取向 为正方向, 叫y轴(纵轴),取向 为正方向.
两轴的交点是 .
这个平面叫 平面.
两条互相垂直且有公共原点的数轴
水平的数轴
右
上
铅直的数轴
坐标原点
坐标
知识精讲
两条数轴:(一般性特征)
(1)互相垂直(其它坐标系不一定要求)
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
平面直角坐标系具有哪些特征呢?
O
X
Y
-4 -3 -2 -1 1 2 3 4
4
3
2
1
-1
-2
-3
-4
知识精讲
下面四个图形中,是平面直角坐标系的是( )
D
针对练习
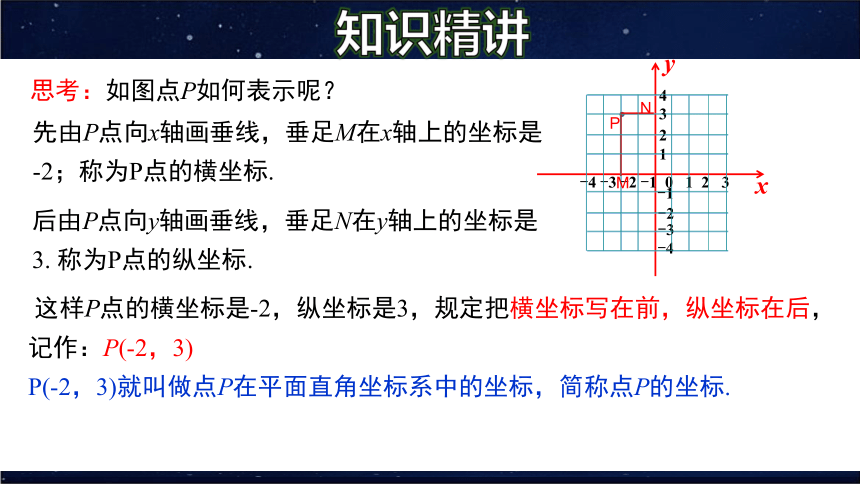
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
知识精讲
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
o
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
针对练习
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
针对练习
A
B
C
E
F
D
例1 写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
典例解析
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
针对练面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
知识精讲
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
知识精讲
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2:观察坐标系,填写坐标轴上的点的坐标的特征:
知识精讲
问题:坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
知识精讲
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
1.描出A(3,2) B(3,-2)C(-3,2)D(-3,-2)并指出所在象限
2.写出图中 M、N、O、P 的坐标
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·M
·N
·
·
·
·O
·P
(4,4)
(-4,4)
(-2,0)
(0,3)
针对练习
若点在第一、三象限角平分线上或者在第二、四象限角平分线上,它的横、纵坐标有什么特点?
(4,4)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
·O
·P
(-4,4)
在第一、三象限角平分线上,它的横坐标等于纵坐标
在第二、四象限角平分线上,它的横坐标与纵坐标互为相反数.
知识精讲
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
·
·N
1.在四个象限内的点的坐标各有什么特征?
2.两条坐标轴上的点的坐标各有什么特征?
X轴上的点纵坐标等于0,表示为(x,0)
Y轴上的点横坐标等于0,表示为(0,y)
(-2,0)
M(0,3)
·O
·R
( 2 , 0 )
( 0 , -3 )
知识精讲
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
在直角坐标系中描出点A(3,2),分别找出它关于X轴,Y轴及原点的对称点,并写出这些点的坐标.
1.关于X轴对称的两点,横坐标相等,纵坐标互为相反数;
2.关于Y轴对称的两点,横坐标互为相反数,纵坐标相等;
3.关于原点对称的两点,横坐标、纵坐标互为相反数.
知识精讲
3.如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限 C.第二象限 D.第一象限
D
4.直角坐标系中有一点 M(a,b),其中ab=0 ,则 点M的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
D
5.长方形ABCD中,三点的坐标分别是(0,0),(5,0), (5,3), D点的坐标( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)
C
1.已知点P( -3 , 2 ),说出点P位置在_______象限.
2.已知点Q(0,-3),说出点Q的位置在_______.
第二
y轴
达标检测
达标检测
6.点A(2,-3)关于x轴对称点的坐标为 .关于y轴对称点的坐标为 .关于原点对称点的坐标为 .
(2,3)
(-2,-3)
(-2,3)
7.点(3,5)与点(3,-5)关于________轴对称.
X
8.点A关于原点对称点的坐标为(2,3),则点A 关于 y 轴对称点的坐标为 .
(2,-3)
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴
x 轴上负半轴
原点
9.下列各点分别在坐标平面的什么位置上?
达标检测
11.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
12.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .
3
(5,-4)
-1
10.已知a二
达标检测
小结梳理
1.平面直角坐标系的有关概念及画法;
2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;
3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;
4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
八年级下册数学精品课件
17.2.1 平面直角坐标系
学习目标
理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系.
理解各象限内及坐标轴上点的坐标特征;会用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
如果课上老师要点一名同学回答问题,但不知道同学们的姓名,我想根据同学们所在的位置来确定,你能帮我解决吗?
情境引入
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
知识精讲
平面上 组成平面直角坐标系.
叫x轴(横轴),取向 为正方向, 叫y轴(纵轴),取向 为正方向.
两轴的交点是 .
这个平面叫 平面.
两条互相垂直且有公共原点的数轴
水平的数轴
右
上
铅直的数轴
坐标原点
坐标
知识精讲
两条数轴:(一般性特征)
(1)互相垂直(其它坐标系不一定要求)
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
平面直角坐标系具有哪些特征呢?
O
X
Y
-4 -3 -2 -1 1 2 3 4
4
3
2
1
-1
-2
-3
-4
知识精讲
下面四个图形中,是平面直角坐标系的是( )
D
针对练习
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
知识精讲
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
o
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
针对练习
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
针对练习
A
B
C
E
F
D
例1 写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
典例解析
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
针对练面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
知识精讲
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
知识精讲
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2:观察坐标系,填写坐标轴上的点的坐标的特征:
知识精讲
问题:坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
知识精讲
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
1.描出A(3,2) B(3,-2)C(-3,2)D(-3,-2)并指出所在象限
2.写出图中 M、N、O、P 的坐标
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·M
·N
·
·
·
·O
·P
(4,4)
(-4,4)
(-2,0)
(0,3)
针对练习
若点在第一、三象限角平分线上或者在第二、四象限角平分线上,它的横、纵坐标有什么特点?
(4,4)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
·O
·P
(-4,4)
在第一、三象限角平分线上,它的横坐标等于纵坐标
在第二、四象限角平分线上,它的横坐标与纵坐标互为相反数.
知识精讲
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
·
·N
1.在四个象限内的点的坐标各有什么特征?
2.两条坐标轴上的点的坐标各有什么特征?
X轴上的点纵坐标等于0,表示为(x,0)
Y轴上的点横坐标等于0,表示为(0,y)
(-2,0)
M(0,3)
·O
·R
( 2 , 0 )
( 0 , -3 )
知识精讲
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
在直角坐标系中描出点A(3,2),分别找出它关于X轴,Y轴及原点的对称点,并写出这些点的坐标.
1.关于X轴对称的两点,横坐标相等,纵坐标互为相反数;
2.关于Y轴对称的两点,横坐标互为相反数,纵坐标相等;
3.关于原点对称的两点,横坐标、纵坐标互为相反数.
知识精讲
3.如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限 C.第二象限 D.第一象限
D
4.直角坐标系中有一点 M(a,b),其中ab=0 ,则 点M的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
D
5.长方形ABCD中,三点的坐标分别是(0,0),(5,0), (5,3), D点的坐标( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)
C
1.已知点P( -3 , 2 ),说出点P位置在_______象限.
2.已知点Q(0,-3),说出点Q的位置在_______.
第二
y轴
达标检测
达标检测
6.点A(2,-3)关于x轴对称点的坐标为 .关于y轴对称点的坐标为 .关于原点对称点的坐标为 .
(2,3)
(-2,-3)
(-2,3)
7.点(3,5)与点(3,-5)关于________轴对称.
X
8.点A关于原点对称点的坐标为(2,3),则点A 关于 y 轴对称点的坐标为 .
(2,-3)
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴
x 轴上负半轴
原点
9.下列各点分别在坐标平面的什么位置上?
达标检测
11.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
12.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .
3
(5,-4)
-1
10.已知a
达标检测
小结梳理
1.平面直角坐标系的有关概念及画法;
2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;
3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;
4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.
https://www.21cnjy.com/help/help_extract.php
