17.3.2 一次函数的图象 课件(共24张PPT)
文档属性
| 名称 | 17.3.2 一次函数的图象 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 14:56:24 | ||
图片预览





文档简介
2022年春华师大版数学
八年级下册数学精品课件
17.3.2 一次函数的图象
学习目标
会利用描点法画一次函数的图象;通过观察归纳出两点法画一次函数图象.
通过一次函数图象总结出图象平移规律并应用解题.
1
2
3
1
0
4
3
2
–2
–1
–1
–2
–3
–3
5
y
x
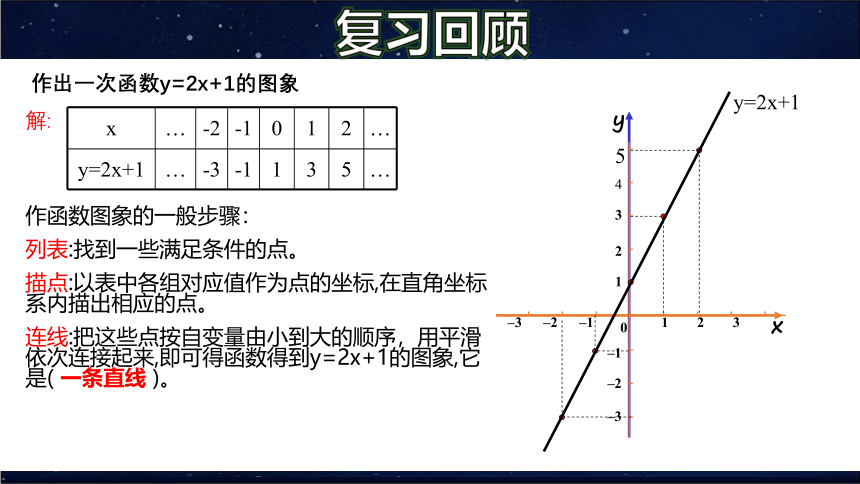
作出一次函数y=2x+1的图象
解:
x
…
-2
-1
0
1
2
…
y=2x+1
…
-3
-1
1
3
5
…
作函数图象的一般步骤:
列表:找到一些满足条件的点。
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:把这些点按自变量由小到大的顺序,用平滑依次连接起来,即可得函数得到y=2x+1的图象,它是( 一条直线 )。
y=2x+1
复习回顾
在平面直角坐标系中画出下列函数的图像:
(1) (2) (3) (4)
知识精讲
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
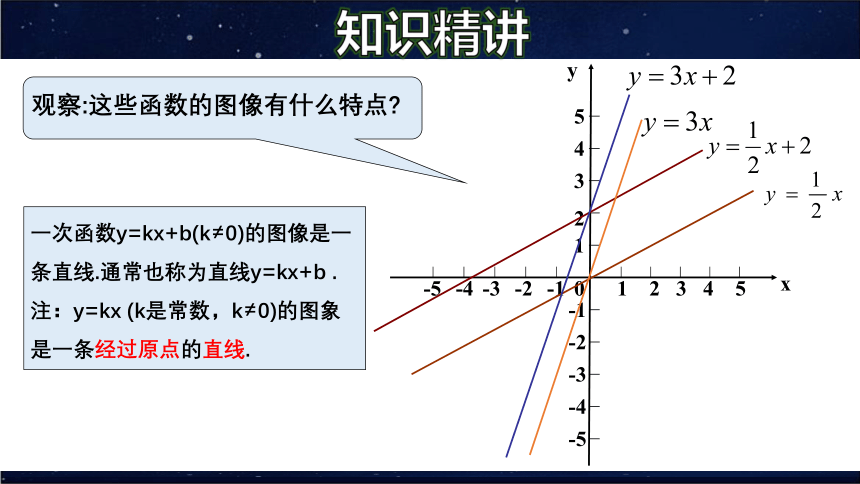
观察:这些函数的图像有什么特点?
x
y
知识精讲
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
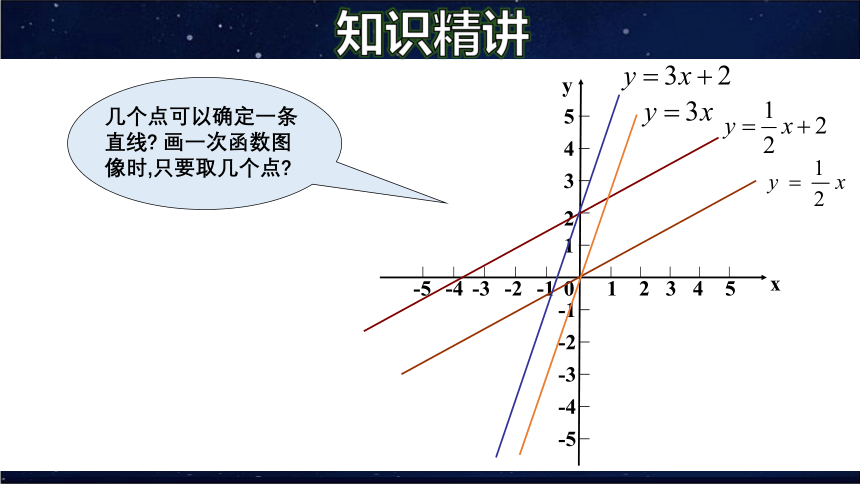
几个点可以确定一条直线? 画一次函数图像时,只要取几个点?
y
x
知识精讲
由于两点确定一条直线,
(1)画 y=kx 的图象只需描点(0,b)和点 (1,k),连线即可.
(2) 画 y=kx +b图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
知识精讲
两点法:
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
y
x
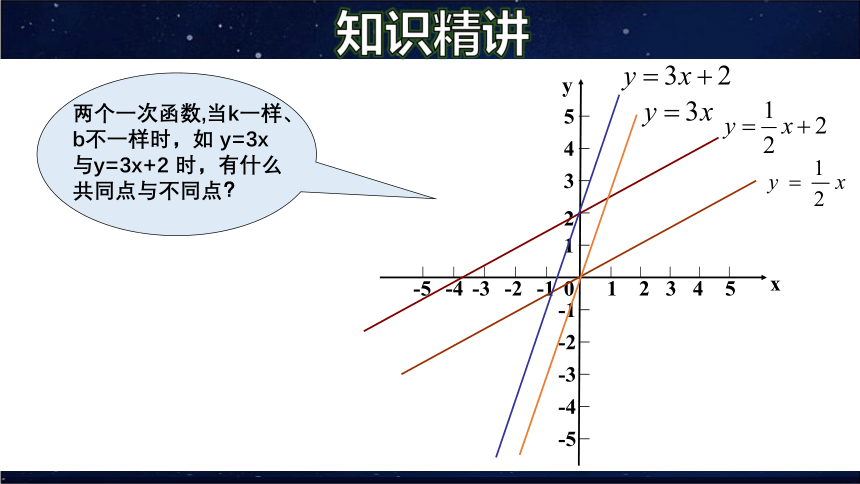
两个一次函数,当k一样、b不一样时,如 y=3x 与y=3x+2 时,有什么共同点与不同点?
知识精讲
(3)函数 y=3x 的图象经过 ,函数y= 3x+2的图像与y轴交于点( ),即它可以看作由直线 y1=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,2
上
2
一条直线
相同
知识精讲
(2)在同一直角坐标系中,直线 y =3x与 y =3x+2的位置关系是_______.
平行
x
y
2
0
.
.
.
.
例1 在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象.
.
y=x
.
y=x+2
y=x-2
典例解析
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
y=x
y=x+2
y=x-2
0
1
2
3
-2
-1
(1)这几个函数的图象形状都是 并且倾斜程度______即相互平行.
(2)函数y=x的图象经过(0,0),函数y=x+2的图象与y轴交于点_________,即它可以看作由直线y=x向_____平移______个单位长度而得到.
(3)函数y=x-2的图象与y轴交于点________,即它可以看作由直线y=x向_____平移_____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
典例解析
x
y
2
0
.
.
.
.
请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
针对练习
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
知识精讲
思考:一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
例2 小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则s与t的函数关系式为___________________________________________________________________
s=570-95t
问题:画出上述问题中小明距北京的路程s 与开车时间t 之间函数s=570-95t的图象.
典例解析
这里s和t取的值悬殊较大,怎么办?
分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图):
讨 论: (1)这个函数是不是一次函数?
(2)这个函数中自变量t的取值范围是什么?函数的图象是什么?
(3)在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形?你能不能找出几个例子加以说明?
典例解析
1.直线y=4x-3过点(___,0)、(0,___)?
2.直线 过点(___,0)、(0,__)
-3
6
2
3.直线y=5x+2与x轴的交点A的坐标为 ,与y轴的交点B的坐标为 。
4.直线y=-2x+6呢?
(3,0)、(0,6)
5.直线y=kx+b呢?
(0,b)
达标检测
6.拖拉机开始工作时,油箱中有油24L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
D
达标检测
7.(1)在同一直角坐标系画一次函数 y =-6x与y =-6x +5的图象.
(2)一次函数y =-6x +5的图象与y轴交于点 ,
可以看作由直线 y =-6x向 平移 个单位长度而得到.
(3)在同一直角坐标系中,直线 y =-6x +5与 y =-6x的位置关系是 .
上
5
(0,5)
平行
达标检测
8.已知直线y=kx+5与直线y=3x-7平行则k= .
变式一:已知直线y=(3k-5)x+7与直线y=-2x+9平行,则k= .
变式二:已知直线y=(a+3)x-5与直线y=(15-2a)x+4平行,则a= .
3
解:∵3k-5=-2, ∴3k=3,即k=1
1
解: ∵a+3=15-2a,
∴3a=12,即a=4.
4
达标检测
令y=0, 得 x-1=0, 解得x=2
1
2
9.直线y =????????x - 1与两坐标轴围成的三角形的面积是多少?
?
解: 令x=0, 得y = -1
∴直线经过点(0,-1)、(2,0)
-1
2
-1
-2
1
1
x
y
2
3
-2
-3
∴S = × 2×1 = 1
1
2
达标检测
直线y=kx+b与x轴的交点坐标为 与y轴的交点坐标为 .
(0,b)
若直线y1=k1x+b1与直y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立.
小结梳理
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
https://www.21cnjy.com/help/help_extract.php
八年级下册数学精品课件
17.3.2 一次函数的图象
学习目标
会利用描点法画一次函数的图象;通过观察归纳出两点法画一次函数图象.
通过一次函数图象总结出图象平移规律并应用解题.
1
2
3
1
0
4
3
2
–2
–1
–1
–2
–3
–3
5
y
x
作出一次函数y=2x+1的图象
解:
x
…
-2
-1
0
1
2
…
y=2x+1
…
-3
-1
1
3
5
…
作函数图象的一般步骤:
列表:找到一些满足条件的点。
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:把这些点按自变量由小到大的顺序,用平滑依次连接起来,即可得函数得到y=2x+1的图象,它是( 一条直线 )。
y=2x+1
复习回顾
在平面直角坐标系中画出下列函数的图像:
(1) (2) (3) (4)
知识精讲
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
观察:这些函数的图像有什么特点?
x
y
知识精讲
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
几个点可以确定一条直线? 画一次函数图像时,只要取几个点?
y
x
知识精讲
由于两点确定一条直线,
(1)画 y=kx 的图象只需描点(0,b)和点 (1,k),连线即可.
(2) 画 y=kx +b图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
知识精讲
两点法:
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
y
x
两个一次函数,当k一样、b不一样时,如 y=3x 与y=3x+2 时,有什么共同点与不同点?
知识精讲
(3)函数 y=3x 的图象经过 ,函数y= 3x+2的图像与y轴交于点( ),即它可以看作由直线 y1=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,2
上
2
一条直线
相同
知识精讲
(2)在同一直角坐标系中,直线 y =3x与 y =3x+2的位置关系是_______.
平行
x
y
2
0
.
.
.
.
例1 在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象.
.
y=x
.
y=x+2
y=x-2
典例解析
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
y=x
y=x+2
y=x-2
0
1
2
3
-2
-1
(1)这几个函数的图象形状都是 并且倾斜程度______即相互平行.
(2)函数y=x的图象经过(0,0),函数y=x+2的图象与y轴交于点_________,即它可以看作由直线y=x向_____平移______个单位长度而得到.
(3)函数y=x-2的图象与y轴交于点________,即它可以看作由直线y=x向_____平移_____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
典例解析
x
y
2
0
.
.
.
.
请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
针对练习
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
知识精讲
思考:一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
例2 小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则s与t的函数关系式为___________________________________________________________________
s=570-95t
问题:画出上述问题中小明距北京的路程s 与开车时间t 之间函数s=570-95t的图象.
典例解析
这里s和t取的值悬殊较大,怎么办?
分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图):
讨 论: (1)这个函数是不是一次函数?
(2)这个函数中自变量t的取值范围是什么?函数的图象是什么?
(3)在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形?你能不能找出几个例子加以说明?
典例解析
1.直线y=4x-3过点(___,0)、(0,___)?
2.直线 过点(___,0)、(0,__)
-3
6
2
3.直线y=5x+2与x轴的交点A的坐标为 ,与y轴的交点B的坐标为 。
4.直线y=-2x+6呢?
(3,0)、(0,6)
5.直线y=kx+b呢?
(0,b)
达标检测
6.拖拉机开始工作时,油箱中有油24L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
D
达标检测
7.(1)在同一直角坐标系画一次函数 y =-6x与y =-6x +5的图象.
(2)一次函数y =-6x +5的图象与y轴交于点 ,
可以看作由直线 y =-6x向 平移 个单位长度而得到.
(3)在同一直角坐标系中,直线 y =-6x +5与 y =-6x的位置关系是 .
上
5
(0,5)
平行
达标检测
8.已知直线y=kx+5与直线y=3x-7平行则k= .
变式一:已知直线y=(3k-5)x+7与直线y=-2x+9平行,则k= .
变式二:已知直线y=(a+3)x-5与直线y=(15-2a)x+4平行,则a= .
3
解:∵3k-5=-2, ∴3k=3,即k=1
1
解: ∵a+3=15-2a,
∴3a=12,即a=4.
4
达标检测
令y=0, 得 x-1=0, 解得x=2
1
2
9.直线y =????????x - 1与两坐标轴围成的三角形的面积是多少?
?
解: 令x=0, 得y = -1
∴直线经过点(0,-1)、(2,0)
-1
2
-1
-2
1
1
x
y
2
3
-2
-3
∴S = × 2×1 = 1
1
2
达标检测
直线y=kx+b与x轴的交点坐标为 与y轴的交点坐标为 .
(0,b)
若直线y1=k1x+b1与直y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立.
小结梳理
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
https://www.21cnjy.com/help/help_extract.php
