17.5 实践与探索 课件(23张ppt)
文档属性
| 名称 | 17.5 实践与探索 课件(23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览






文档简介
2022年春华师大版数学
八年级下册数学精品课件
17.5 实践与探索
学习目标
能根据一次函数的图象求二元一次方程组的解.
能通过数形结合说出一次函数与一元一次方程及一元一次不等式的联系.
会图象上获取信息的能力,利用数形结合解决实际问题.
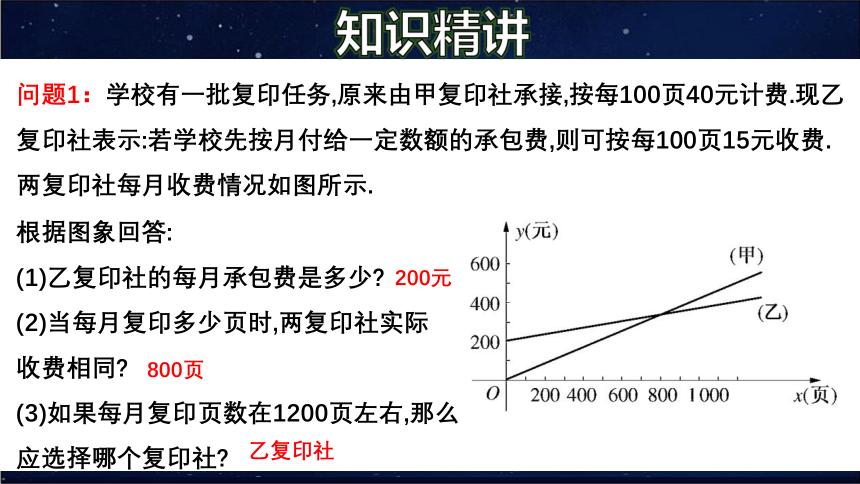
问题1:学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙
复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.
两复印社每月收费情况如图所示.
根据图象回答:
(1)乙复印社的每月承包费是多少?
(2)当每月复印多少页时,两复印社实际
收费相同?
(3)如果每月复印页数在1200页左右,那么
应选择哪个复印社?
200元
800页
乙复印社
知识精讲
问题1:学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙
复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.
两复印社每月收费情况如图所示.
知识精讲
要点归纳:
由函数图象解答问题时,首先要明确横、纵轴表示的含义,函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定范围内,位于上方图象的函数值要比位于下方的图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确,观察得越仔细,所得的值就越准确.
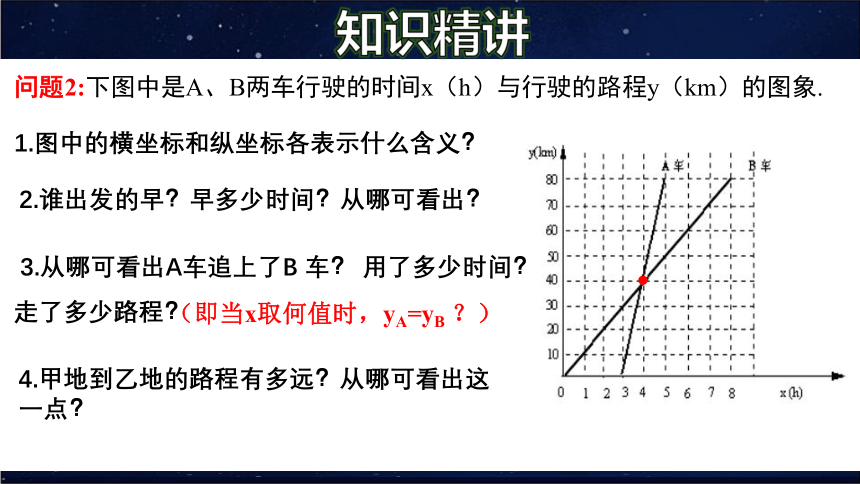
知识精讲
2.谁出发的早?早多少时间?从哪可看出?
3.从哪可看出A车追上了B 车? 用了多少时间?
走了多少路程?
4.甲地到乙地的路程有多远?从哪可看出这一点?
1.图中的横坐标和纵坐标各表示什么含义?
·
(即当x取何值时,yA=yB ?)
知识精讲
问题2:下图中是A、B两车行驶的时间x(h)与行驶的路程y(km)的图象.
5.在4小时以前,哪车在前?
在4小时以后,哪车在前 ?
从图上怎么看?
6.你能从图上看出哪车的速度快?两条直线的倾斜程度表示了什么意义?
7.两车行驶的路程分别用yA、 yB表示, yA、 yB(km)与时间 x(h)之间的函数关系式分别是什么?
(即当x取何值时,yA>yB?)
(即当x取何值时,yA知识精讲
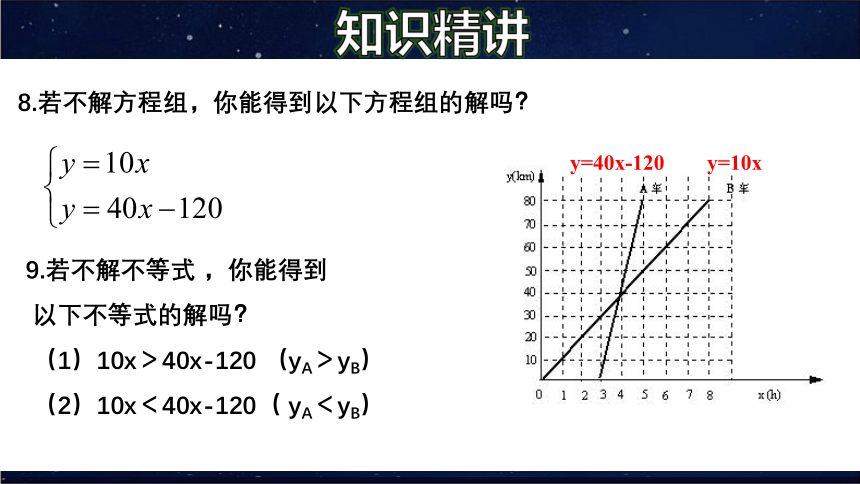
y=10x
y=40x-120
8.若不解方程组,你能得到以下方程组的解吗?
9.若不解不等式 ,你能得到
以下不等式的解吗?
(1)10x>40x-120 (yA>yB)
(2)10x<40x-120( yA<yB)
知识精讲
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而两个一次函数的关系式就是方程组中的两个方程,所以交点的坐标就是方程组的解.
据此,我们可以利用图象来求某些方程组的解以及不等式的解集.
·
知识精讲
解:由x-2y=-2,可得y=12????+1
?
在同一直角坐标系内作出一次函数y=12????+1 的图象l1和y=2x-2的图象l2,如图所示
?
例1 用图象法解方程组
所以方程组?????2????=?22?????????=2 的解是????=2????=2
?
同理,由2x-y=2,可得y=2x-2
得l1,l2的交点为P(2,2).
典例解析
例2 利用图象解不等式:
(1)2x-5>-x+1, (2) 2x-5<-x+1.
解:设y1=2x-5,y2=-x+1,
在直角坐标系中画出这两条直线,如图.
两条直线的交点坐标是(2, -1) ,可知:
(1)2x--5>-x+1的解集是y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2.
典例解析
1.从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题的方法?
1) 图象法;2)数形结合法.
2.在观察图形时主要看图形中的哪几个关键地方?
1) 两坐标轴的含义;2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.
3.利用函数的图象我们刚才解决了哪几个问题?
1)求方程组的交点坐标;2)求不等式的解集.
总结提升
用图象法解二元一次方程组的具体方法:
1.先把两方程转化成y=kx+b 的形式;
2.在同一坐标系中画出两函数的图象;
3.找两函数的交点坐标,交点坐标即是方程组的解.
总结提升
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗?
(2)问43码的鞋相当于多少厘米的鞋?
x(厘米)
23
23.5
24.5
25.5
26
……
y(码)
36
37
39
41
42
……
针对练习
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画
出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
x (厘米)
y(码)
23
23.5
24
O
40
36
41
37
38
39
24.5
25.5
25
26
26.5
27
42
针对练习
解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得
所以y与x的函数关系式可能是:y=2x-10
(2)当y=43时,2x-10=43,
解得x=26.5.
针对练习
1.直线y=x+3与x轴的交点坐标为 ,所以相应的方程x+3=0的解是 .
2.设m,n为常数且m≠0,直线y=mx+n(如图所示),则方程mx+n=0的解是 .
3.对于y1=2x-1, y2=4x-2,下列说法:
①两直线平行; ②两直线交y轴于同一点;③两直线交于x轴于同一点; ④方程2x-1 =0与4x-2=0的解相同; ⑤当x=1时,y1=y2=1. 其中正确的是 (填序号)
x=-3
(-3,0)
x=-2
③ ④
达标检测
4.已知关于的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标
是 .
(-2.0)
5.直线y=2x-1 和y=2x-2的位置关系为 ,因此可得方程组
的解的情况为_______.
6.二元一次方程组 的解即为一次函数 和 图象
的交点坐标.
平行
无解
y=2x-4
y=x-6
达标检测
7.旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购行李票,该行李费y(元),行李重量x(kg)的一次函数,如图所示.
求:⑴y与x之间的函数关系式;
⑵旅客最多可免费携带多少行李的重量.
y(元)
----------------
-------------
---------
-----
x(kg)
90
60
10
5
O
解:(1)设一次函数关系式为y=kx+b(k≠0)
把x=60,y=5和x=90,y=10代入得
5=60k+b
10=90k+b
(2)当y=0时,x=30
∴旅客最多可免费携带的行李重量是30kg 。
k=
b=-5
达标检测
∴一次函数的关系式为y=?????????????????(????≥????????)
?
1.二元一次方程与一次函数的关系
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上;
(2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
2.二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.
小结梳理
https://www.21cnjy.com/help/help_extract.php
八年级下册数学精品课件
17.5 实践与探索
学习目标
能根据一次函数的图象求二元一次方程组的解.
能通过数形结合说出一次函数与一元一次方程及一元一次不等式的联系.
会图象上获取信息的能力,利用数形结合解决实际问题.
问题1:学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙
复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.
两复印社每月收费情况如图所示.
根据图象回答:
(1)乙复印社的每月承包费是多少?
(2)当每月复印多少页时,两复印社实际
收费相同?
(3)如果每月复印页数在1200页左右,那么
应选择哪个复印社?
200元
800页
乙复印社
知识精讲
问题1:学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙
复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.
两复印社每月收费情况如图所示.
知识精讲
要点归纳:
由函数图象解答问题时,首先要明确横、纵轴表示的含义,函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定范围内,位于上方图象的函数值要比位于下方的图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确,观察得越仔细,所得的值就越准确.
知识精讲
2.谁出发的早?早多少时间?从哪可看出?
3.从哪可看出A车追上了B 车? 用了多少时间?
走了多少路程?
4.甲地到乙地的路程有多远?从哪可看出这一点?
1.图中的横坐标和纵坐标各表示什么含义?
·
(即当x取何值时,yA=yB ?)
知识精讲
问题2:下图中是A、B两车行驶的时间x(h)与行驶的路程y(km)的图象.
5.在4小时以前,哪车在前?
在4小时以后,哪车在前 ?
从图上怎么看?
6.你能从图上看出哪车的速度快?两条直线的倾斜程度表示了什么意义?
7.两车行驶的路程分别用yA、 yB表示, yA、 yB(km)与时间 x(h)之间的函数关系式分别是什么?
(即当x取何值时,yA>yB?)
(即当x取何值时,yA
y=10x
y=40x-120
8.若不解方程组,你能得到以下方程组的解吗?
9.若不解不等式 ,你能得到
以下不等式的解吗?
(1)10x>40x-120 (yA>yB)
(2)10x<40x-120( yA<yB)
知识精讲
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而两个一次函数的关系式就是方程组中的两个方程,所以交点的坐标就是方程组的解.
据此,我们可以利用图象来求某些方程组的解以及不等式的解集.
·
知识精讲
解:由x-2y=-2,可得y=12????+1
?
在同一直角坐标系内作出一次函数y=12????+1 的图象l1和y=2x-2的图象l2,如图所示
?
例1 用图象法解方程组
所以方程组?????2????=?22?????????=2 的解是????=2????=2
?
同理,由2x-y=2,可得y=2x-2
得l1,l2的交点为P(2,2).
典例解析
例2 利用图象解不等式:
(1)2x-5>-x+1, (2) 2x-5<-x+1.
解:设y1=2x-5,y2=-x+1,
在直角坐标系中画出这两条直线,如图.
两条直线的交点坐标是(2, -1) ,可知:
(1)2x--5>-x+1的解集是y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2.
典例解析
1.从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题的方法?
1) 图象法;2)数形结合法.
2.在观察图形时主要看图形中的哪几个关键地方?
1) 两坐标轴的含义;2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.
3.利用函数的图象我们刚才解决了哪几个问题?
1)求方程组的交点坐标;2)求不等式的解集.
总结提升
用图象法解二元一次方程组的具体方法:
1.先把两方程转化成y=kx+b 的形式;
2.在同一坐标系中画出两函数的图象;
3.找两函数的交点坐标,交点坐标即是方程组的解.
总结提升
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗?
(2)问43码的鞋相当于多少厘米的鞋?
x(厘米)
23
23.5
24.5
25.5
26
……
y(码)
36
37
39
41
42
……
针对练习
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画
出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
x (厘米)
y(码)
23
23.5
24
O
40
36
41
37
38
39
24.5
25.5
25
26
26.5
27
42
针对练习
解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得
所以y与x的函数关系式可能是:y=2x-10
(2)当y=43时,2x-10=43,
解得x=26.5.
针对练习
1.直线y=x+3与x轴的交点坐标为 ,所以相应的方程x+3=0的解是 .
2.设m,n为常数且m≠0,直线y=mx+n(如图所示),则方程mx+n=0的解是 .
3.对于y1=2x-1, y2=4x-2,下列说法:
①两直线平行; ②两直线交y轴于同一点;③两直线交于x轴于同一点; ④方程2x-1 =0与4x-2=0的解相同; ⑤当x=1时,y1=y2=1. 其中正确的是 (填序号)
x=-3
(-3,0)
x=-2
③ ④
达标检测
4.已知关于的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标
是 .
(-2.0)
5.直线y=2x-1 和y=2x-2的位置关系为 ,因此可得方程组
的解的情况为_______.
6.二元一次方程组 的解即为一次函数 和 图象
的交点坐标.
平行
无解
y=2x-4
y=x-6
达标检测
7.旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购行李票,该行李费y(元),行李重量x(kg)的一次函数,如图所示.
求:⑴y与x之间的函数关系式;
⑵旅客最多可免费携带多少行李的重量.
y(元)
----------------
-------------
---------
-----
x(kg)
90
60
10
5
O
解:(1)设一次函数关系式为y=kx+b(k≠0)
把x=60,y=5和x=90,y=10代入得
5=60k+b
10=90k+b
(2)当y=0时,x=30
∴旅客最多可免费携带的行李重量是30kg 。
k=
b=-5
达标检测
∴一次函数的关系式为y=?????????????????(????≥????????)
?
1.二元一次方程与一次函数的关系
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上;
(2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
2.二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.
小结梳理
https://www.21cnjy.com/help/help_extract.php
