椭圆的简单几何性质
图片预览






文档简介
课件54张PPT。复习:1.椭圆的定义:到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2当焦点在X轴上时当焦点在Y轴上时2.1.2《 椭圆的几何性质》2.2.2 椭圆的简单几何性质(1) 椭圆的几何性质
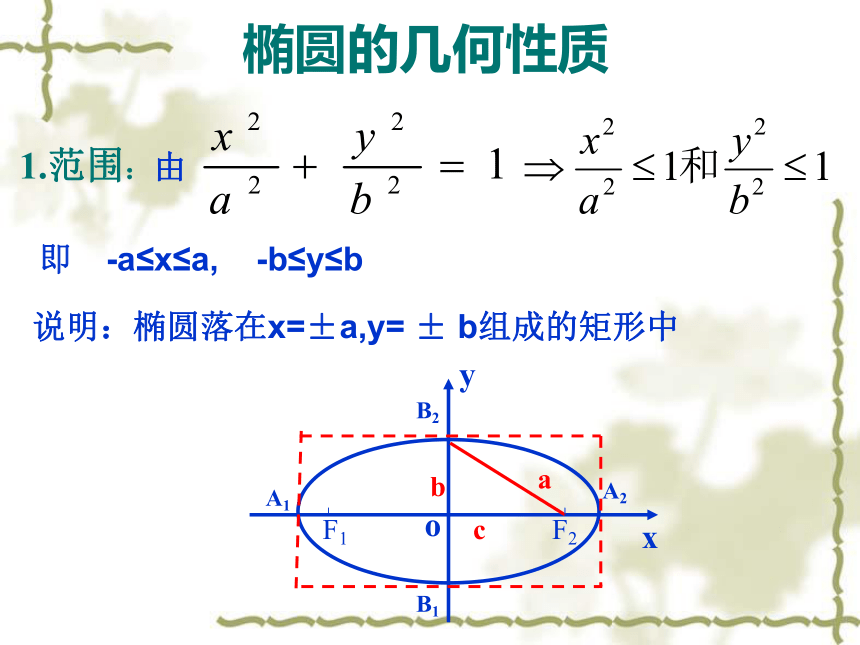
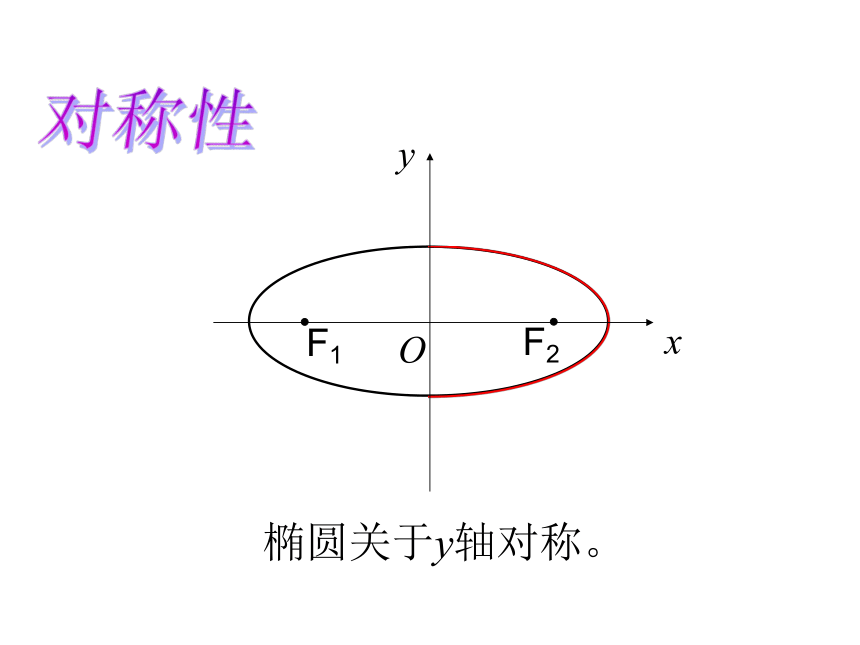
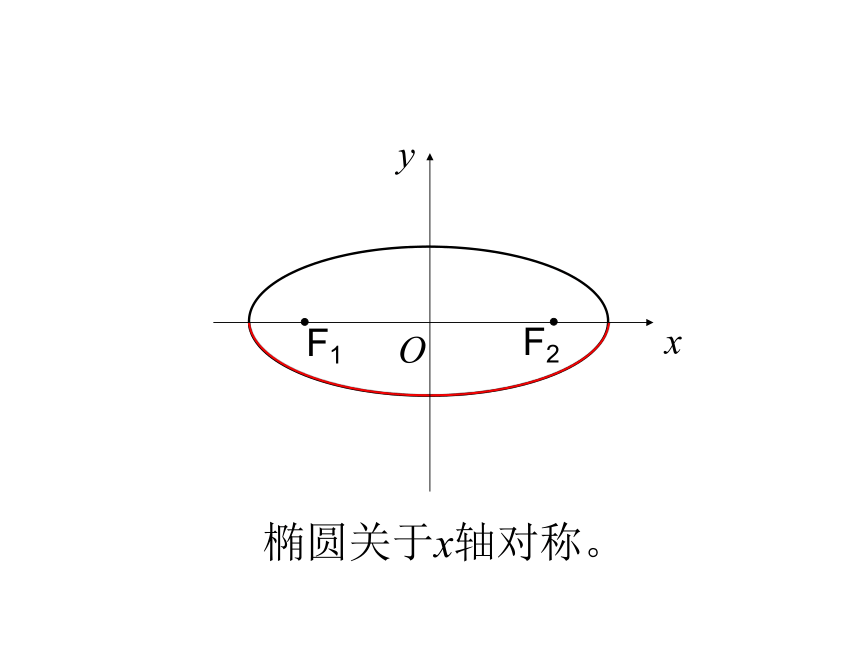
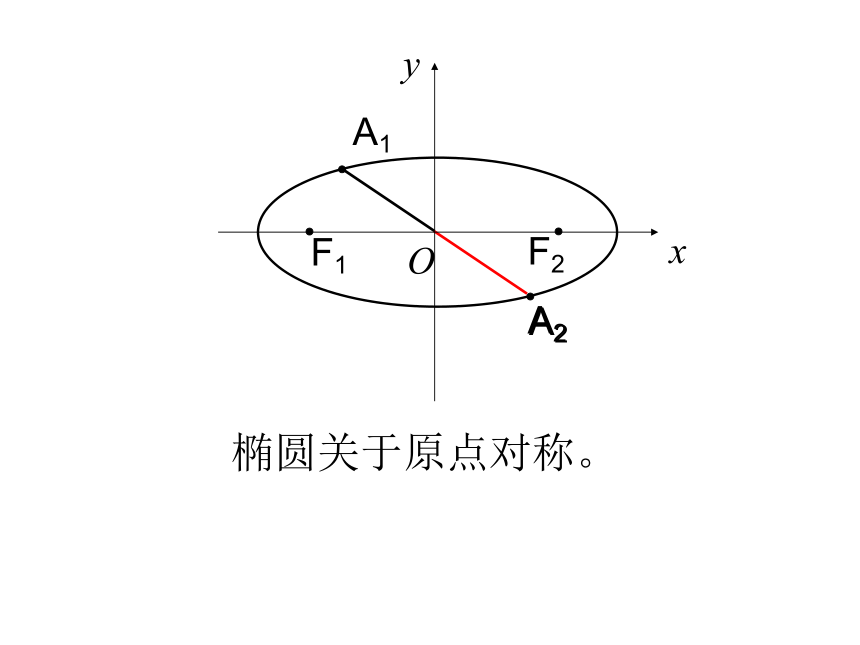
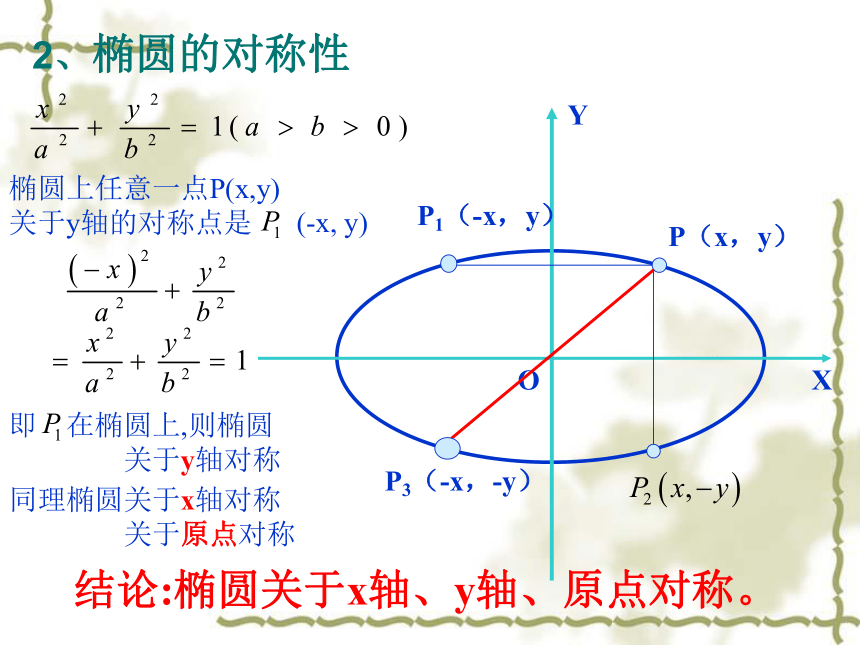
1.范围:由即 -a≤x≤a, -b≤y≤b说明:椭圆落在x=±a,y= ± b组成的矩形中x1.范 围:对称性F2F1Oxy椭圆关于y轴对称。F2F1Oxy椭圆关于x轴对称。A2A1F2F1Oxy椭圆关于原点对称。2、椭圆的对称性结论:椭圆关于x轴、y轴、原点对称。椭圆上任意一点P(x,y)
关于y轴的对称点是同理椭圆关于x轴对称
关于原点对称即 在椭圆上,则椭圆
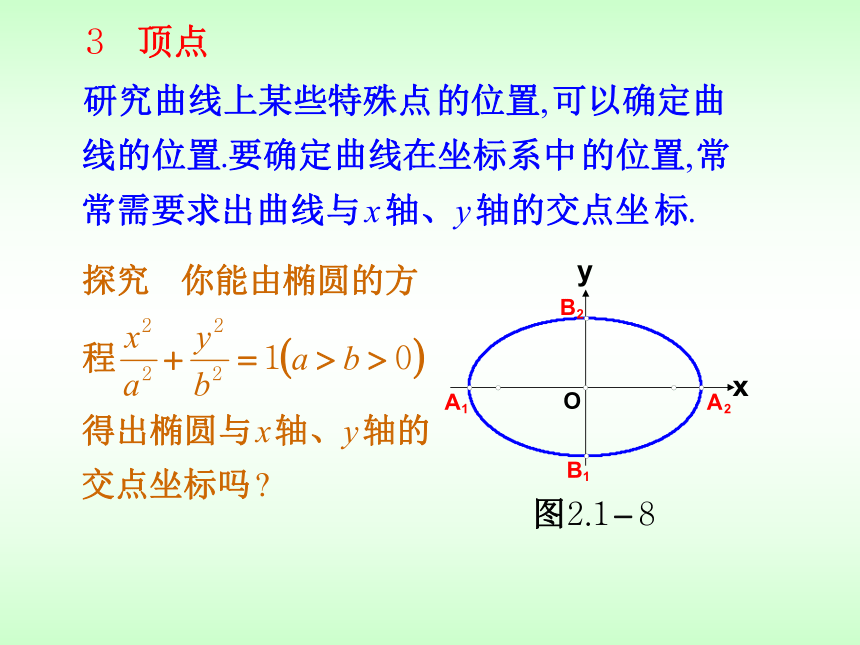
关于y轴对称(-x, y)3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。椭圆几何性质的应用
(1)椭圆的焦点决定椭圆的位置,范围决定椭圆的大小,离心率决定了椭圆的扁圆程度,对称性是椭圆的重要特征,顶点是椭圆与对称轴的交点,是椭圆重要的特殊点;若已知椭圆的标准方程,则根据a、b的值可确定其性质.
(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆的四个顶点,求焦点”的几何作图法,只要以短轴的端点B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就是焦点.
名师点睛1.学生活动(课本48页练习1)思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置? oB2B1A1A2F1F2因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.练习:课本48页24、离心率长半轴为 a
半焦距为 c思考:保持长半轴 a 不变,改变椭圆的半焦距 c ,我们可以发现,c 越接近 a ,椭圆越________
这样,我们就可以利用__和__这两个量来刻画椭圆的扁平程度
扁平ca看动画椭圆的离心率因为 a >c>0,所以 e 的取值范围是:_________02.练习:课本48页5(1)4、椭圆的离心率e与a,b的关系:|x|≤ a,|y|≤ b关于x 轴、y 轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ a,|y|≤ b关于x 轴、y 轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>b
a2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前椭圆的简单几何性质
自学导引(a>b>0)(a>b>0)-a≤x≤a且-b≤y≤b-b≤x≤b且-a≤y≤aA1(-a,0)、A2(a,0)B1(0,-b)、B2(0,b)A1(0,-a)、A2(0,a)B1(-b,0)、B2(b,0)2b2aF1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c)2cx轴和y轴(0,0)例4 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标因此,椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是解题的关键:1、将椭圆方程转化为标准方程
2、确定焦点的位置和长轴的位置例.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .解:(1)由椭圆的几何性质可知,点P、Q分别为椭圆长轴和短轴的一个端点.为所求椭圆的标准方程 .练习:课本48页4练习:课本48页3解:xy..FF ’O.M.例6.点M(x,y)与定点F(c,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹椭圆第二定义:xy..FF ’O.M活页规范训练4.已知椭圆的短轴长等于2,长轴端点与短轴端点间的距离等于 ,则此椭圆的标准方程是________.
解析 设椭圆的长半轴长为a,短半轴长为b,焦距为2c,
则b=1,a2+b2=( )2,即a2=4.
所以椭圆的标准方程是 +y2=1或 +x2=1.
答案 +y2=1或 +x2=15.已知椭圆 的离心率为 ,则k的值为________.
解析 当k+8>9时,e2= = = ,
k=4;
当k+8<9时,e2= = = ,
k=- .
答案 4或-7.已知椭圆x2+my2=1的焦点在y轴上,且长轴长是短轴长的2倍,则m= ( ).
A. B. C.2 D.4
解析 将椭圆方程化为标准方程为x2+ =1,
∵焦点在y轴上,
∴ >1,∴0由方程得a= ,b=1.∵a=2b,∴m= .
答案 A11.已知椭圆长轴长是短轴长的2倍,且过点A(2,-6).求椭圆的标准方程.
解 法一 依题意a=2b.
(1)当椭圆焦点在x轴上时,设椭圆方程为 .
代入点A(2,-6)坐标,得 ,解得b2=37,
∴a2=4b2=4×37=148,
∴椭圆的标准方程为 .
(2)当焦点在y轴上时,设椭圆方程为 .
代入点A(2,-6)坐标得 ,
∴b2=13,∴a2=52.
∴椭圆的标准方程为 .
综上所述,所求椭圆的标准方程为
或 .2.1.2《 椭圆的几何性质》2.2.2 椭圆的简单几何性质(2)自学导引直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法所以消y得一个一元二次方程
两一无>=<自学导引知识应用思考:最大距离为多少?例 .已知直线y=x- 与椭圆x2+4y2=2,判断它们的位置关系。解:联立方程组消去y?=36>0,因为所以方程(1)有两个根,变式1:交点坐标是什么?弦长公式:则原方程组有两组解.----- (1)知识应用所以该直线与椭圆相交.变式2:相交所得的弦的弦长是多少?
由韦达定理 k表示弦的斜率,x1、x2表示弦的端点坐标名师点睛 利用设而不解的方法求解直线与椭圆相交位置关系中的中点、弦长等问题是本节特别常见的方程思想方法.
方法技巧 函数方程思想在椭圆中的应用【示例】[思路分析] 求弦AB的长,需确定点A、B的坐标,点A、B是直线与椭圆的交点,因此由直线方程和椭圆方程组成方程组,解方程组,依据根与系数的关系和弦长公式可求解.
方法点评 解决直线与椭圆的位置关系问题经常利用设而不解的方法,解题步骤为:
(1)设直线与椭圆的交点为A(x1,y1),B(x2,y2);
(2)联立直线与椭圆的方程;
(3)消元得到关于x或y的一元二次方程;
(4)利用根与系数的关系设而不求;
(5)把题干中的条件转化为x1+x2,x1x2或y1+y2,y1y2,进而求解.
5.椭圆x2+4y2=16被直线y=x+1截得的弦长为________.
解析 由 消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
练习:课本48页7
关于y轴的对称点是同理椭圆关于x轴对称
关于原点对称即 在椭圆上,则椭圆
关于y轴对称(-x, y)3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。椭圆几何性质的应用
(1)椭圆的焦点决定椭圆的位置,范围决定椭圆的大小,离心率决定了椭圆的扁圆程度,对称性是椭圆的重要特征,顶点是椭圆与对称轴的交点,是椭圆重要的特殊点;若已知椭圆的标准方程,则根据a、b的值可确定其性质.
(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆的四个顶点,求焦点”的几何作图法,只要以短轴的端点B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就是焦点.
名师点睛1.学生活动(课本48页练习1)思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置? oB2B1A1A2F1F2因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.练习:课本48页24、离心率长半轴为 a
半焦距为 c思考:保持长半轴 a 不变,改变椭圆的半焦距 c ,我们可以发现,c 越接近 a ,椭圆越________
这样,我们就可以利用__和__这两个量来刻画椭圆的扁平程度
扁平ca看动画椭圆的离心率因为 a >c>0,所以 e 的取值范围是:_________0
a2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前椭圆的简单几何性质
自学导引(a>b>0)(a>b>0)-a≤x≤a且-b≤y≤b-b≤x≤b且-a≤y≤aA1(-a,0)、A2(a,0)B1(0,-b)、B2(0,b)A1(0,-a)、A2(0,a)B1(-b,0)、B2(b,0)2b2aF1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c)2cx轴和y轴(0,0)例4 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标因此,椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是解题的关键:1、将椭圆方程转化为标准方程
2、确定焦点的位置和长轴的位置例.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .解:(1)由椭圆的几何性质可知,点P、Q分别为椭圆长轴和短轴的一个端点.为所求椭圆的标准方程 .练习:课本48页4练习:课本48页3解:xy..FF ’O.M.例6.点M(x,y)与定点F(c,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹椭圆第二定义:xy..FF ’O.M活页规范训练4.已知椭圆的短轴长等于2,长轴端点与短轴端点间的距离等于 ,则此椭圆的标准方程是________.
解析 设椭圆的长半轴长为a,短半轴长为b,焦距为2c,
则b=1,a2+b2=( )2,即a2=4.
所以椭圆的标准方程是 +y2=1或 +x2=1.
答案 +y2=1或 +x2=15.已知椭圆 的离心率为 ,则k的值为________.
解析 当k+8>9时,e2= = = ,
k=4;
当k+8<9时,e2= = = ,
k=- .
答案 4或-7.已知椭圆x2+my2=1的焦点在y轴上,且长轴长是短轴长的2倍,则m= ( ).
A. B. C.2 D.4
解析 将椭圆方程化为标准方程为x2+ =1,
∵焦点在y轴上,
∴ >1,∴0
答案 A11.已知椭圆长轴长是短轴长的2倍,且过点A(2,-6).求椭圆的标准方程.
解 法一 依题意a=2b.
(1)当椭圆焦点在x轴上时,设椭圆方程为 .
代入点A(2,-6)坐标,得 ,解得b2=37,
∴a2=4b2=4×37=148,
∴椭圆的标准方程为 .
(2)当焦点在y轴上时,设椭圆方程为 .
代入点A(2,-6)坐标得 ,
∴b2=13,∴a2=52.
∴椭圆的标准方程为 .
综上所述,所求椭圆的标准方程为
或 .2.1.2《 椭圆的几何性质》2.2.2 椭圆的简单几何性质(2)自学导引直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法所以消y得一个一元二次方程
两一无>=<自学导引知识应用思考:最大距离为多少?例 .已知直线y=x- 与椭圆x2+4y2=2,判断它们的位置关系。解:联立方程组消去y?=36>0,因为所以方程(1)有两个根,变式1:交点坐标是什么?弦长公式:则原方程组有两组解.----- (1)知识应用所以该直线与椭圆相交.变式2:相交所得的弦的弦长是多少?
由韦达定理 k表示弦的斜率,x1、x2表示弦的端点坐标名师点睛 利用设而不解的方法求解直线与椭圆相交位置关系中的中点、弦长等问题是本节特别常见的方程思想方法.
方法技巧 函数方程思想在椭圆中的应用【示例】[思路分析] 求弦AB的长,需确定点A、B的坐标,点A、B是直线与椭圆的交点,因此由直线方程和椭圆方程组成方程组,解方程组,依据根与系数的关系和弦长公式可求解.
方法点评 解决直线与椭圆的位置关系问题经常利用设而不解的方法,解题步骤为:
(1)设直线与椭圆的交点为A(x1,y1),B(x2,y2);
(2)联立直线与椭圆的方程;
(3)消元得到关于x或y的一元二次方程;
(4)利用根与系数的关系设而不求;
(5)把题干中的条件转化为x1+x2,x1x2或y1+y2,y1y2,进而求解.
5.椭圆x2+4y2=16被直线y=x+1截得的弦长为________.
解析 由 消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
练习:课本48页7
