双曲线及其标准方程
图片预览





文档简介
课件41张PPT。双曲线及其标准方程
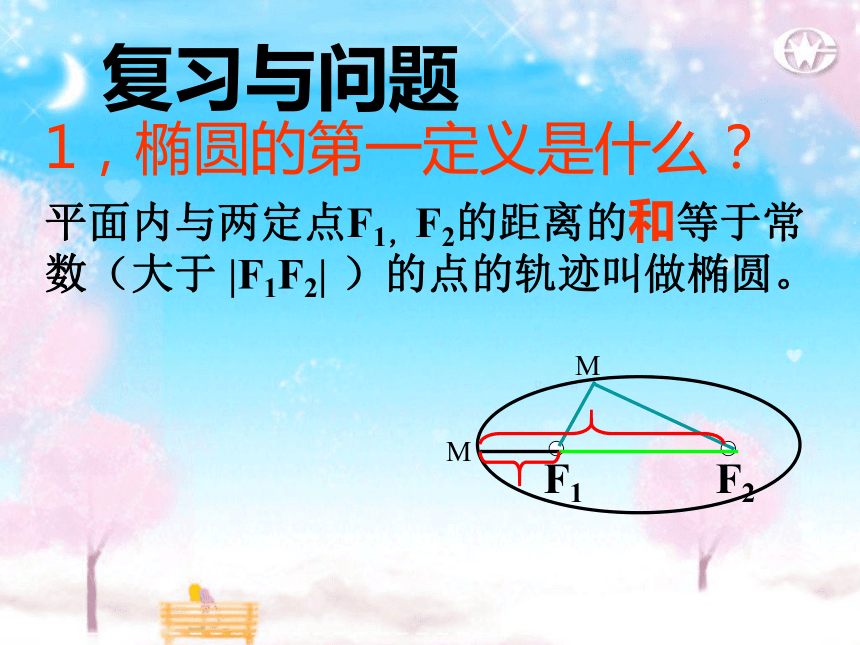
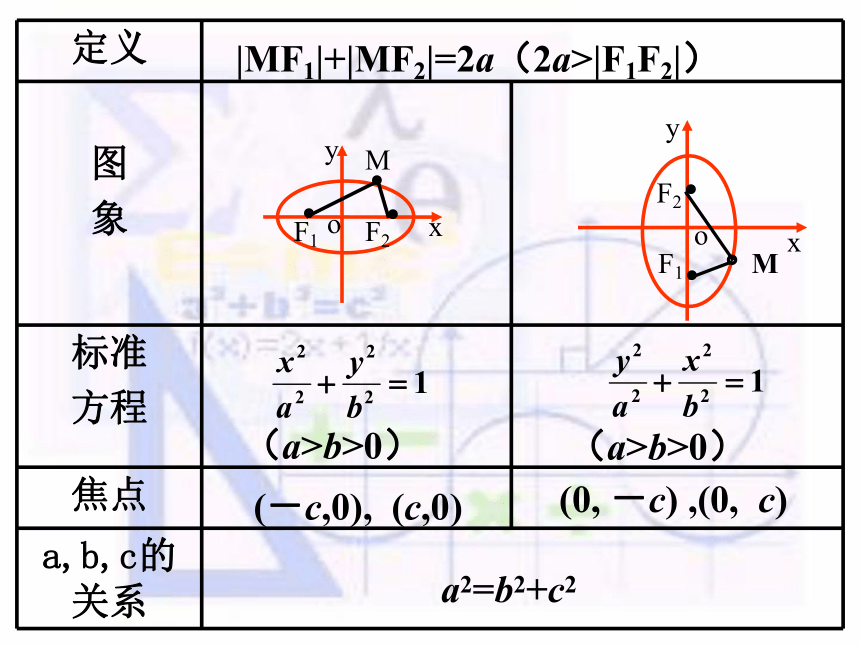
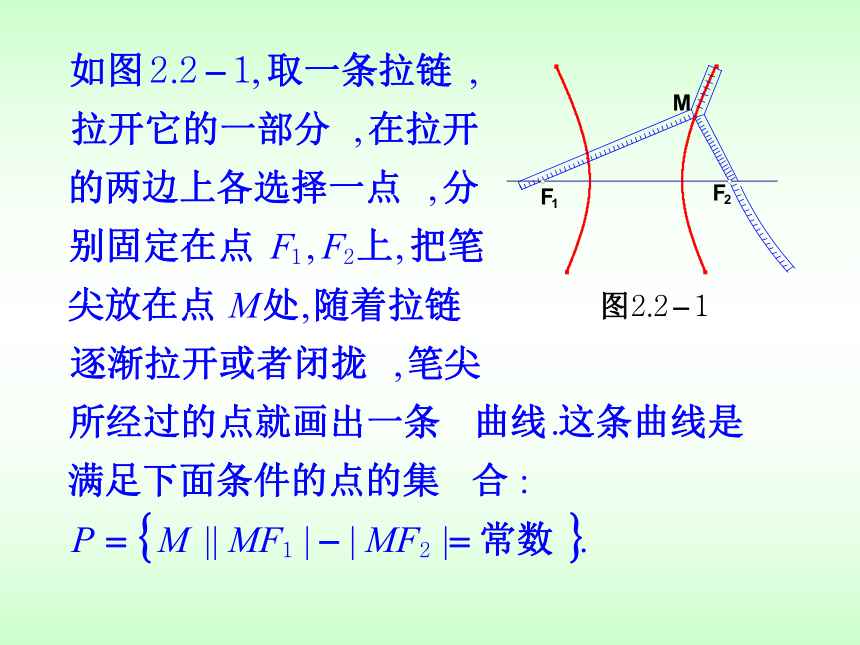
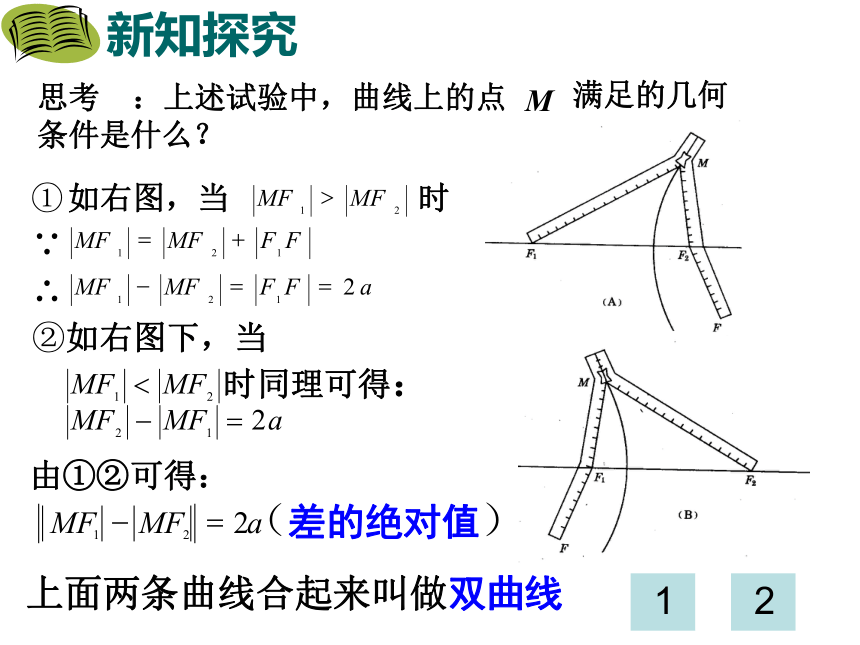
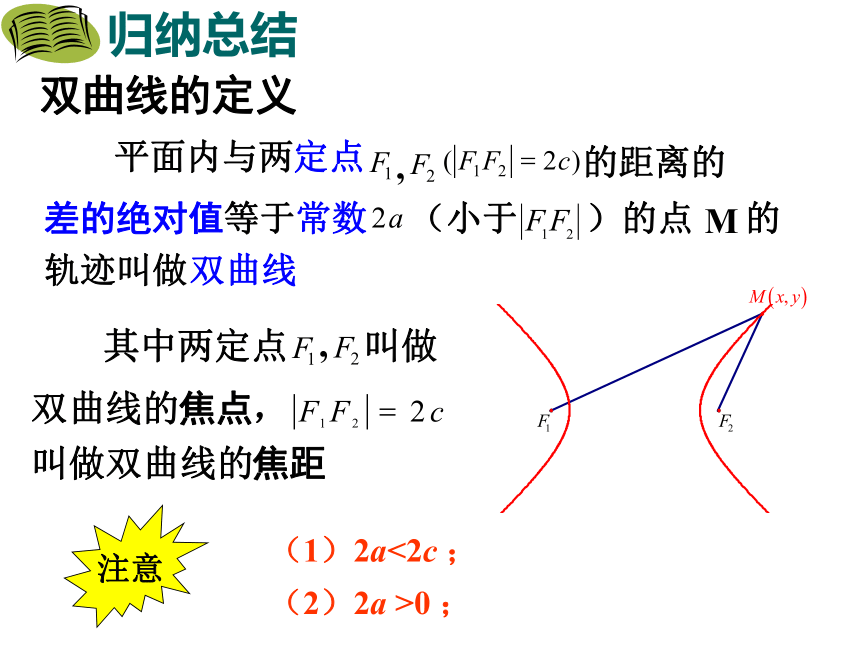
2.3.1 双曲线及其标准方程复习与问题1,椭圆的第一定义是什么?平面内与两定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆。F1F2M|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2 (-c,0), (c,0)(0, -c) ,(0, c)(a>b>0)(a>b>0)探究新知平面内M与两定点F1、F2的距离的差等于非零常数2a的点的轨迹是什么图形?思考:探求轨迹 平面内到两个定点F1、F2的距离的差等于常数的动点的轨迹又是怎样的?新知探究上面两条曲线合起来叫做双曲线思考:上述试验中,曲线上的点M满足的几何 条件是什么? 12归纳总结双曲线的定义(1)2a<2c ;(2)2a >0 ;注意 双曲线的定义
把平面内与两个定点F1、F2的距离的___________等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这_________叫做双曲线的焦点, _______________叫做双曲线的焦距.
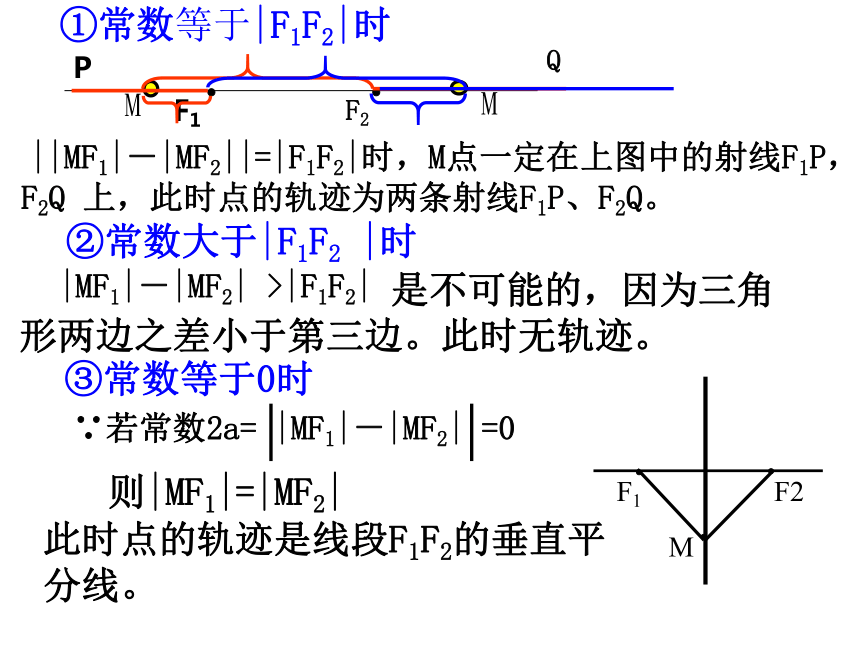
自学导引1.差的绝对值两个定点两焦点间的距离理解定义 ||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q 上,此时点的轨迹为两条射线F1P、F2Q。②常数大于|F1F2 |时①常数等于|F1F2|时PMQM 是不可能的,因为三角形两边之差小于第三边。此时无轨迹。此时点的轨迹是线段F1F2的垂直平分线。则|MF1|=|MF2|③常数等于0时提示 (1)若“常数等于|F1F2|”时,此时动点的轨迹是以F1,F2为端点的两条射线F1A,F2B(包括端点),如图所示.
(2)若“常数大于|F1F2|”,此时动点轨迹不存在.
(3)若“常数为0”,此时动点轨迹为线段F1F2的垂直平分线.
自学导引试说明在下列条件下动点M的轨迹各是什么图形?
(F1、F2是两定点, |F1F2| =2c (0 当|MF1|-|MF2|=2a时,点M的轨迹 ;
当|MF2|-|MF1|=2a时,点M的轨迹 ;
因此,在应用定义时,首先要考查 .双曲线的右支双曲线的左支以F1、F2为端点的两条射线不存在2a与2c的大小线段F1F2的垂直平分线F1F2若a=0,动点M的是轨迹_______________________. 若a=c,动点M的轨迹 ;
若a>c,动点M的轨迹 . 已知A(0,﹣4),B(0,4),
︱PA︱-︱PB︱=2a,当a=3和4时,点 p 轨迹分别为( )
A、双曲线和一条直线 B、双曲线和两条射线
C、双曲线一支和一条直线 D、双曲线一支和一条射
线D练一练:如何求双曲线的方程呢?oF1PF2以F1,F2所在的直线为X轴,线段F1F2的中垂线为 y轴建立直角坐标系,则F1(-C,0),F2(C,0)2C师生互动二、双曲线的标准方程设点列条件建系P(x,y)双曲线的标准方程:方程叫做双曲线的标准方程 它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2双曲线的标准方程 F1F2双曲线的标准方程:(a>0,b>0)方程叫做双曲线的标准方程 它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2x2y2方程叫做双曲线的标准方程它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2如果x2的系数是正时,那么焦点在x轴上P如果y2的系数是正时,那么焦点在y轴上双曲线的标准方程
2.a2+b2自学导引提示 如果x2项的系数是正的,那么焦点在x轴上,如果y2项的系数是正的,那么焦点在y轴上.对于双曲线,a不一定大于b,因此,不能像椭圆那样比较分母的大小来判定焦点在哪一个坐标轴上.
自学导引F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系:||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)已知方程 表示双曲线,则 的取值范围是____________.解:若此方程表示椭圆, 的取值范围?解:练一练:练一练:求下列双曲线的焦点坐标及a:y29-x216=1(1)(2) x2 - 3 y2 = 3课本 55页 练习 1课本 55页 练习 2课本 55页 练习 3例题分析解:由双曲线的定义知点 的轨迹是双曲线.因为双曲线的焦点在 轴上,所以设它的标准方程为所求双曲线的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.例题分析所求轨迹的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.两条射线轨迹不存在BA例2 一炮弹在某处爆炸,在 A处听到的时 间比在 B处晚2S,(1)爆炸点应在什么样的曲线上?(2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程.分析:解应用题的关键是建 立 根据本题题设和结论,注意到在A处听到爆炸声的时间比B处 ,这里声速取定值. 数学模型晚2s联系实际,数学建模 P解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点 更远,所以爆炸点应在靠近 处的一支上.
离A处比离B处 B四、联系实际,数学建模 (2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程..o (2)如图:建立直角坐标系,使A、B两点在轴 上,并且点O与线段AB的中点重合.又|AB|=800,∴2c=800,c=400, ∵|PA|-|PB|=680>0,所求双曲线的方程为:四、联系实际,数学建模 本题若|AB|=680m,曲线的方程是什么?A到B的距离恰好等于680米解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点离A处比离B处 更远,所以爆炸点应在靠近 B 处的一支上.解:(1) 若A、B两处距离差恰为2秒×声速,则爆炸点应在以B为端点的射线上.
故本题答案若为:爆炸点位于以A、B为焦点的双曲线靠近 B 处的一支上或在线段AB的延长线上,就更完美了。联系实际,
数学建模 A到B的距离恰好等于680米归纳应用:本例(2)利用两个不同的观测点得同一炮弹爆炸声的时间差,可以确定爆炸点所在的曲线的方程,但不能确定爆炸点的准确位置,如果再增设一个观测点C ,利用 A、C或(B、 C )两处测得的爆炸声的时间差,可以求出另一个曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.课本 54页 练习 5活页规范训练4.若双曲线8kx2-ky2=8的一个焦点坐标是(0,3),则实数k的值为________.
解析 因为双曲线焦点在y轴上,所以双曲线的标
准方程为 ,
所以k<0,又(0,3)是双曲线的一个焦点,
则c=3,于是有 ,解得k=-1.
答案 -15.已知P是双曲线 上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
解析 由双曲线方程 知,
a=8,b=6,则c .
∵P是双曲线上一点,
∴||PF1|-|PF2||=2a=16,
又|PF1|=17,
∴|PF2|=1或|PF2|=33.
又|PF2|≥c-a=2,
∴|PF2|=33.
答案 336.(2)已知双曲线与椭圆 有共同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求双曲线的方程.
解 (2)因为椭圆 的焦点为(0,-3),(0,3),A点的坐标为(± ,4),
设双曲线的标准方程为 (a>0,b>0),
所以 解得
所以所求的双曲线的标准方程为 .9.双曲线 的一个焦点到中心的距离
为3,那么m=________.
解析 (1)当焦点在x轴上,有m>5,
则c2=m+m-5=9,
∴m=7;
(2)当焦点在y轴上,有m<0,
则c2=-m+5-m=9,
∴m=-2;
综上述,m=7或m=-2.
答案 7或-210.已知椭圆 与双曲线
有相同的焦点,则实数a=________.
解析 由双曲线 可知a>0,且焦点在x轴上.
根据题意知4-a2=a+2,即a2+a-2=0,
解得a=1或a=-2(舍去),
故实数a=1.
答案 1
2.3.1 双曲线及其标准方程复习与问题1,椭圆的第一定义是什么?平面内与两定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆。F1F2M|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2 (-c,0), (c,0)(0, -c) ,(0, c)(a>b>0)(a>b>0)探究新知平面内M与两定点F1、F2的距离的差等于非零常数2a的点的轨迹是什么图形?思考:探求轨迹 平面内到两个定点F1、F2的距离的差等于常数的动点的轨迹又是怎样的?新知探究上面两条曲线合起来叫做双曲线思考:上述试验中,曲线上的点M满足的几何 条件是什么? 12归纳总结双曲线的定义(1)2a<2c ;(2)2a >0 ;注意 双曲线的定义
把平面内与两个定点F1、F2的距离的___________等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这_________叫做双曲线的焦点, _______________叫做双曲线的焦距.
自学导引1.差的绝对值两个定点两焦点间的距离理解定义 ||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q 上,此时点的轨迹为两条射线F1P、F2Q。②常数大于|F1F2 |时①常数等于|F1F2|时PMQM 是不可能的,因为三角形两边之差小于第三边。此时无轨迹。此时点的轨迹是线段F1F2的垂直平分线。则|MF1|=|MF2|③常数等于0时提示 (1)若“常数等于|F1F2|”时,此时动点的轨迹是以F1,F2为端点的两条射线F1A,F2B(包括端点),如图所示.
(2)若“常数大于|F1F2|”,此时动点轨迹不存在.
(3)若“常数为0”,此时动点轨迹为线段F1F2的垂直平分线.
自学导引试说明在下列条件下动点M的轨迹各是什么图形?
(F1、F2是两定点, |F1F2| =2c (0
当|MF2|-|MF1|=2a时,点M的轨迹 ;
因此,在应用定义时,首先要考查 .双曲线的右支双曲线的左支以F1、F2为端点的两条射线不存在2a与2c的大小线段F1F2的垂直平分线F1F2若a=0,动点M的是轨迹_______________________. 若a=c,动点M的轨迹 ;
若a>c,动点M的轨迹 . 已知A(0,﹣4),B(0,4),
︱PA︱-︱PB︱=2a,当a=3和4时,点 p 轨迹分别为( )
A、双曲线和一条直线 B、双曲线和两条射线
C、双曲线一支和一条直线 D、双曲线一支和一条射
线D练一练:如何求双曲线的方程呢?oF1PF2以F1,F2所在的直线为X轴,线段F1F2的中垂线为 y轴建立直角坐标系,则F1(-C,0),F2(C,0)2C师生互动二、双曲线的标准方程设点列条件建系P(x,y)双曲线的标准方程:方程叫做双曲线的标准方程 它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2双曲线的标准方程 F1F2双曲线的标准方程:(a>0,b>0)方程叫做双曲线的标准方程 它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2x2y2方程叫做双曲线的标准方程它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2如果x2的系数是正时,那么焦点在x轴上P如果y2的系数是正时,那么焦点在y轴上双曲线的标准方程
2.a2+b2自学导引提示 如果x2项的系数是正的,那么焦点在x轴上,如果y2项的系数是正的,那么焦点在y轴上.对于双曲线,a不一定大于b,因此,不能像椭圆那样比较分母的大小来判定焦点在哪一个坐标轴上.
自学导引F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系:||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)已知方程 表示双曲线,则 的取值范围是____________.解:若此方程表示椭圆, 的取值范围?解:练一练:练一练:求下列双曲线的焦点坐标及a:y29-x216=1(1)(2) x2 - 3 y2 = 3课本 55页 练习 1课本 55页 练习 2课本 55页 练习 3例题分析解:由双曲线的定义知点 的轨迹是双曲线.因为双曲线的焦点在 轴上,所以设它的标准方程为所求双曲线的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.例题分析所求轨迹的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.两条射线轨迹不存在BA例2 一炮弹在某处爆炸,在 A处听到的时 间比在 B处晚2S,(1)爆炸点应在什么样的曲线上?(2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程.分析:解应用题的关键是建 立 根据本题题设和结论,注意到在A处听到爆炸声的时间比B处 ,这里声速取定值. 数学模型晚2s联系实际,数学建模 P解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点 更远,所以爆炸点应在靠近 处的一支上.
离A处比离B处 B四、联系实际,数学建模 (2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程..o (2)如图:建立直角坐标系,使A、B两点在轴 上,并且点O与线段AB的中点重合.又|AB|=800,∴2c=800,c=400, ∵|PA|-|PB|=680>0,所求双曲线的方程为:四、联系实际,数学建模 本题若|AB|=680m,曲线的方程是什么?A到B的距离恰好等于680米解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点离A处比离B处 更远,所以爆炸点应在靠近 B 处的一支上.解:(1) 若A、B两处距离差恰为2秒×声速,则爆炸点应在以B为端点的射线上.
故本题答案若为:爆炸点位于以A、B为焦点的双曲线靠近 B 处的一支上或在线段AB的延长线上,就更完美了。联系实际,
数学建模 A到B的距离恰好等于680米归纳应用:本例(2)利用两个不同的观测点得同一炮弹爆炸声的时间差,可以确定爆炸点所在的曲线的方程,但不能确定爆炸点的准确位置,如果再增设一个观测点C ,利用 A、C或(B、 C )两处测得的爆炸声的时间差,可以求出另一个曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.课本 54页 练习 5活页规范训练4.若双曲线8kx2-ky2=8的一个焦点坐标是(0,3),则实数k的值为________.
解析 因为双曲线焦点在y轴上,所以双曲线的标
准方程为 ,
所以k<0,又(0,3)是双曲线的一个焦点,
则c=3,于是有 ,解得k=-1.
答案 -15.已知P是双曲线 上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
解析 由双曲线方程 知,
a=8,b=6,则c .
∵P是双曲线上一点,
∴||PF1|-|PF2||=2a=16,
又|PF1|=17,
∴|PF2|=1或|PF2|=33.
又|PF2|≥c-a=2,
∴|PF2|=33.
答案 336.(2)已知双曲线与椭圆 有共同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求双曲线的方程.
解 (2)因为椭圆 的焦点为(0,-3),(0,3),A点的坐标为(± ,4),
设双曲线的标准方程为 (a>0,b>0),
所以 解得
所以所求的双曲线的标准方程为 .9.双曲线 的一个焦点到中心的距离
为3,那么m=________.
解析 (1)当焦点在x轴上,有m>5,
则c2=m+m-5=9,
∴m=7;
(2)当焦点在y轴上,有m<0,
则c2=-m+5-m=9,
∴m=-2;
综上述,m=7或m=-2.
答案 7或-210.已知椭圆 与双曲线
有相同的焦点,则实数a=________.
解析 由双曲线 可知a>0,且焦点在x轴上.
根据题意知4-a2=a+2,即a2+a-2=0,
解得a=1或a=-2(舍去),
故实数a=1.
答案 1
