北师大版七年级数学下册 4.1 认识三角形 课件 (共19张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.1 认识三角形 课件 (共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 16:56:17 | ||
图片预览





文档简介
(共19张PPT)
4.1.2 认识三角形
第四章 三角形
北师大版七年级数学下册
检查预习情况
学生小组内统一预习自测答案,
并派代表展示本组答案
渔夫能叉到对岸的鱼吗?
有一个渔夫身高1.7米,河宽4米,他的手里有一把长为2米的鱼叉,他能叉到对岸漂起来的鱼吗?
学习目标
1、认识等腰三角形,会将三角形按边进行分 类;
2、掌握三角形三条边之间的关系;
3、能熟练应用三角形的三边关系解决问题;
重点:三角形的三边关系;
难点:应用三角形三边关系解决实际问题。
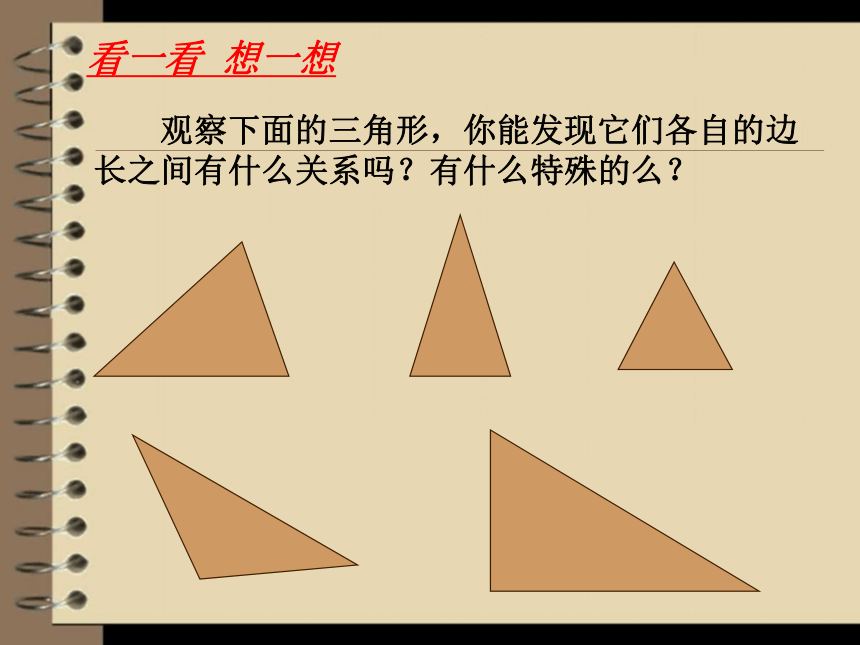
看一看 想一想
观察下面的三角形,你能发现它们各自的边长之间有什么关系吗?有什么特殊的么?
顶角
腰
腰
底角
底角
底边
探究一:三角形按边分类
1、不等边三角形(三边都不相等)
2、等腰三角形(两边相等)
3、等边三角形(三边都相等,也叫正三角形)
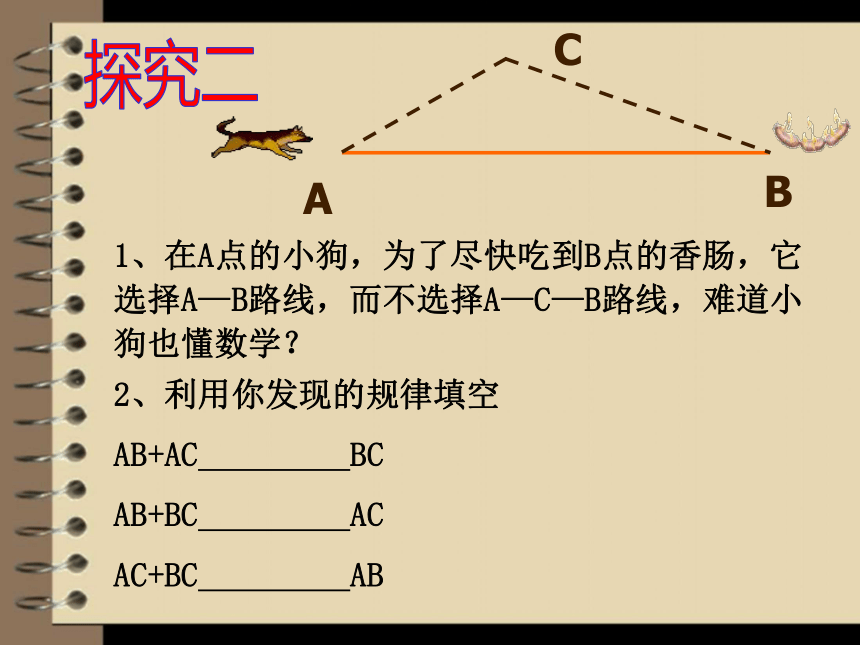
1、在A点的小狗,为了尽快吃到B点的香肠,它选择A—B路线,而不选择A—C—B路线,难道小狗也懂数学?
C
B
A
2、利用你发现的规律填空
AB+AC BC
AB+BC AC
AC+BC AB
3、在一个三角形中,任意两边之和与第三边的长度有怎样的关系 为什么 由此你能得到什么结论
三角形任意两边之和大于第三边
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论?
a-b____c; b-c____a; c-a____b
选择一个三角形量出三边长度,并填入空格内。
a
c
b
a
c
b
a
b
c
a = ,
b = ,
c = 。
a = ,
b = ,
c = 。
a = ,
b = ,
c = 。
分组合作
三角形三边关系
三角形任意两边之差小于第三边
三角形任意两边之和大于第三边
[例1]有两根长度分别为4cm和9cm的木棒,用长度为3cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?第三边的取值范围是什么?
三角形第三边的取值范围是:
两边之差<第三边<两边之和
应用探究
2、若设a,b,c 是是三角形的三边长,则
1、三角形两边是长分别是a、b,求第三边长c的取值范围是( )。
拓展提升
【例2】某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一个点P,使得点P到ABCD四点的距离之和最小吗 请说明理由。
A
B
C
D
P
P1
应用探究
课堂小结
本节课你有那些收获?谈谈你的感受。
你还有无疑问?
当堂检测
完成学案中的当堂检测部分
作业
必做题:课堂精炼120页训练案
选做题:121页加强案
谢谢
4.1.2 认识三角形
第四章 三角形
北师大版七年级数学下册
检查预习情况
学生小组内统一预习自测答案,
并派代表展示本组答案
渔夫能叉到对岸的鱼吗?
有一个渔夫身高1.7米,河宽4米,他的手里有一把长为2米的鱼叉,他能叉到对岸漂起来的鱼吗?
学习目标
1、认识等腰三角形,会将三角形按边进行分 类;
2、掌握三角形三条边之间的关系;
3、能熟练应用三角形的三边关系解决问题;
重点:三角形的三边关系;
难点:应用三角形三边关系解决实际问题。
看一看 想一想
观察下面的三角形,你能发现它们各自的边长之间有什么关系吗?有什么特殊的么?
顶角
腰
腰
底角
底角
底边
探究一:三角形按边分类
1、不等边三角形(三边都不相等)
2、等腰三角形(两边相等)
3、等边三角形(三边都相等,也叫正三角形)
1、在A点的小狗,为了尽快吃到B点的香肠,它选择A—B路线,而不选择A—C—B路线,难道小狗也懂数学?
C
B
A
2、利用你发现的规律填空
AB+AC BC
AB+BC AC
AC+BC AB
3、在一个三角形中,任意两边之和与第三边的长度有怎样的关系 为什么 由此你能得到什么结论
三角形任意两边之和大于第三边
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论?
a-b____c; b-c____a; c-a____b
选择一个三角形量出三边长度,并填入空格内。
a
c
b
a
c
b
a
b
c
a = ,
b = ,
c = 。
a = ,
b = ,
c = 。
a = ,
b = ,
c = 。
分组合作
三角形三边关系
三角形任意两边之差小于第三边
三角形任意两边之和大于第三边
[例1]有两根长度分别为4cm和9cm的木棒,用长度为3cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?第三边的取值范围是什么?
三角形第三边的取值范围是:
两边之差<第三边<两边之和
应用探究
2、若设a,b,c 是是三角形的三边长,则
1、三角形两边是长分别是a、b,求第三边长c的取值范围是( )。
拓展提升
【例2】某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一个点P,使得点P到ABCD四点的距离之和最小吗 请说明理由。
A
B
C
D
P
P1
应用探究
课堂小结
本节课你有那些收获?谈谈你的感受。
你还有无疑问?
当堂检测
完成学案中的当堂检测部分
作业
必做题:课堂精炼120页训练案
选做题:121页加强案
谢谢
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
