8.1 基本立体图形 第一课时 棱柱、棱锥、棱台的结构特征同步练习(word含解析)
文档属性
| 名称 | 8.1 基本立体图形 第一课时 棱柱、棱锥、棱台的结构特征同步练习(word含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览

文档简介
8.1 基本立体图形 第一课时 棱柱、棱锥、棱台的结构特征同步练习
一、选择题
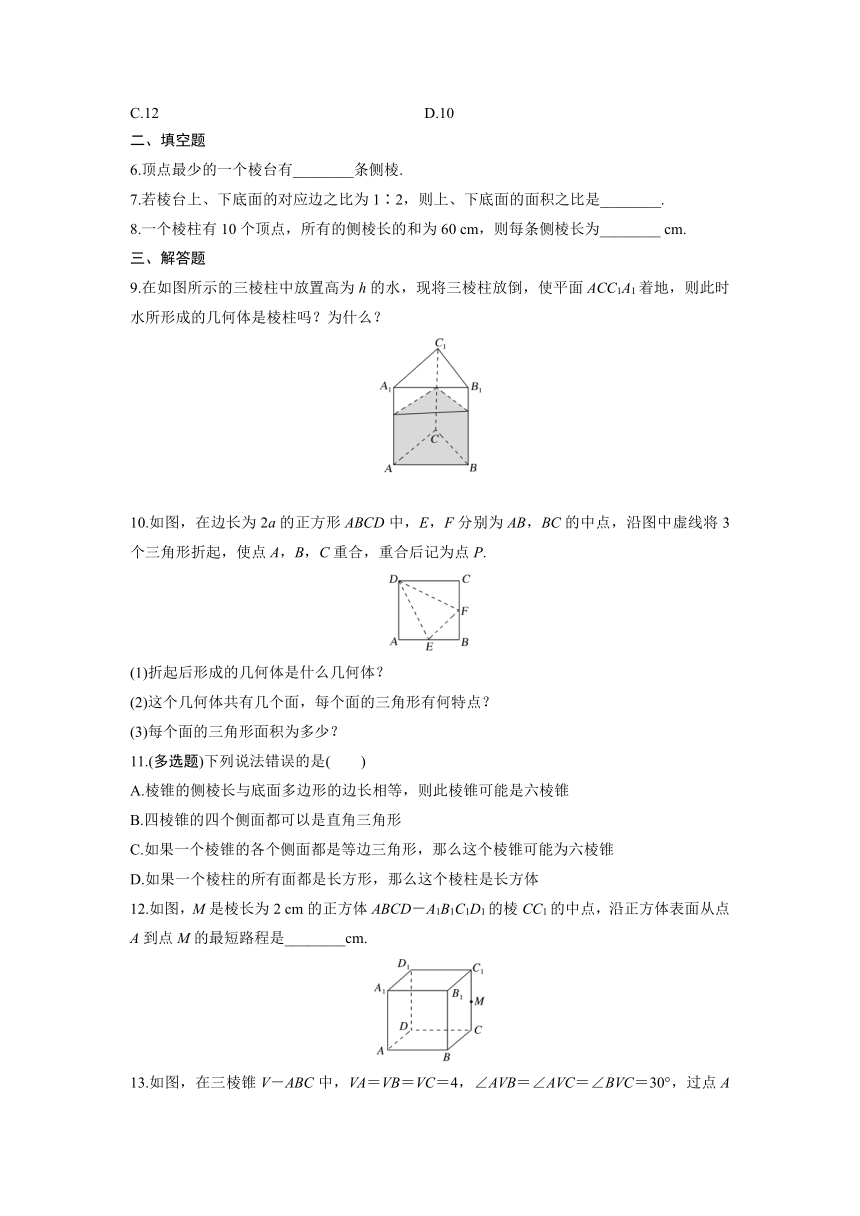
1.下列特征不是棱台必须具有的是( )
A.两底面平行 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后相交于一点
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
4.下列说法中正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
5.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15
C.12 D.10
二、填空题
6.顶点最少的一个棱台有________条侧棱.
7.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
8.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为________ cm.
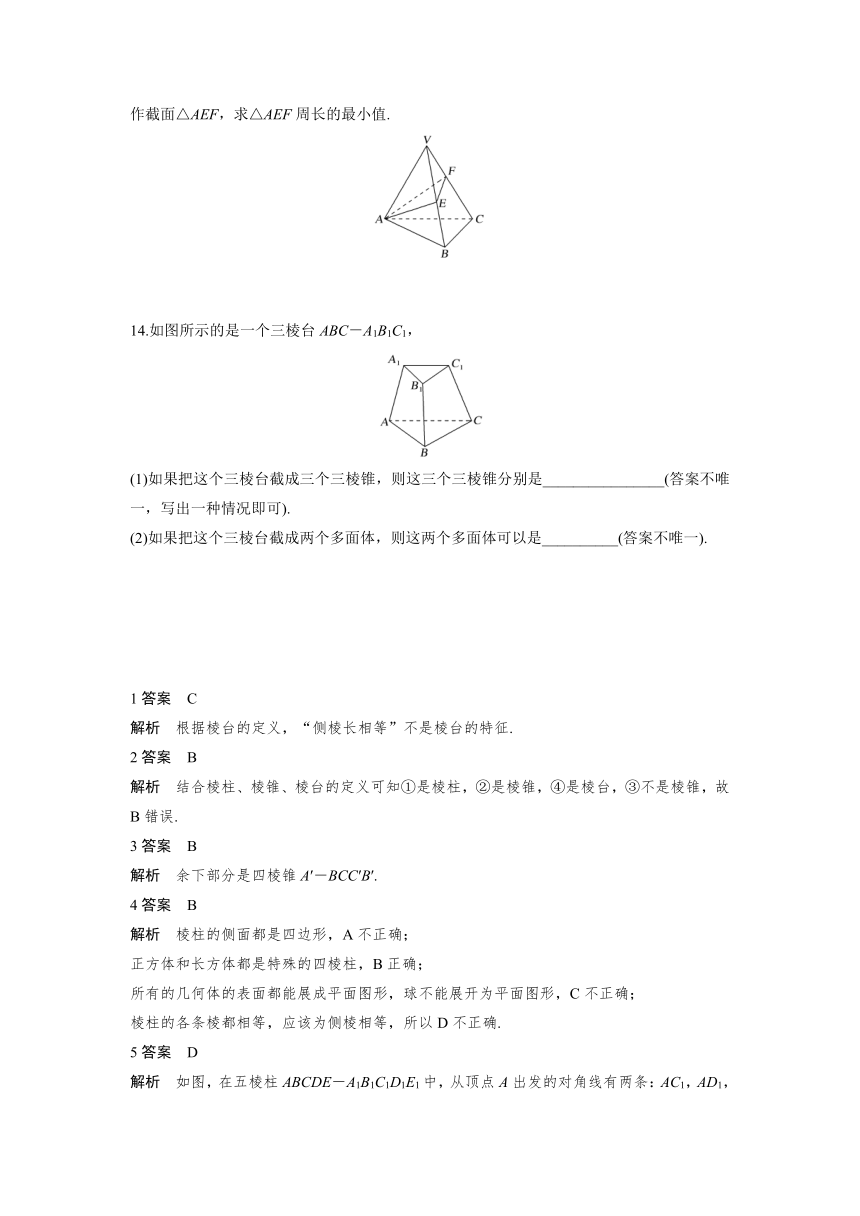
三、解答题
9.在如图所示的三棱柱中放置高为h的水,现将三棱柱放倒,使平面ACC1A1着地,则此时水所形成的几何体是棱柱吗?为什么?
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
11.(多选题)下列说法错误的是( )
A.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
B.四棱锥的四个侧面都可以是直角三角形
C.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体
12.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
13.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
14.如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________(答案不唯一,写出一种情况即可).
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(答案不唯一).
1答案 C
解析 根据棱台的定义,“侧棱长相等”不是棱台的特征.
2答案 B
解析 结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.
3答案 B
解析 余下部分是四棱锥A′-BCC′B′.
4答案 B
解析 棱柱的侧面都是四边形,A不正确;
正方体和长方体都是特殊的四棱柱,B正确;
所有的几何体的表面都能展成平面图形,球不能展开为平面图形,C不正确;
棱柱的各条棱都相等,应该为侧棱相等,所以D不正确.
5答案 D
解析 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共2×5=10(条).
6答案 3
解析 顶点最少的棱台是三棱台,有3条侧棱.
7答案 1∶4
解析 由棱台的结构特征知,棱台上、下底面是相似多边形,面积之比为对应边之比的平方.
8答案 12
解析 因棱柱有10个顶点,所以该棱柱为五棱柱,共有五条侧棱,所以侧棱长为=12(cm).
9解 是棱柱.如图所示,这是因为将平面ACC1A1着地,上面的水平面为DD1E1E,则水所形成的几何体为四棱柱ADEC-A1D1E1C1.
其中面ADEC与面A1D1E1C1平行且全等,侧面AA1D1D,DD1E1E,CC1E1E,AA1C1C分别为平行四边形,故水所形成的几何体为棱柱.
10解 (1)如图,折起后的几何体是三棱锥.
(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.
(3)S△PEF=a2,
S△DPF=S△DPE=×2a×a=a2,
S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE
=(2a)2-a2-a2-a2=a2.
11答案 AC
解析 对于A,若六棱锥的所有棱长都相等,则底面多边形是正六边形,若以正六边形为底面,侧棱长必然要大于底面边长,故A错误;对于B,四棱锥的四个侧面都可以是直角三角形,如图所示,故B正确;选项C,当棱锥的各个侧面的共顶点的角之和是360°时,各侧面构成平面图形,故这个棱锥不可能为六棱锥,故C错误;选项D,若每个侧面都是长方形,则说明侧棱与底面垂直,又底面也是长方形,符合长方体的定义,故D正确.
12答案
解析 由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1 cm,4 cm,故两点之间的距离是 cm.故沿正方体表面从点A到点M的最短路程是 cm.
13解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.
∴△AEF周长的最小值为4.
14答案 (1)A1-ABC,A1-BB1C1,A1-BCC1(答案不唯一) (2)两个三棱台(答案不唯一,也可以是一个三棱柱和一个五面体或一个三棱锥和一个五面体)
解析 (1)如图①所示,所截成的三个三棱锥分别是A1-ABC,A1-BB1C1,A1-BCC1.
(2)用平行于三棱台的底面的平面去截,可以得到两个三棱台,也可以截成一个三棱柱和一个五面体,如图②所示,也可以截成一个三棱锥和一个五面体,如图③所示.
图①
图② 图③
一、选择题
1.下列特征不是棱台必须具有的是( )
A.两底面平行 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后相交于一点
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
4.下列说法中正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
5.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15
C.12 D.10
二、填空题
6.顶点最少的一个棱台有________条侧棱.
7.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
8.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为________ cm.
三、解答题
9.在如图所示的三棱柱中放置高为h的水,现将三棱柱放倒,使平面ACC1A1着地,则此时水所形成的几何体是棱柱吗?为什么?
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
11.(多选题)下列说法错误的是( )
A.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
B.四棱锥的四个侧面都可以是直角三角形
C.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体
12.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
13.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
14.如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________(答案不唯一,写出一种情况即可).
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(答案不唯一).
1答案 C
解析 根据棱台的定义,“侧棱长相等”不是棱台的特征.
2答案 B
解析 结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.
3答案 B
解析 余下部分是四棱锥A′-BCC′B′.
4答案 B
解析 棱柱的侧面都是四边形,A不正确;
正方体和长方体都是特殊的四棱柱,B正确;
所有的几何体的表面都能展成平面图形,球不能展开为平面图形,C不正确;
棱柱的各条棱都相等,应该为侧棱相等,所以D不正确.
5答案 D
解析 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共2×5=10(条).
6答案 3
解析 顶点最少的棱台是三棱台,有3条侧棱.
7答案 1∶4
解析 由棱台的结构特征知,棱台上、下底面是相似多边形,面积之比为对应边之比的平方.
8答案 12
解析 因棱柱有10个顶点,所以该棱柱为五棱柱,共有五条侧棱,所以侧棱长为=12(cm).
9解 是棱柱.如图所示,这是因为将平面ACC1A1着地,上面的水平面为DD1E1E,则水所形成的几何体为四棱柱ADEC-A1D1E1C1.
其中面ADEC与面A1D1E1C1平行且全等,侧面AA1D1D,DD1E1E,CC1E1E,AA1C1C分别为平行四边形,故水所形成的几何体为棱柱.
10解 (1)如图,折起后的几何体是三棱锥.
(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.
(3)S△PEF=a2,
S△DPF=S△DPE=×2a×a=a2,
S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE
=(2a)2-a2-a2-a2=a2.
11答案 AC
解析 对于A,若六棱锥的所有棱长都相等,则底面多边形是正六边形,若以正六边形为底面,侧棱长必然要大于底面边长,故A错误;对于B,四棱锥的四个侧面都可以是直角三角形,如图所示,故B正确;选项C,当棱锥的各个侧面的共顶点的角之和是360°时,各侧面构成平面图形,故这个棱锥不可能为六棱锥,故C错误;选项D,若每个侧面都是长方形,则说明侧棱与底面垂直,又底面也是长方形,符合长方体的定义,故D正确.
12答案
解析 由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1 cm,4 cm,故两点之间的距离是 cm.故沿正方体表面从点A到点M的最短路程是 cm.
13解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.
∴△AEF周长的最小值为4.
14答案 (1)A1-ABC,A1-BB1C1,A1-BCC1(答案不唯一) (2)两个三棱台(答案不唯一,也可以是一个三棱柱和一个五面体或一个三棱锥和一个五面体)
解析 (1)如图①所示,所截成的三个三棱锥分别是A1-ABC,A1-BB1C1,A1-BCC1.
(2)用平行于三棱台的底面的平面去截,可以得到两个三棱台,也可以截成一个三棱柱和一个五面体,如图②所示,也可以截成一个三棱锥和一个五面体,如图③所示.
图①
图② 图③
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
