4.2图形的全等 课时练习

4.2图形的全等
一、单选题
1.下列说法正确的是（　　）
A. 所有的等边三角形都是全等三角形 B. 全等三角形是指面积相等的三角形
C. 周长相等的三角形是全等三角形 D. 全等三角形是指形状相同大小相等的三角形
2.下列说法中，错误的是（　　）
A. 全等三角形对应角相等 B. 全等三角形对应边相等
C. 全等三角形的面积相等 D. 面积相等的两个三角形一定全等
3.下列命题①两个图形全等，它们的形状相同；②两个图形全等，它们的大小相同；③面积相等的两个图形全等；④周长相等的两个图形全等．其中正确的个数为（ ）
A.1个
B.2个
C.3个
D.4个
4.全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC和△A1B1C1是全等（合同）三角形，点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形 如图，若运动方向相反，则称它们是镜面合同三角形 如图，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，两个镜面合同三角形要重合，则必须将其中一个翻转180° 如图，下列各组合同三角形中，是镜面合同三角形的是（　　）
A. B. C. D.
5.下列说法正确的是（　　）
A. 全等三角形是指形状相同的三角形 B. 全等三角形是指面积相等的两个三角形
C. 全等三角形的周长和面积相等 D. 所有等边三角形是全等三角形
6.下列说法正确的是（　　）
A. 形状相同的两个三角形全等 B. 面积相等的两个三角形全等
C. 完全重合的两个三角形全等 D. 所有的等边三角形全等
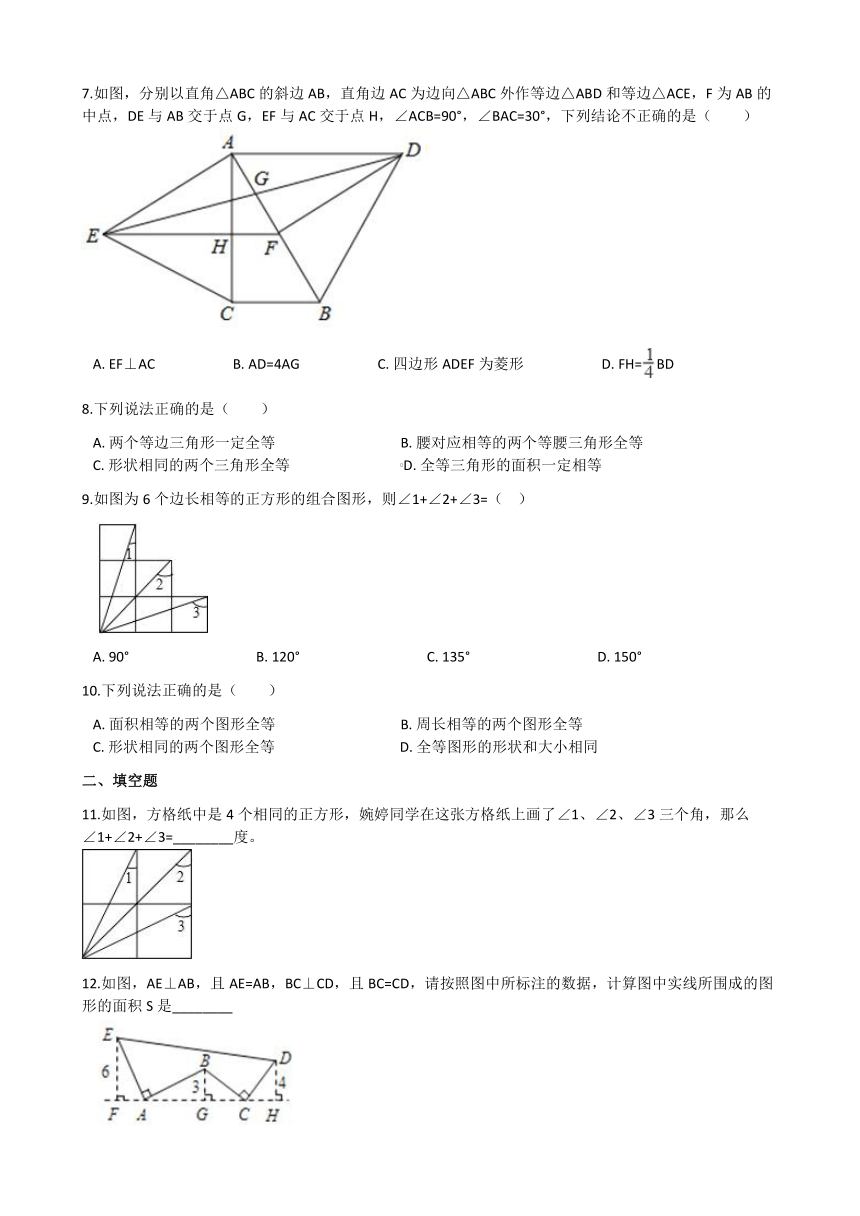
7.如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°，下列结论不正确的是（　　）
A. EF⊥AC B. AD=4AG C. 四边形ADEF为菱形 D. FH=BD
8.下列说法正确的是（　　）
A. 两个等边三角形一定全等 B. 腰对应相等的两个等腰三角形全等
C. 形状相同的两个三角形全等 D. 全等三角形的面积一定相等
9.如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（ ）
A. 90° B. 120° C. 135° D. 150°
10.下列说法正确的是（　　）
A. 面积相等的两个图形全等 B. 周长相等的两个图形全等
C. 形状相同的两个图形全等 D. 全等图形的形状和大小相同
二、填空题
11.如图，方格纸中是4个相同的正方形，婉婷同学在这张方格纸上画了∠1、∠2、∠3三个角，那么∠1+∠2+∠3=________度。
12.如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是________
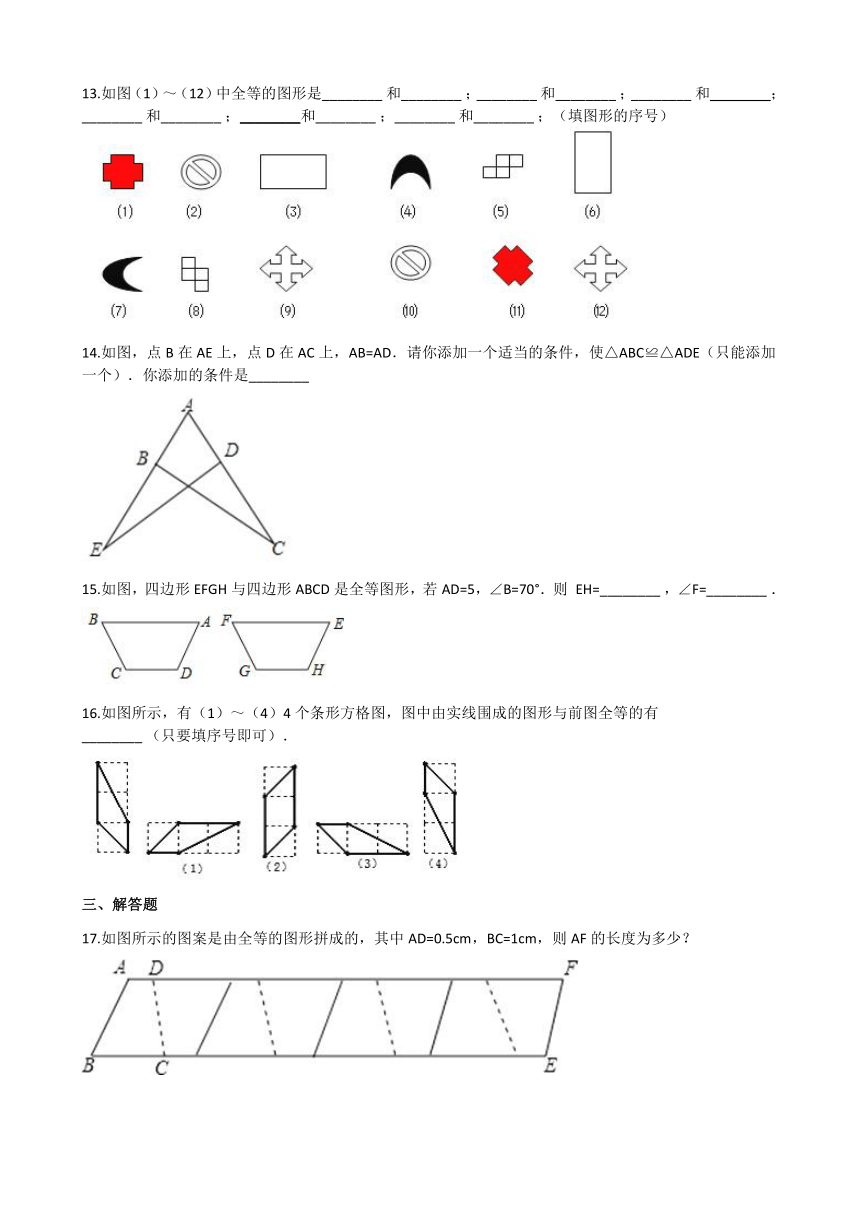
13.如图（1）～（12）中全等的图形是________ 和________ ；________ 和________ ；________ 和________；________ 和________ ；________和________ ；________ 和________ ；（填图形的序号）
14.如图，点B在AE上，点D在AC上，AB=AD．请你添加一个适当的条件，使△ABC≌△ADE（只能添加一个）．你添加的条件是________
15.如图，四边形EFGH与四边形ABCD是全等图形，若AD=5，∠B=70°．则 EH=________ ，∠F=________ ．
16.如图所示，有（1）～（4）4个条形方格图，图中由实线围成的图形与前图全等的有
________ （只要填序号即可）．
三、解答题
17.如图所示的图案是由全等的图形拼成的，其中AD=0.5cm，BC=1cm，则AF的长度为多少？
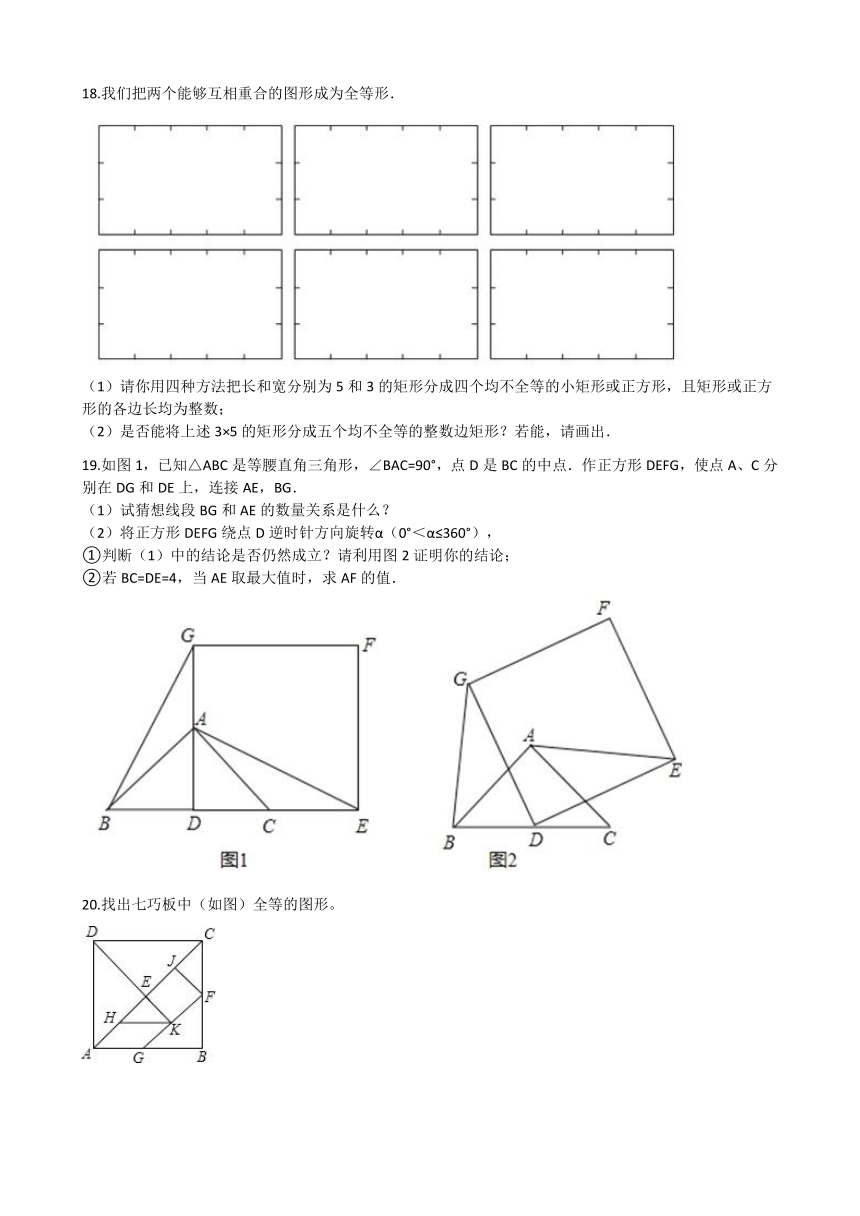
18.我们把两个能够互相重合的图形成为全等形．

（1）请你用四种方法把长和宽分别为5和3的矩形分成四个均不全等的小矩形或正方形，且矩形或正方形的各边长均为整数；
（2）是否能将上述3×5的矩形分成五个均不全等的整数边矩形？若能，请画出．
19.如图1，已知△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点．作正方形DEFG，使点A、C分别在DG和DE上，连接AE，BG．
（1）试猜想线段BG和AE的数量关系是什么？
（2）将正方形DEFG绕点D逆时针方向旋转α（0°＜α≤360°），
①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；
②若BC=DE=4，当AE取最大值时，求AF的值．
20.找出七巧板中（如图）全等的图形。
答案解析部分
一、单选题
1.【答案】D
【解析】【解答】解：A、所有的等边三角形都是全等三角形，错误；
B、全等三角形是指面积相等的三角形，错误；
C、周长相等的三角形是全等三角形，错误；
D、全等三角形是指形状相同大小相等的三角形，正确．
故选：D．
【分析】直接利用全等图形的定义与性质分析得出答案．
2.【答案】D
【解析】【解答】解：A、全等三角形对应角相等，说法正确；
B、全等三角形对应边相等，说法正确；
C、全等三角形的面积相等，说法正确；
D、面积相等的两个三角形一定全等，说法错误，例如一边长为6，这边上的高为3和一边长为3，这边上的高为6的两个三角形，面积相等，却不全等；
故选：D．
【分析】根据全等三角形的性质：全等三角形对应边、对应角相等，能够完全重合的两个三角形叫做全等三角形，进行分析即可．
3.【答案】B
【解析】【解答】①两个图形全等，它们的形状相同，正确；②两个图形全等，它们的大小相同，正确；
③面积相等的两个图形全等，错误；
④周长相等的两个图形全等，错误．
所以只有2个正确，
故答案为：B。
【分析】能够完全重合的两个图形叫做全等形．强调能够完全重合，对选择项进行验证可得答案．
4.【答案】B
【解析】【解答】解：由题意知真正合同三角形和镜面合同三角形的特点，可判断要使选项B的两个三角形重合必须将其中的一个翻转180°；
而其A、D、C的全等三角形可以在平面内通过平移或旋转使它们重合．
故选B．
【分析】认真阅读题目，理解真正合同三角形和镜面合同三角形的定义，然后根据各自的定义或特点进行解答．
5.【答案】C
【解析】【解答】解：A、全等三角形不仅仅形状相同而且大小相同，错；
B、全等三角形不仅仅面积相等而且要边、角完全相同，错；
C、全等则重合，重合则周长与面积分别相等，则C正确．
D、完全相同的等边三角形才是全等三角形，错．
故选C．
【分析】能够完全重合的两个图形叫做全等形．做题时严格按定义逐个验证．全等形的面积和周长相等．
6.【答案】C
【解析】【解答】A、形状相同的两个三角形全等，说法错误，应该是形状相同且大小也相同的两个三角形全等；B、面积相等的两个三角形全等，说法错误；
C、完全重合的两个三角形全等，说法正确；
D、所有的等边三角形全等，说法错误；
故选：C．
【分析】根据全等形的概念：能够完全重合的两个图形叫做全等形，以及全等三角形的判定定理可得答案．
7.【答案】C
【解析】【解答】解：∵△ACE是等边三角形，
∴∠EAC=60°，AE=AC，
∵∠BAC=30°，
∴∠FAE=∠ACB=90°，AB=2BC，
∵F为AB的中点，
∴AB=2AF，
∴BC=AF，
∴△ABC≌△EFA，
∴FE=AB，
∴∠AEF=∠BAC=30°，
∴EF⊥AC，故A正确；
∵EF⊥AC，∠ACB=90°，
∴HF∥BC，
∵F是AB的中点，
∴HF=BC，
∵BC=AB，AB=BD，
∴HF=BD，故D说法正确；
∵AD=BD，BF=AF，
∴∠DFB=90°，∠BDF=30°，
∵∠FAE=∠BAC+∠CAE=90°，
∴∠DFB=∠EAF，
∵EF⊥AC，
∴∠AEF=30°，
∴∠BDF=∠AEF，
∴△DBF≌△EFA（AAS），
∴AE=DF，
∵FE=AB，
∴四边形ADFE为平行四边形，
∵AE≠EF，
∴四边形ADFE不是菱形；
故C说法不正确；
∴AG=AF，
∴AG=AB，
∵AD=AB，
则AD=4AG，故B说法正确，
故选C．
【分析】根据已知先判断△ABC≌△EFA，则∠AEF=∠BAC，得出EF⊥AC，由等边三角形的性质得出∠BDF=30°，从而证得△DBF≌△EFA，则AE=DF，再由FE=AB，得出四边形ADFE为平行四边形而不是菱形，根据平行四边形的性质得出AD=4AG，从而得到答案．
8.【答案】D
【解析】【解答】解：两个等边三角形边长不一定相等，所以不一定全等，A错误；
腰对应相等的两个等腰三角形对应角不一定相等，所以不一定全等，B错误；
形状相同的两个三角形对应边不一定相等，所以不一定全等，C错误；
全等三角形的面积一定相等，所以D正确，
故选：D．
【分析】根据全等图形的判定和性质对各个选项进行判断即可．
9.【答案】C
【解析】【解答】解：如图，在△ABC和△DEA中， ，
∴△ABC≌△DEA（SAS），
∴∠1=∠4，
∵∠3+∠4=90°，
∴∠1+∠3=90°，
又∵∠2=45°，
∴∠1+∠2+∠3=90°+45°=135°．
故答案为：C．
【分析】标注字母，利用“边角边”判断出△ABC和△DEA全等，根据全等三角形对应角相等可得∠1=∠4，然后求出∠1+∠3=90°，再判断出∠2=45°，然后计算即可得解．
10.【答案】D
【解析】【解答】解：A、面积相等的两个图形全等，说法错误；
B、周长相等的两个图形全等，说法错误；
C、形状相同的两个图形全等，说法错误；
D、全等图形的形状和大小相同，说法正确；
故选：D．
【分析】根据等形的概念：能够完全重合的两个图形叫做全等形进行分析即可．
二、填空题
11.【答案】135
【解析】【解答】解：由题意可知△ABC≌△EDC，
∴∠3=∠BAC，
又∵∠1+∠BAC=90°，
∴∠1+∠3=90°，
∵DF=DC，
∴∠2=45°，
∴∠1+∠2+∠3=135度，
故答案为：135。
【分析】根据△ABC≌△EDC得到∠3=∠BAC，求出∠1+∠3=90°，根据等腰直角三角形的性质得到∠2=45°，计算即可．
12.【答案】50
【解析】【解答】解：∵AE⊥AB且AE=AB，EF⊥FH，BG⊥FH ∠FED=∠EFA=∠BGA=90°，
∠EAF+∠BAG=90°，∠ABG+∠BAG=90° ∠EAF=∠ABG，
∴AE=AB，∠EFA=∠AGB，∠EAF=∠ABG △EFA≌△ABG
∴AF=BG，AG=EF．
同理证得△BGC≌△DHC得GC=DH，CH=BG．
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=（6+4）×16﹣3×4﹣6×3=50．
故答案为50．
【分析】由AE⊥AB，EF⊥FH，BG⊥AG，可以得到∠EAF=∠ABG，而AE=AB，∠EFA=∠AGB，由此可以证明 △EFA≌△ABG，所以AF=BG，AG=EF；同理证得△BGC≌△DHC，GC=DH，CH=BG，故 FH=FA+AG+GC+CH=3+6+4+3=16，然后利用面积的割补法和面积公式即可求出图形的面积．
13.【答案】（1）；（11）；（2）；（10）；（3）；（6）；（4）；（7）；（5）；（8）；（9）；（12）
【解析】【解答】解：全等图形是（1）和（11）；（2）和（10）；（3）和（6）；（4）和（7）；（5）和（8）；（9）和（12）．
【分析】根据能够互相重合的两个图形叫做全等图形解答．
14.【答案】AE=AC
【解析】【解答】解：添加条件：AE=AC，
∵在△ABC和△ADE中，
∴△ADE≌△ABC（SAS），
故答案为：AE=AC．
【分析】添加条件：AE=AC，再加上公共角∠A，可利用SAS定理进行判定．
15.【答案】5；70°
【解析】【解答】解：∵四边形EFGH与四边形ABCD是全等图形，AD=5，∠B=70°，
∴EH=AD=5，∠F=∠B=70°，
故答案为：5，70°．
【分析】根据全等图形的性质对应角相等对应边相等进而得出答案．
16.【答案】（1）、（3）、（4）
【解析】【解答】解：设每个小方格的边长为1，则前图的各边长分别为：，1，，2；
（1）的各边长分别是：，1，，2；
（2）的各边长分别是：2，，2，；
（3）的各边长分别是：，1，，2；
（4）的各边长分别是：，1，，2；
由图形知（1）（3）（4）与原图形的角度是对于相等的；
所以与前图全等的有：（1）、（3）、（4）．
故填：（1）、（3）、（4）．
【分析】观察图形，其中（1）（3）（4）各图形的角度与原图形是对于相等的只要边长相等即可重合，于是设每个小方格的边长为1，分别表示出第个图形的各边长，再根据全等形是可以完全重合的图形进行判定即可．
三、解答题
17.【答案】解：由题可知，图中有8个全等的梯形，所以AF=4AD+4BC=4×0.5+4×1=6cm
【解析】【分析】由图形知，所示的图案是由梯形ABCD和七个与它全等的梯形拼接而成，根据全等则重合的性质有AF=4AD+4BC=4×0.5+4×1=6cm．
18.【答案】
解：（1）所画图形如上．
（2）能，所画图形如上所示．
【解析】【分析】（1）根据题意画出图形即可，注意所得的图形不应全等．
（2）作长为1，宽分别为1，2，3，4，5的图形即可．
19.【答案】解：（1）BG=AE．
理由：如图1，∵△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，
∴AD⊥BC，BD=CD，
∴∠ADB=∠ADC=90°．
∵四边形DEFG是正方形，
∴DE=DG．
在△BDG和△ADE中，
，
∴△ADE≌△BDG（SAS），
∴BG=AE．
故答案为：BG=AE；
（2）①成立BG=AE．
理由：如图2，连接AD，
∵在Rt△BAC中，D为斜边BC中点，
∴AD=BD，AD⊥BC，
∴∠ADG+∠GDB=90°．
∵四边形EFGD为正方形，
∴DE=DG，且∠GDE=90°，
∴∠ADG+∠ADE=90°，
∴∠BDG=∠ADE．
在△BDG和△ADE中，
，
∴△BDG≌△ADE（SAS），
∴BG=AE；
②∵BG=AE，
∴当BG取得最大值时，AE取得最大值．
如图3，当旋转角为270°时，BG=AE．
∵BC=DE=4，
∴BG=2+4=6．
∴AE=6．
在Rt△AEF中，由勾股定理，得
AF==，
∴AF=2．
【解析】【分析】（1）由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论；
（2）①如图2，连接AD，由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论；
②由①可知BG=AE，当BG取得最大值时，AE取得最大值，由勾股定理就可以得出结论．
20.【答案】解：由图知：△ADE与△DEC，△EHK与△CJF，△ADC与△ABC，四边形AGKE与四边形CFKE，四边形AGKD与四边形CFKD是重合的，即是全等的图形
【解析】【分析】全等的图形包括全等三角形和全等的四边形，三i角形有3对，四边形有2对.